Here are the classes, structs, unions and interfaces with brief descriptions:
[detail level 123]
| ►NCH_Matrix_Classes | Matrix Classes and Linear Algebra. See Matrix Classes (namespace CH_Matrix_Classes) for a quick introduction |
| CIndexmatrix | Matrix class for integral values of type Integer |
| CIterativeSolverObject | Abstract interface to iterative methods for solving Ax=b given by an IterativeSystemObject |
| CIterativeSystemObject | Abstract base class for supplying the system for an iterative solver |
| CLanczMaxEig | A Lanczos method allowing spectral transformation by Chebycheff polynomials and premature termination |
| CLanczos | Abstract interface to Lanzcos methods for computing a few extremal eigenvalues given via a Lanczosmatrix |
| CLanczosmatrix | Abstract base class for supplying the input matrix for Lanzcosmethods |
| CLanczpol | A Lanczos method allowing spectral transformation by Chebycheff polynomials and premature termination |
| Cmat_greater_index | "greater"-routine for sorting indices of value arrays by std::sort |
| Cmat_less_index | "less"-routine for sorting indices of value arrays by std::sort |
| CMatrix | Matrix class for real values of type Real |
| CMatrixError | Such an object is generated and passed to MEmessage(), whenever an error occurs. It holds some output information on the error |
| CMEdim | Such an object is generated and passed to MEmessage() whenever matrix dimensions do not agree for a desired operation |
| ►CMemarray | A simple memory manager for frequent allocation and deallocation of arrays of roughly the same size |
| CEntry | Holds the information of one allocated block and serves as an item in the singly linked lists |
| CMemarrayuser | All derived classes share a common Memarray memory manager, which is generated with the first user and destructed when the last user is destructed |
| CMEmem | Such an object is generated and passed to MEmessage() whenever a memory allocation fails |
| CMErange | Such an object is generated and passed to MEmessage() whenever some index is out of range |
| CMinRes | MinRes method for solving Ax=b with symmetric (indefinite) matrix A and positive definite preconditioner M1 where the preconditioned system is A'x'=b' with A'=M1^{-.5}AM1^{-.5}, x'=M1^{.5}*x and b'=M1^{-.5}b. System matrix and preconditioner are provided by a CH_Matrix_Classes::IterativeSystemObject |
| CPCG | Preconditioned Conjugate Gradient method for solving Ax=b with (symmetric) positive definite matrix A and positive definite preconditioner M1 where the preconditioned system is A'x'=b' with A'=M1^{-.5}AM1^{-.5}, x'=M1^{.5}*x and b'=M1^{-.5}b. System matrix and preconditioner are provided by a CH_Matrix_Classes::IterativeSystemObject |
| CPsqmr | PSQMR method for solving Ax=b with symmetric matrix A and symmetric preconditioner M=M1*M2 (M1 and M2 regular) where the preconditioned system is A'x'=b' with A'=M1^{-1}AM2^{-1}, x'=M2*x and b'=M1^{-1}b. System matrix and preconditioners are provided by a CH_Matrix_Classes::IterativeSystemObject |
| CRange | Allows to specify a range of integral values via (from, to, step) meaning {j=from+i*step:j in[from,to],i in {0,1,2,...}} |
| CRealrange | Allows to specify a range of real values via (from, to, step,tol) meaning {x=from+i*step:x in(from-tol,to+tol),i in {0,1,2,...}} |
| CSparsemat | Matrix class of sparse matrices with real values of type Real |
| CSparsesym | Matrix class of symmetric matrices with real values of type Real |
| CSymmatrix | Matrix class of symmetric matrices with real values of type Real |
| ►NCH_Tools | Some convenient inline tools like a clock for timing, a random number generator, a heapsort template sorting indices |
| CBoxPlot | For generating LaTeX figures with successive box plots and corresponding tables |
| CClock | Allows measuring time difference to its initialization time in Microseconds |
| CGB_rand | Device independent random number generator based on long int with seed |
| CMicroseconds | Extra long integer number for expressing and computing time measurements in microseconds |
| ►NConicBundle | Conic bundle method solver for sum of convex functions. See the ConicBundle_Manual for a quick introduction |
| CAffineFunctionTransformation | Transform a function f(z) to fun_coeff*f(arg_offset+arg_trafo*y)+linear_cost*y+fun_offset (scales the value, substitutes argument z=c+Ay, and adds an affine term b'y+d) |
| CAFTData | Specialized BundleData class for use with AFTModel for storing and managing essential data of evaluations and the bundle describing the model |
| CAFTModel | Mimicks the model of a function with an AffineFunctionTransformation (AFT) applied to it. It does so by the chain rule and calling the original model of the function |
| CAFTModification | Collects modifications for an AffineFunctionTransformation for the scaling and offset constants as well as for appending, deleting or reassigning columns and rows of the transformation data |
| CBigmatrix | AffineMatrixFunction needs to compute the maximum eigenvalue of an affine matrix function 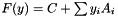 . This class prepares . This class prepares 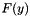 in useful form for iterative eigenvalue solvers in useful form for iterative eigenvalue solvers |
| CBlockPSCPrimal | Implements a block diagonal PSCPrimal consisting of several PSCPrimal blocks |
| CBoxData | Extends BundleData for use with BoxModel by adding information on subgradients and the cutting plane model |
| CBoxIPBundleBlock | QPBundleBlock interface for the interior point routines specific to the primal dual complementarity conditions of a scaled, fulldimensional box given by vectors lb < ub. It resolves the scaling internally. There is no pure QPBlock version of this |
| CBoxModel | Implements (as a derived class of ConeModel) a standard cutting plane model for a MatrixBoxOracle |
| CBoxModelParameters | Abstract interface for BoxModel for the model selection routine |
| CBoxModelParametersObject | Abstract interface for BoxModel for the model selection routine select_model() |
| CBoxOracle | Oracle interface providing the lower and upper bounds for the internally implemented support function over this box for an affine function given by an AffineFucntionTransfomation or, equivalently, Lagrangian relaxation of linear programs over box domains. No modifications of the box groundset are supported so far |
| CBoxPrimalExtender | Interface for extending PrimalData, e.g., in Lagrangian relaxation of column generation approaches |
| CBundleData | Base class for use with SumBlockModel for storing and managing essential data of evaluations and the bundle describing the model |
| CBundleDenseTrustRegionProx | Implements the abstract interface ConicBundle::BundleProxObject for 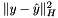 for general symmetric H+weight*I (H is assumed to be positive semidefinite without checking) giving rise to an augmented model with dense variable metric for general symmetric H+weight*I (H is assumed to be positive semidefinite without checking) giving rise to an augmented model with dense variable metric |
| CBundleDiagonalTrustRegionProx | Implements the abstract interface ConicBundle::BundleProxObject for 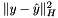 with H=D+weight*I, where D is a diagonal matrix, giving rise to an augmented model with diagonal scaling with H=D+weight*I, where D is a diagonal matrix, giving rise to an augmented model with diagonal scaling |
| CBundleDLRTrustRegionProx | Implements the abstract interface ConicBundle::BundleProxObject for 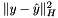 with with 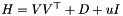 , i.e., a low rank representation of a symmetric positive definite matrix with a diagonal and the weight times identity added as regularization , i.e., a low rank representation of a symmetric positive definite matrix with a diagonal and the weight times identity added as regularization |
| CBundleHKWeight | Routine for selecting the weight of the quadratic/proximal term withing BundleSolver implementing BundleWeight along the paper by Helmberg and Kiwiel |
| CBundleIdProx | Implements the abstract interface ConicBundle::BundleProxObject for 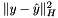 with H=weight*I, giving rise to a pure augmented model without scaling with H=weight*I, giving rise to a pure augmented model without scaling |
| CBundleLowRankTrustRegionProx | Implements the abstract interface BundleProxObject for 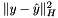 with with 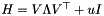 , i.e., a low rank representation of a symmetric positive definite matrix with the weight times identity added as regularization , i.e., a low rank representation of a symmetric positive definite matrix with the weight times identity added as regularization |
| CBundleModel | Abstract interface for BundleSolver giving access to all objective function specific bundle routines and model descriptions. In particular it hides the cutting model and the oracle |
| CBundleParameters | Serves for specifying parameters regarding the construction of cutting models |
| CBundleProxObject | Abstract interface that allows to use different 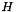 -norms -norms 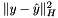 with a positive definite matrix with a positive definite matrix 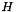 in the proximal term of the augmented model of ConicBundle::BundleSolver in the proximal term of the augmented model of ConicBundle::BundleSolver |
| CBundleRQBWeight | Routine for selecting the weight of the quadratic/proximal term within BundleSolver implementing BundleWeight roughly along the paper C. Lemarechal, C. Sagastizabal, Variable metric bundle methods: From conceptual to implementable forms, Mathematical Programming 76 (1997) 393-410. Implemented obeserving details of the email communication with Claudia Sagastizabal |
| CBundleSolver | This is the internal bundle solver managing descent/null steps with inner updates for approximating the proximal point by alternatingly adapting the groundset aggregate and the model aggregate |
| CBundleTerminator | Basic class implementing termination criteria for BundleSolver, may also serve as base class for other termination criteria |
| CBundleTerminatorData | Abstract interface for BundleTerminator providing the data needed for deciding on termination |
| CBundleWeight | Abstract interface for BundleSolver providing routines that determine the weight of the quadratic term in the augmented model. It also allows the user to specify bounds on the weights by setting minweight and maxweight or to choose the weight to be used in the next iteration |
| CCBout | Base class for uniform use of WARNINGS and ERRORS (at some point in time) |
| CCBSolver | Bundle method solver |
| CCFunction | For the "C" interface this maps c oracles to the standard function oracle with matrix classes |
| CCFunctionMinorantExtender | MinorantExtender for CFunction |
| CCMgramdense | Implements a Gram matrix 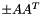 as Coeffmat for a dense rectangular CH_Matrix_Classes::Matrix as Coeffmat for a dense rectangular CH_Matrix_Classes::Matrix 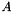 (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) |
| CCMgramsparse | Implements a Gram matrix 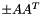 as Coeffmat for a sparse rectangular CH_Matrix_Classes::Sparsemat as Coeffmat for a sparse rectangular CH_Matrix_Classes::Sparsemat 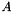 (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) |
| CCMgramsparse_withoutdiag | Implements a Gram matrix 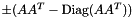 with zero diagonal as Coeffmat for a sparse rectangular CH_Matrix_Classes::Sparsemat with zero diagonal as Coeffmat for a sparse rectangular CH_Matrix_Classes::Sparsemat 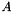 (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) |
| CCMIName | Extends CoeffmatInfo to store a name (e.g. of the constraint it represents) |
| CCMlowrankdd | Implements a low rank matrix 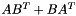 as Coeffmat with as Coeffmat with  each a dense rectangular CH_Matrix_Classes::Matrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) each a dense rectangular CH_Matrix_Classes::Matrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) |
| CCMlowranksd | Implements a low rank matrix 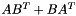 as Coeffmat with as Coeffmat with 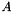 a sparse rectangular CH_Matrix_Classes::Sparsemat and a sparse rectangular CH_Matrix_Classes::Sparsemat and 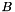 a dense rectangular CH_Matrix_Classes::Matrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) a dense rectangular CH_Matrix_Classes::Matrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) |
| CCMlowrankss | Implements a low rank matrix 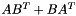 as Coeffmat with as Coeffmat with 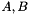 each a sparse rectangular CH_Matrix_Classes::Sparsemat (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) each a sparse rectangular CH_Matrix_Classes::Sparsemat (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) |
| CCMsingleton | Implements a Coeffmat having just one nonzero element (or two by symmetry) for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction) |
| CCMsymdense | Implements a general dense symmetric Coeffmat based on CH_Matrix_Classes::Symmatrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) |
| CCMsymsparse | Implements a general sparse symmetric Coeffmat based on CH_Matrix_Classes::Sparsesym (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)) |
| CCoeffmat | Defines a base class for coefficient matrices in semidefinite programming, in particular for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction) |
| CCoeffmatInfo | Allows to memorize the scalings applied to a Coeffmat and offers the basis for storing further user defined informations on a Coeffmat |
| CCoeffmatPointer | Pointer class for Coeffmat for deleting objects on the heap if Coefmat::use_cnt is reduced to zero and deletion is allowed |
| CConeModel | General abstract base class for conic cutting models with SumBundle capabilities (as a derived class of SumBlockModel) |
| CDensePSCPrimal | Implements a general purpose dense symmetric PSCPrimal based on CH_Matrix_Classes::Symmatrix |
| CFunctionObject | Basic function object (abstract class). It serves for using the same interface on distinct oracle types, but is not yet needed in the standard C++ interface |
| CFunctionObjectModification | Abstract interface for informing the bundle model routines about changes in the oracle function and, possibly, for modifying the affine transformation of the oracle function's arguments |
| CFunctionOracle | Oracle interface (abstract class). For each of your functions, provide a derived class |
| CGramSparsePSCPrimal | PSCPrimal as the sum 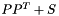 of a Gram matrix and a sparse symmetric matrix of a Gram matrix and a sparse symmetric matrix 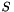 |
| CGroundset | Abstract representation of the feasible convex ground set to be optimized over, provides the QP solver for the bundle subproblem as well as routines for computing feasible points and ground set aggregates |
| CGroundsetModification | Collects modifications for the unconstrained Groundset for appending, deleting or reassigning variables |
| CInteriorPointBlock | Abstract interface for interior point vector/matrix variables and routines specific to primal dual complementarity conditions of symmetric cones |
| CInteriorPointBundleBlock | Abstract interface for interior point routines specific to primal dual complementarity conditions of a symmetric cone with special routines for handling the bundle and the trace constraint |
| CLPGroundset | Polyhedral feasible ground set by affine constraints as in Linear Programming with special support for simple box constraints |
| CLPGroundsetModification | Collects modifications for the linearly constrained LPGroundset for appending, deleting or reassigning variables (with bounds and starting values) and constraints (with bounds) |
| CMatrixCBSolver | The Full Conic Bundle method solver invoked by ConicBundle::MatrixCBSolver(), it uses a separate cutting model for each function |
| CMatrixFunctionOracle | Oracle interface (abstract class). For each of your functions, provide an instance of a derived class |
| CMatrixMinorant | Minorant interface supporting Matrix classes; simple constructros for subgradients given by column vectors in form of a CH_Matrix_Classes::Matrix or a CH_Matrix_Classes::Sparsemat |
| CMinorant | This is used to describe affine minorants of convex functions that will be used for generating cutting models of these functions |
| CMinorantExtender | Interface for extending a Minorant, e.g., in Lagrangian Relaxation of cutting plane approaches |
| CMinorantPointer | Points to MinorantUseData that may be shared by many and allows computations with Minorants |
| CMinorantUseData | Stores use information for the model that the minorant is generated for or to the data the model refers to |
| CModifiableOracleObject | ModifiableOracle provides all oracles with a uniform interface for a modification routine and an on/off switch for internal correctness checks |
| CModification | Base class for collecting and organizing a sequence of changes to linear data so that it can be carried out in one step later on; this class comprises all features, derived ones are specializations with partial reinterpretations |
| CModificationBase | Basic routines for the base classes for reorganizing maps |
| CModificationTreeData | Represents a tree node of the tree within MatrixCBSolver that describes the problem with its interacting functions and that allows to collect modifications before executing them on the respective models |
| CNNCBoxSupportFunction | General purpose implementation of MatrixFunctionOracle as explained in implemention of MatrixFunctionOracle (NNCBoxSupportFunction) (see, however, the likely better choice of a BoxOracle) |
| CNNCBoxSupportMinorantExtender | Implementation of MinorantExtender for NNCBoxSupportFunction |
| CNNCBoxSupportModification | Collects modifications for NNCBoxSupport for appending, deleting or reassigning variables and respective upper and lower bounds |
| CNNCData | Extends BundleData for use with FunctionModel by adding information on subgradients and the cutting plane model |
| CNNCIPBlock | Interface for the interior point variable vector and routines specific to the primal dual complementarity conditions of the nonnegative cone |
| CNNCIPBundleBlock | Interior point variables and routines specific to primal dual complementarity conditions of a nonnegative cone with special routines for handling the bundle and the trace constraint |
| CNNCModel | Implements (as a derived class of SumBlockModel) a standard cutting plane model for a MatrixFunctionOracle |
| CNNCModelParameters | Default model selection routines for NNCModel |
| CNNCModelParametersObject | Abstract interface for NNCModel for the model selection routine select_model() |
| COracleModification | Base class for informing oracles (or the solver) about dynamic changes in the number and sorting of the variables, if such changes occur at all |
| CPrimalData | In Lagrangean relaxation an approximate primal solution can be generated by supplying primal information derived from this abstract class for each epsilon subgradient within ConicBundle::FunctionOracle::evaluate() |
| CPrimalDVector | If in Lagrangean relaxation primal solutions are in the form of a ConicBundle::DVector, then an approximate primal solution can be generated by supplying primal information of this form for each epsilon subgradient within ConicBundle::FunctionOracle::evaluate() |
| CPrimalExtender | Interface for extending PrimalData, e.g., in Lagrangian relaxation of column generation approaches |
| CPrimalMatrix | If in Lagrangean relaxation primal solutions are in the form of a real vector or, more generally a matrix, then an approximate primal solution can be generated by supplying primal information of this form for each epsilon subgradient within ConicBundle::MatrixFunctionOracle::evaluate() |
| CPSCAffineFunction | General purpose implementation of PSCOracle as explained in implemention of a PSCOracle (PSCAffineFunction) |
| CPSCAffineMinorantExtender | Implementation of MinorantExtender for PSCAffineFunction |
| CPSCAffineModification | Class for collecting and organizing a sequence of changes to block diagonal symmetric affine matrix functions so that it can be carried out in one step later on; |
| CPSCBundleParameters | Bundle parameters for PSCModel, we recommend no to modify them |
| CPSCData | Extends BundleData for use with PSCModel (see there for the description of the function) by adding information on Ritz_vectors generating the subgradients and the cutting model |
| CPSCIPBlock | Interface for interior point variable and routines specific to primal dual complementarity conditions of a positive semidefinite cone |
| CPSCIPBundleBlock | Interior point variables and routines specific to the primal dual complementarity conditions of a positive semidefinite cone with special routines for handling the bundle and the trace constraint |
| ►CPSCModel | Implements (as a derived class of ConeModel) a cutting model for a PSCOracle |
| CQPPSCOracleData | For passing oracle information to the QP Solver, which might be used there or not |
| CPSCModelParameters | Default model selection routine for PSCModel |
| CPSCModelParametersObject | Abstract interface for PSCModel for the model selection routine select_model() |
| CPSCOracle | Oracle interface for minimization of the maximum eigenvalue of an affine matrix function or, equivalently, Lagrangian relaxation of semidefinite programs |
| CPSCPrimal | PSCPrimal is the corresponding positive semidefinite object for PSCOracle like PrimalMatrix for a MatrixFunctionOracle |
| CPSCPrimalExtender | Interface for extending PrimalData, e.g., in Lagrangian relaxation of column generation approaches |
| CPSCVariableMetricSelection | Iplementation of a VariableMetricSelection routine for PSCModel for forming and adding variable metric information to a BundleProxObject |
| CQPCentralPathPoint | Currently not in use, storing the points of the central path might help to restart faster if only the cost terms are modified slightly; an instance of this class stores one such point |
| CQPConeModelBlock | Implements a QPModelBlock for conic cutting models in QPSolver |
| CQPConeModelDataObject | Abstract interface extension of QPModelDataObject to allow uniform generation of tuned quadratic solver model blocks in model forming routines for specializd oracles |
| CQPDirectKKTSolver | Implements a direct KKT Solver variant of QPKKTSolverObject |
| CQPIterativeKKTHAeqSolver | Iterative solver for the reduced symmetric, in general indefinite primal dual KKT System within QPSolverBasicStructures, where only the block H and the equality rows of A remain, the inequalities of A as well as B and C are removed by Schur complements. If there are no equalities in A, PCG may used, but MinRes seems to be more stable |
| CQPIterativeKKTHASolver | Iterative solver for the reduced symmetric, in general indefinite primal dual KKT System within QPSolverBasicStructures, where only H and A blocks remain, B and C are removed by Schur complements. If there is no A, PCG may used |
| CQPIterativeKKTSolver | Iterative solver for the full symmetric, in general indefinite primal dual KKT System within QPSolverBasicStructures |
| CQPKKT_KKTStats | Used for collecting statics in QPKKTSolverComparison: For each bundle subproblem there is a block QPKKT_ProbStats, which holds for each KKT system a block of QPKKT_KKTStats (this), which holds for each solver a block QPKKT_SolverStats |
| CQPKKT_ProbStats | Used for collecting statics in QPKKTSolverComparison: For each bundle subproblem there is a block QPKKT_ProbStats (this), which holds for each KKT system a block of QPKKT_KKTStats, which holds for each solver a block QPKKT_SolverStats |
| CQPKKT_SolverStats | Used for collecting statics in QPKKTSolverComparison: For each bundle subproblem there is a block QPKKT_ProbStats, which holds for each KKT system a block of QPKKT_KKTStats, which holds for each solver a block QPKKT_SolverStats (this) |
| CQPKKTPrecondObject | Abstract Interface for preconditioners to be used with a QPIterativeKKTSolver and a CH_Matrix_Classes::IterativeSolverObject, see Interfaces and Classes for Iterative Solvers like PCG, MINRES and PSQMR. It will depend on the system setup and the solver method which preconditioning routines are called and what requirements the preconditioners have to fulfill. Feasible combinations lie in the responsibility of the caller and are not checked for correctness |
| CQPKKTSolverComparison | This is a pseudosolver designed for producing comparative statistics on the performance of mainly iterative solvers for the interior point KKT systems of QPSolver |
| CQPKKTSolverObject | Abstract class for setting up and solving the primal dual KKT System within QPSolverBasicStructures |
| CQPKKTSubspaceHPrecond | Subspace projection preconditioner for the H-block of the KKT-System assuming that B and C have been Schur complemented into the H-block. For the A-Block, if it is there, the identity is used. If there is no A-block, PCG may be used |
| CQPModelBlock | Combines and provides basic functionalities of QPModelDataObject and QPModelBlockObject, but is still abstract |
| CQPModelBlockObject | Abstract interface for model blocks in the constrained QPSolver |
| CQPModelDataObject | Abstract interface declaring the uniform outer appearance of general cutting models produced by the various models for use in generating the model data so that QP Solvers can provide their own tuned data blocks |
| CQPModelDataPointer | Abstract interface for automatically generating and retrieving the qp blocks with the model data that are needed for specific implementations of the qp solver |
| CQPModelOracleDataObject | Abstract base class for passing additional oracle information to the QP |
| CQPModelPointer | Implementation of the QPModelDataPointer Interface for BundelModel for generating the correct type of blocks for QPSolver and for setting the final block in the solver |
| CQPPSCOracleDataObject | Defines an interface for passing on oracle information to PSCIPBundleBlock |
| ►CQPSolver | QPSolver is the access point for ConicBundle to the internal constrained QP Solver, see Internal QP Solver for linearly constrained groundsets |
| CQPProblemData | This class facilitates switching between original data and preprocessed data that removes fixed variables |
| CQPSolverBasicInterface | Defines the abstract interface for QPSolverBasicStructures that the basic routines there need to access the cost and constraint data; it also defines the interface to QPSolverBasicStructures, how to call those routines and how to retrieve the results |
| CQPSolverBasicStructures | Basic variables and implements basic routines for the primal dual interior point solver interface of QPSolverBasicInterface (see there for the problem description and the switched roles of x and y) except for setting up and solving the primal dual KKT system, which is left to a specialized QPKKTSolverObject provided in QPSolverParameters to allow the exploitation of structural properties in the data. The basic problem description must also still be provided in a derived class that implements the remaining abstract data retrieval functions. The bundle data is made available by deriving this class from QPModelPointer, see Interface for qp solver dependent model descriptions |
| CQPSolverObject | Abstract interface for a QPSolver |
| CQPSolverParameters | Parameters for steering the termination criteria and solution method of the solver |
| CQPSolverParametersObject | In order to pass parameters to a customized QPSolverObject, derive the parameters from this object; no other requirements |
| CQPSolverProxObject | In order to pass a ConicBundle::BundleProxObject, see Quadratic Proximal Terms, to a custzomized QPSolverObject, the prox classes are also derived from this object |
| CQPSumModelBlock | Implements a (virtual) cutting model being built of a (possibly recursive) sum of QPModelBlock cutting model instances for QPSolver |
| CQPSumModelDataObject | Abstract interface extension of QPModelDataObject for use in SumModel where several blocks are concatenated for a common bundle |
| CSOCBundleParameters | Bundle parameters for SOCModel |
| CSOCData | Extends BundleData for use with SOCModel (see there for the description of the function) by adding information on SOC_vectors generating the subgradients and the cutting model |
| CSOCIPBlock | Interface for interior point variable and routines specific to primal dual complementarity conditions of a second order cone |
| CSOCIPBundleBlock | Interior point variables and routines specific to primal dual complementarity conditions of a second order cone with special routines for handling the bundle and the trace constraint |
| CSOCModel | Implements (as a derived class of ConeModel) a cutting model for a SOCOracle |
| CSOCModelParameters | Default model selection routine for SOCModel |
| CSOCModelParametersObject | Abstract interface for SOCModel for the model selection routine select_model() |
| CSOCOracle | Oracle interface for minimization of the support function over the seoncd order cone with 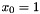 for an affine cost function or, equivalently, Lagrangian relaxation of second order cone programs for an affine cost function or, equivalently, Lagrangian relaxation of second order cone programs |
| CSOCPrimalExtender | Interface for extending PrimalData, e.g., in Lagrangian relaxation of column generation approaches |
| CSOCSupportFunction | General purpose implementation of SOCOracle as explained in implemention of a SOCOracle (SOCSupportFunction) |
| CSOCSupportMinorantExtender | Implementation of MinorantExtender for SOCSupportFunction |
| CSOCSupportModification | Collects modifications for SOCSupportFunction for appending, deleting or reassigning variables |
| CSparseCoeffmatMatrix | Stores/organizes the CoeffmatPointer pointers to Coeffmat matrices with the purpose of describing the block diagonal symmetric matrices used in PSCAffineFunction |
| CSparsePSCPrimal | Implements a sparse symmetric PSCPrimal collecting data only on a sparse, prespecified support; it is based on CH_Matrix_Classes::Sparsesym |
| CSumBlockModel | Abstract interface extending BundleModel so that any such model can be used alone or within SumModel and so that it supports AffineFunctionTransformation as well as switching to a SumBundle with some SumBundleHandler |
| ►CSumBundle | Class for use with SumBlockModel and BundlData for storing and managing a common bundle describing (part of) the model |
| CBData | |
| ►CSumBundleHandler | Routines for updating and handling SumBundle components, possibly by cooperating over several recursive levels |
| CBundleInformation | Allows to store organizational information for each FunctionTask type of bundle |
| CSumBundleParameters | Implements two versions of select_model() (update_rule in {0,1}) |
| CSumBundleParametersObject | Abstract interface for SumBundleHandler for the model selection and variable metric seletcion routines |
| ►CSumModel | Gives a SumBlockModel interface to a sum of (possibly AffineFunctionTransformation transformed) SumBlockModels. This allows e.g. to optimize over a nonnegative combination of convex functions, possibly each with its own cutting model |
| CModelData | For each model added to the sum, there is an object ModelData that stores required information |
| CSumModelParameters | Suggestion procedure for including models in a joint SumBundle model of SumModel |
| CSumModelParametersObject | Abstract interface for SumModel for the models selection routine when using SumBundle and SumBundleHandler |
| CUnconstrainedGroundset | Implements an unconstrained groundset |
| CUQPConeModelBlock | Implements a UQPModelBlock for conic cutting models in UQPSolver |
| CUQPModelBlock | Combines and provides basic functionalities of QPModelDataObject and UQPModelBlockObject, but is still abstract |
| CUQPModelBlockObject | Abstract interface for model blocks in the unconstrained UQPSolver |
| CUQPModelPointer | Interface in BundelSolver for generating the correct type of blocks for UQPSolver and for setting the final block in the solver |
| CUQPSolver | Unconstrained QP solver combining the properties of a QPModelDataPointer and QPSolverObject |
| CUQPSumModelBlock | Implements a (virtual) cutting model being built of a (possibly recursive) sum of UQPModelBlock cutting model instances for UQPSolver |
| CVariableMetric | Interface class that allows a VariableMetricModel to contribute information to a VariableMetric object for use in a BundleProxObject |
| CVariableMetricBundleData | Abstract interface providing the bundle data that is typically needed in VariableMetricSelection classes |
| CVariableMetricModel | Declares the interface that a BundelModel needs to provide for contributing to VariableMetric information |
| CVariableMetricSelection | Abstract interface, that allows to specify a routine for providing or computing a suitable variable metric for specific models. Per current default, no such information is generated |
| CVariableMetricSVDSelection | General implementation of a VariableMetricSelection routine to form and add variable metric information to a BundleProxObject generically mainly from the aggregate and a collection of minorants given by a MinorantBundle |
| CCB_CSolver | Interface class for implementing the language "C" interface |
 1.8.13
1.8.13