abstract interface for model blocks in the unconstrained UQPSolver More...
#include <UQPModelBlockObject.hxx>
Public Member Functions | |
| virtual | ~UQPModelBlockObject () |
| virtual destructor | |
| virtual CH_Matrix_Classes::Integer | xdim () const =0 |
| dimension of externally visible primal variables | |
| virtual CH_Matrix_Classes::Integer | ydim () const =0 |
| dimension of externally visible dual variables | |
| virtual int | set_qp_xstart (CH_Matrix_Classes::Integer x_start_index)=0 |
| the indices of the local variables correspond to the indices of the qp variables x and z starting with this index; returns 0 on success, 1 on failure | |
| virtual int | set_qp_ystart (CH_Matrix_Classes::Integer y_start_index)=0 |
| the indices of the local variables correspond to the indices of the qp variables y starting with this index; returns 0 on success, 1 on failure | |
| virtual int | starting_x (CH_Matrix_Classes::Matrix &qp_x)=0 |
| generate a strictly feasible primal starting point, store it in the qpx_range of x; returns 0 on success, 1 on failure | |
| virtual int | starting_y (CH_Matrix_Classes::Matrix &qp_y, const CH_Matrix_Classes::Matrix &qp_Qx, const CH_Matrix_Classes::Matrix &qp_c)=0 |
| generate a strictly feasible dual starting point, store it in the qpy_range of y, x is fixed already by a previous call to starting_x and Qx=Q*x; returns 0 on success, 1 on failure | |
| virtual CH_Matrix_Classes::Real | get_local_primalcost () const =0 |
| returns the current local primal cost contribution <d,s> | |
| virtual CH_Matrix_Classes::Real | get_local_dualcost () const =0 |
| returns the current local dual cost contribution | |
| virtual int | get_Ab (CH_Matrix_Classes::Matrix &qp_A, CH_Matrix_Classes::Matrix &qp_b) const =0 |
| store the local coefficients of matrices A and b in the positions corresponding to qpy_range (rows) and qpx_range (columns); returns 0 on success, 1 on failure | |
| virtual int | restart_x (CH_Matrix_Classes::Matrix &qp_x, const CH_Matrix_Classes::Matrix &qp_c, const CH_Matrix_Classes::Matrix &qp_dc)=0 |
| it is assumed that the problem was solved already once and is now resolved for a new linear cost term qp_c that resulted from the old one by adding qp_dc. More... | |
| virtual int | restart_y (CH_Matrix_Classes::Matrix &qp_y, const CH_Matrix_Classes::Matrix &qp_Qx, const CH_Matrix_Classes::Matrix &qp_c, const CH_Matrix_Classes::Matrix &qp_dc)=0 |
| this is called after restart_x (see there) More... | |
| virtual int | add_xinv_kron_z (CH_Matrix_Classes::Symmatrix &barQ)=0 |
| add the system term corresponding to (xinv kron z) (that arises from solving the linearized perturbed complementarity system x*z =0 or =mu*I for dx in the preferred search direction) to the diagonal block corresponding to qpx_range x qpx_range | |
| virtual int | add_local_sys (CH_Matrix_Classes::Symmatrix &sysdy, CH_Matrix_Classes::Matrix &rhs)=0 |
| add the local system informatoin More... | |
| virtual int | suggest_mu (CH_Matrix_Classes::Real &ip_xz, CH_Matrix_Classes::Integer &mu_dim, CH_Matrix_Classes::Real &sigma, const CH_Matrix_Classes::Matrix &qp_dx, const CH_Matrix_Classes::Matrix &qp_dy, const CH_Matrix_Classes::Matrix &rhs_residual)=0 |
| supply the information for the choice of the next barrier parameter value More... | |
| virtual int | get_corr (CH_Matrix_Classes::Matrix &xcorr, CH_Matrix_Classes::Matrix &rhs, CH_Matrix_Classes::Real mu)=0 |
| supply the information for the corrector More... | |
| virtual int | line_search (CH_Matrix_Classes::Real &alpha, const CH_Matrix_Classes::Matrix &qp_dx, const CH_Matrix_Classes::Matrix &qp_dy, const CH_Matrix_Classes::Matrix &rhs_residual)=0 |
| perform a line search for the block variables More... | |
| virtual int | set_point (const CH_Matrix_Classes::Matrix &qp_x, const CH_Matrix_Classes::Matrix &qp_y, CH_Matrix_Classes::Real alpha)=0 |
| x,y,z is the new point and has to be stored, alpha is the step size used in the step, it is passed so thatthe block can take the same step for internal variables if needed. | |
| virtual CH_Matrix_Classes::Matrix & | add_Bs (CH_Matrix_Classes::Matrix &qp_vec) const =0 |
| add the local product of matrices B and s in the positions corresponding to qpy_range (rows) and return qp_vec; returns 0 on success, 1 on failure | |
| virtual CH_Matrix_Classes::Matrix & | subtract_z (CH_Matrix_Classes::Matrix &dual_residual, bool with_step=false) const =0 |
| add the contributions of the dual slacks and return dual_residual returns 0 on success, 1 on failure | |
Detailed Description
abstract interface for model blocks in the unconstrained UQPSolver
The UQPSolver solves, for a given positive definite matrix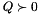 
, line cost vector 
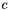and a constant offset 
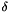the block quadratic program
![\[ \begin{array}{ll} \max & -\frac12\langle Qx,x\rangle +\langle c,x \rangle +\langle d,s\rangle +\delta \\ & A_ix_i + B_is_i = b_i \\ & x_i\in K_{i,1}, s_i\in K_{i,2} \\ & x=(x_i), s=(s_i) \end{array} \qquad \begin{array}{lcll} \min & \frac12\langle Qx,x\rangle &+\langle b,y\rangle&+\delta\\ & Qx &+ A^Ty &- z = c \\ & & B^Ty &- t = d \\ & & &z_i\in K_{i,1}^*, t_i\in K_{i,2}^* \end{array} \]](form_163.png)
The blocks i are completely independent, the main code only works on variables x,y,z, coefficients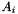 
, and 
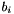. The variables 
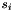and coefficients 
, 
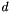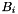are local in each block and have to be treated there (see block definition below). The feasible set of each block has to be full dimensional and compact, each block has to provide a strictly feasible primal-dual starting point, do its line search etc.
In this setting an UQPModelBlockObject corresponds to one block in the quadratic program. It hides the structure of the constraint set and makes visible only the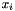 
and the dual variables to the constraints. The block holds a copy of the variables, knows how to find a feasible starting point, computes the step direction, the line search, etc.
An implementation of an UQPModelBlockObject must yield a feasible primal-dual predictor-corrector method with symmetric system matrix, but there are no further restrictions on the choice of the step direction or the step size. the QP_solver below will iteratively go through the steps to to generate the next system matrix, compute a predictor step, collect suggestions for mu, compute a corrector step, find a common step size and move on.
Member Function Documentation
◆ add_local_sys()
|
pure virtual |
add the local system informatoin
on input: sysdy= A*barQ^{-1}*A^T (barQ as returned in add_xinv_kron_z) rhs= A*barQ^{-1}*(c-Q*x-A^T*y)-(b-A*x)
if the block uses additional internal variables (like an additional term + B*s with s>=0 in the primal feasibility constr) then the corresponding block terms have now to be added to sysdy and rhs, eg, sysdy += B*(t^{-1} kron s)*B^T (if t is the dual variable to s) rhs += B*s - B*(t^{-1} kron s)*B^T*y
Implemented in ConicBundle::UQPConeModelBlock, and ConicBundle::UQPSumModelBlock.
◆ get_corr()
|
pure virtual |
supply the information for the corrector
on input (w.r.t. corresponding positions) xcorr = 0 rhs as on output of add_local_sys
on output the corresponding positions of xcorr should hold the corrector term of the search direction, eg, xcorr = mu*x^{-1} - x^{-1}*dx*dz, and if the block holds additional local variables as in add_local_sys then
rhs += B*(mu * t^{-1}- t^{-1}*dt*ds)
has to be called after suggest_mu which computes the other directions
Implemented in ConicBundle::UQPConeModelBlock, and ConicBundle::UQPSumModelBlock.
◆ line_search()
|
pure virtual |
perform a line search for the block variables
dx,dy give the final step direction, alpha is on input an upper bound on the step size.
On output alpha has to be no larger than on input and has to guarantee strict feasibility of the primal/dual step on the local variables.
The block has to compute the step direction dz as well as for additional internal variables now and to choose alpha so that strict feasibility is guaranteed for the internal variables as well
Implemented in ConicBundle::UQPConeModelBlock, and ConicBundle::UQPSumModelBlock.
◆ restart_x()
|
pure virtual |
it is assumed that the problem was solved already once and is now resolved for a new linear cost term qp_c that resulted from the old one by adding qp_dc.
on input qp_x holds the old optimal solution and on output the coorespoind qpx_range should be replaced by a reasonable strictly feasible solution for x suitable for restarting (see also restart_yz)
returns 0 on success, 1 on failure
Implemented in ConicBundle::UQPConeModelBlock, and ConicBundle::UQPSumModelBlock.
◆ restart_y()
|
pure virtual |
this is called after restart_x (see there)
on input qp_y and qp_z hold the old optimal solution and on output the coorespoind qpy/qpx_range should be replaced by a reasonable strictly feasible solution for y/z suitable for restarting
returns 0 on success, 1 on failure
Implemented in ConicBundle::UQPConeModelBlock, and ConicBundle::UQPSumModelBlock.
◆ suggest_mu()
|
pure virtual |
supply the information for the choice of the next barrier parameter value
dx, dy is the predictor direction giving rise to the rhs_residual -(c-At(y+dy)-Q(x+dx)). Compute the direction dz and local step and based on the predictor (x+dx,y+dy,z+dz) suggest a value for mu by specifying the inner product of the dual cone variables ip_xz=ip(x,z)+ip(s,t), the dimension of the conic variable space mu_dim= cone_x.dim+cone_s.dim a value for the factor on mu to obtain the new target
Implemented in ConicBundle::UQPConeModelBlock, and ConicBundle::UQPSumModelBlock.
The documentation for this class was generated from the following file:
