Here is a list of all modules:
| Interface to ConicBundle for the Language C | Solve 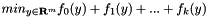 for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here. Internal details are sketched in Internal implementation of the "C" interface for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here. Internal details are sketched in Internal implementation of the "C" interface |
| Interface to ConicBundle for the Language C++ | Solve 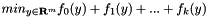 for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here |
| Interface to ConicBundle for the Language C++ using Matrix Classes | Solve 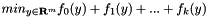 for convex functions f_i, the y-variables may be free, bounded, box constrained, or linearly constrained. The most important steps are the following for convex functions f_i, the y-variables may be free, bounded, box constrained, or linearly constrained. The most important steps are the following |
| Internal implementation of the "C" interface | Internally the "C" interface is implemented as follows. cb_construct_problem() generates a CB_CSolver that contains a MatrixCBSolver and feeds each c-evaluation function to this solver in the form of a CFunction. All calls are then passed on to this solver |
| Basic Support for Output Levels | |
| Interface for qp solver dependent model descriptions | The classes define the interface for obtaining a solver dependent description of the bundle subproblem. The solver has to provide (or be) a QPModelDataPointer, which generates on request (issued in ConicBundle::BundleModel::start_augmodel() ) a possibly model dependent QPModelDataObject that the model then fills with its information. Derived from this base class QPModelDataObject there is QPSumModelDataObject used by ConciBundle::SumModel and QPConeModelDataObject that is general enough to fit the models of ConicBundle::NNCModel, ConicBundle::SOCModel, ConicBundle::PSCModel, ConicBundle::BoxModel, and ConicBundle::AFTModel. The cutting model description typically consists of the collected subgradient information and the support set describing the feasible combinations of the subgradient information. A potentially present sequence of AffineFunctionTransformation instances modifies this subgradient information and the routine QPModelDataPointer::apply_aft() serves this purpose. Several classes derived from BundleProxObject also use this interface to compute the quadratic costs for the internal ConicBundle::UQPSolver |
| Abstract interface for qp solvers | The classes define the interface for qp solvers to be compatible with ConicBundle::UnconstrainedGroundset and ConicBundle::LPGroundset. Solvers obeying these requirements may be installed by ConicBundle::MatrixCBSolver::set_qp_solver() |
| Internal QP Solver for linearly constrained groundsets | |
| Internal QP Solver for unconstrained groundsets | |
| Variable Metric | The classes and routines here help to dynamically specify the part of the quadratic term within the proximal term (see Quadratic Proximal Terms) that is responsible for the shape of the level sets of the prox term in the bundle subproblem. In the smooth case this quadratic contribution should be the Hessian of the function. Generally the term should make it easy to move into directions that are still considered promising and where "curvature" also seems to allow for larger steps |
| Quadratic Proximal Terms | Together with a weight (see BundleWeight), the proximal term 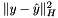 ( ( 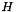 positive definite) of the augmented cutting model plays the role of a step length control and offers a possibility to bring in some metric information via the choice of positive definite) of the augmented cutting model plays the role of a step length control and offers a possibility to bring in some metric information via the choice of 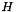 (see Variable Metric). Two aspects are of importance in choosing this matrix (see Variable Metric). Two aspects are of importance in choosing this matrix |
| Classes for Describing Types of Ground Sets and Ensuring Feasibility of y | |
| Internal Bundle Solver of ConicBundle | Solve  for a convex function f given in the form of a ConicBundle::BundleModel. The Problem and the Solver are set up and called from one of the solver interfaces, e.g., ConicBundle::CBSolver or ConicBundle::MatrixCBSolver and are typically not accessed directly for a convex function f given in the form of a ConicBundle::BundleModel. The Problem and the Solver are set up and called from one of the solver interfaces, e.g., ConicBundle::CBSolver or ConicBundle::MatrixCBSolver and are typically not accessed directly |
| dynamic modification support for adding/deleting/modifying variables, oracles and constraints | Most classes are specializations/reinterpretations of the class Modification |
| Classes for General and Specialized Cutting Models for Various Objective Functions | |
| implemention of MatrixFunctionOracle (NNCBoxSupportFunction) | NNCBoxSupportFunction is an example implementation of ConicBundle::MatrixFunctionOracle for the minimization of the support function over a box (it is, however, recommended to use a BoxOracle instead, which should be more efficient). It may be used for Lagrangian relaxation of linear programs over boxes or, using FunctionTask::AdaptivePenaltyFunction, over unbounded domains with finite optima |
| box oracle with special purpose cutting model | This oracle has the only purpose of passing the box description data to a specialized internal implementation of a support function over a box. The objective is supplied by a suitable AffineFunctionTransformation |
| dynamic submodel selection | |
| abstract second order cone oracle | For minimizing the support function over the second order cone with 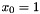 for an affine cost function or, equivalently, Lagrangian relaxation of Linear Programs over the second order cone for an affine cost function or, equivalently, Lagrangian relaxation of Linear Programs over the second order cone |
| implemention of a SOCOracle (SOCSupportFunction) | SOCSupportFunction is an implementation of ConicBundle::SOCOracle for the minimization of the support function over the second order cone with x0=1, which may be used for Lagrangian relaxation of linear programs over the second order cone |
| abstract positive semidefinite cone oracle | For the minimization of the maximum eigenvalue of affine matrix functions (see also implemention of a PSCOracle (PSCAffineFunction)) or, equivalently, Lagrangian relaxation of Linear Programs over the cone of positive semidefinite matrices |
| implemention of a PSCOracle (PSCAffineFunction) | PSCAffineFunction is an implementation of ConicBundle::PSCOracle for the minimization of the maximum eigenvalue of an affine matrix function or, equivalently, Lagrangian relaxation of Linear Programs over the cone of positive semidefinite matrices |
| Basic Types and Constants | |
| Basic Templates for Linear Algebra | Templates for simple linear algebra routines like BLAS level 1 |
| Global Variables and Objects | The variables and objects are instantiated in memarray.cxx |
| Classes and Functions used for Debugging | To catch MatrixErrors in CONICBUNDLE_DEBUG mode stop/break in CH_Matrix_Classes::MEmessage() (first routine in memarray.cxx) |
| Classes and Functions for Memory Management | Implements a simple approach to support frequent allocation and deallocation of arrays of the same sizes |
| simple functions like max, min, abs | |
| Range (of integer numbers with step size) | |
| Friend Functions of Indexmatrix | |
| Indexmatrix (dense, integer, m by n) | |
| Realrange (of real numbers with step size) | |
| Matrix (dense, real, m by n) | |
| Symmatrix (dense, real, symmetric, n by n) | |
| Sparsemat (sparse, real, n by m) | |
| Sparsesym (sparse, real, symmetric, n by n) | |
| Lanczos Interface and Classes | Routines for computing a few extremal eigenvalues of large structured real symmetric matrices |
| Interfaces and Classes for Iterative Solvers like PCG, MINRES and PSQMR | Uniform interface for routines for solving positive definite or indefinite symmetric or unsymmetric systems Ax=b by iterative methods with or without preconditioning. The meaning, the requirements and the use of the preconditioner routines depends on the methods |
| Clock (time measurement in Microseconds) | |
| Random Number Generator | |
| Heapsort | Template functions for heapsorting an array of index-objects indexing an array of value-objects comparable by "<" |
| Plot (output of statistical data with pgfplots) |
 1.8.13
1.8.13