Solve 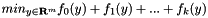 for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here.
More...
for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here.
More...
Classes | |
| class | ConicBundle::PrimalData |
| In Lagrangean relaxation an approximate primal solution can be generated by supplying primal information derived from this abstract class for each epsilon subgradient within ConicBundle::FunctionOracle::evaluate(). More... | |
| class | ConicBundle::PrimalExtender |
| Interface for extending PrimalData, e.g., in Lagrangian relaxation of column generation approaches. More... | |
| class | ConicBundle::FunctionObject |
| basic function object (abstract class). It serves for using the same interface on distinct oracle types, but is not yet needed in the standard C++ interface. More... | |
| class | ConicBundle::Minorant |
| this is used to describe affine minorants of convex functions that will be used for generating cutting models of these functions. More... | |
| class | ConicBundle::MinorantExtender |
| Interface for extending a Minorant, e.g., in Lagrangian Relaxation of cutting plane approaches. More... | |
| class | ConicBundle::OracleModification |
| Base class for informing oracles (or the solver) about dynamic changes in the number and sorting of the variables, if such changes occur at all. More... | |
| class | ConicBundle::PrimalDVector |
| If in Lagrangean relaxation primal solutions are in the form of a ConicBundle::DVector, then an approximate primal solution can be generated by supplying primal information of this form for each epsilon subgradient within ConicBundle::FunctionOracle::evaluate(). More... | |
| class | ConicBundle::FunctionOracle |
| oracle interface (abstract class). For each of your functions, provide a derived class. More... | |
| class | ConicBundle::BundleParameters |
| Serves for specifying parameters regarding the construction of cutting models. More... | |
| class | ConicBundle::CBSolver |
| Bundle method solver. More... | |
Typedefs | |
| typedef std::vector< double > | ConicBundle::DVector |
| A dense vector of double, arguments and subgradients are specified like this. | |
| typedef std::vector< int > | ConicBundle::IVector |
| A dense vector of int, index vectors for deleting/reorganizing variables are specified like this. | |
Enumerations | |
| enum | ConicBundle::FunctionTask { ObjectiveFunction =0, ConstantPenaltyFunction =1, AdaptivePenaltyFunction =2 } |
Each function 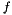 represented by a FunctionModel is equipped with a function_factor represented by a FunctionModel is equipped with a function_factor 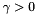 (it defaults to 1.) and may be declared as a usual objective function (default) or as a penalty function (it defaults to 1.) and may be declared as a usual objective function (default) or as a penalty function 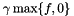 with either a constant penalty factor or an adaptive penalty factor with either a constant penalty factor or an adaptive penalty factor 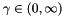 . More... . More... | |
Variables | |
| const double | ConicBundle::CB_plus_infinity |
| serves as the value "minus infinity", i.e., all bounds <= this value are set to this value and are regarded as minus infinity | |
| const double | ConicBundle::CB_minus_infinity |
| serves as the value "plus infinity", i.e., all bounds >= this value are set to this value and are regarded as plus infinity | |
| const double | ConicBundle::CB_minorant_zero_tolerance |
| serves as the default tolerance for considering minorant entries as zero | |
| const double | ConicBundle::CB_minorant_sparsity_ratio |
| serves as the default ratio of nonzeros to dimension for using a sparse representatio of a minorant | |
Detailed Description
Solve 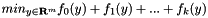 for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here.
for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here.
Setting up the Problem, the Functions, and the Main Loop
First create a new problem/solver ConicBundle::CBSolver, let us call it solver for brevity. In invoking the constructor a boolean flag may be set to enforce the use of a minimal bundle model that employs only one common aggregate and one common subgradient for all functions, so basically "no bundle", which may be favorable if fast iterations and/or little memory consumption are essential.
Next, set the dimension of the design variables/argument as well as possible box constraints on these by ConicBundle::CBSolver::init_problem().
Now set up each of your functions f_i as a ConicBundle::FunctionOracle. Via the routine ConicBundle::FunctionOracle::evaluate() you will supply, for a given argument, the function value and a subgradient (=the gradient if the function is differentiable) to the solver. The function evaluate() is the only function that you definitely have to provide, see the miniature example below.
The function oracles have to be added to the solver using the routine ConicBundle::CBSolver::add_function().
Once all functions are added, the optimization process can be started. If you know a good starting point then set it with ConicBundle::CBSolver::set_new_center_point() now, otherwise the method will pick the zero vector or, in the case of box constraints, the point closest to zero as starting point.
Finally, call ConicBundle::MatrixCBSolver::solve() and retrieve ConicBundle::MatrixCBSolver::termination_code() for getting the reason for termination. Via parameters in solve() you may also tell the solver to return after each descent step or also after a maximum number of null steps. This then only interrupts computations and calling solve() again continues as if there was not break at all.
Setting up the Problem, the Functions, and the Main Loop
After the first call to ConicBundle::CBSolver::solve() you can retrieve, at any time, the current objective value by ConicBundle::CBSolver::get_objval() and the argument leading to this value by ConicBundle::CBSolver::get_center(). For some screen output, use ConicBundle::CBSolver::set_out().
Lagrangean Relaxation, Primal Approximations, and Cutting Planes
If you are optimizing the Lagrange multipliers of a Lagrangean relaxation, you might be interested in getting an approximation to your primal optimal solution. This can be done by specifying in each function for each (epsilon) subgradient the corresponding primal vectors that generate it, see the parameter primal_solutions in ConicBundle::FunctionOracle::evaluate() as a start. Then for each of your functions, you can retrieve the current primal approximation using ConicBundle::CBSolver::get_approximate_primal().
If, in addition, you plan to improve your primal relaxation via cutting planes, that are strongly violated by the current primal approximation, you should have a look at ConicBundle::CBSolver::append_variables(), ConicBundle::FunctionOracle::subgradient_extension() and ConicBundle::CBSolver::reinit_function_model(). If you want to get rid of primal constraints/dual variables, use ConicBundle::CBSolver::get_approximate_slacks() and ConicBundle::CBSolver::delete_variables().
Enumeration Type Documentation
◆ FunctionTask
Each function 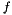 represented by a FunctionModel is equipped with a function_factor
represented by a FunctionModel is equipped with a function_factor 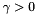 (it defaults to 1.) and may be declared as a usual objective function (default) or as a penalty function
(it defaults to 1.) and may be declared as a usual objective function (default) or as a penalty function 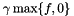 with either a constant penalty factor or an adaptive penalty factor
with either a constant penalty factor or an adaptive penalty factor 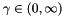 .
.
- Attention
- AdaptivePenaltyFunction is still very experimental and not yet reliable
- ObjectiveFunction adds
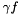
- ConstantPenaltyFunction adds
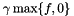
- AdaptivePenaltyFunction adds
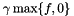 for
for 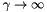 so that the result should resemble the indicator of the level set to level 0 (in exact penalty cases there will be no need to go to infinity)
so that the result should resemble the indicator of the level set to level 0 (in exact penalty cases there will be no need to go to infinity)
 1.8.13
1.8.13