this is used to describe affine minorants of convex functions that will be used for generating cutting models of these functions. More...

#include <CBSolver.hxx>

Inheritance diagram for ConicBundle::Minorant:

Public Member Functions
	Minorant (double offset, const DVector &subg, PrimalData *primal=0, bool offset_at_origin=false)
	Minorant constructor for a dense subgradient specified via a DVector. More...

	Minorant (double offset, const DVector &subg_val, const IVector &subg_ind, PrimalData *primal=0, bool offset_at_origin=false)
	Minorant constructor for a sparse subgradient where the nonzero values are specified by DVector and the corresponding indices by an IVector. More...

	Minorant (bool offset_at_origin=true, double offset=0., int n_elementes=0, const double coeffs=0, const int indices=0, double scale_val=1., PrimalData *primal=0)
	default initializes a zero minorant, see full explanation otherwise; NOTE: if the offset supplied by the minorant refers to the evaluation point (i.e., if it is the function value at the point of evaluation), set offset_at_origin = false ! More...

	Minorant (const Minorant *mnrt, double factor=1., bool with_primal=false)
	they main purpose of this constructor is to allow easy cloning for derived classes

virtual double	offset () const
	returns the current offset value

virtual int	add_offset (double value)
	adds this value to the current offset value

virtual bool &	offset_gives_value_at_origin ()
	allows to specify/modify whether the offset refers to origin or to the point of evaluation at which this minorant was supplied

virtual bool	offset_gives_value_at_origin () const
	true if the offset refers to origin and false, if the offset refers to the value of the minorant in the point of the oracle evaluation at which this minorant was supplied

virtual double	coeff (int i)
	returns the value of the coefficient in coordinate i

virtual int	add_coeff (int i, double value)
	adds the value to the coefficient in coordinate i

virtual int	add_coeffs (int n_elements, const double *values, double factor=1., int start_pos=0)
	adds the n values (possibly multiplied by factor) to consecutive coefficients starting at start_pos (by default 0); this always converts the minroant into a dense vector first and adds then

virtual int	add_coeffs (int n_elements, const double values, const int indices, double factor=1.)
	adds the n values (possibly multiplied by factor) to the coefficients indicated by indices (if zero, this calls the other add_coeffs for the consecutive version)

virtual int	sparsify (double tol=CB_minorant_zero_tolerance, double sparsity_ratio=CB_minorant_sparsity_ratio)
	converts to sparse format with zeros of absolut value at most tol*(fabs(offset)+1) if the given ratio of elements is zero in relation to the maximum nonzero index

virtual int	nonzeros ()
	returns the number of nonzero coefficients

virtual int	get_coeffs (int &n_elements, const double &coeffs, const int &indices) const
	returns the list of all nonzero coefficients by returning pointers to the arrays and their common length n_elements More...

virtual double *	get_dense_coeff_store (int n_elements)
	If the returned pointer is not NULL it gives direct access to the array of current coefficient values with indices 0 up to n_elements-1;. More...

virtual int	reassign_coeffs (int n_elements, const int *map_to_old_coeffs)
	resorts (and deletes) coefficients so that afterwards it has n_elements and the new coeff(i) has the previous value of coeff(map_to_old_coeff(i))

virtual void	set_primal (PrimalData *)
	if the minorant is generated by PrimalData and this should be aggregated along, insert a heap object of it here (see PrimalData)

virtual PrimalData *	get_primal ()
	returns NULL if there is no primal data and otherwise a pointer to it

virtual const PrimalData *	get_primal () const
	returns NULL if there is no primal data and otherwise a pointer to it (const version)

virtual Minorant *	clone_minorant (double factor=1., bool with_primal=true) const
	generates a full copy (multiplied by factor) on the heap and returns a pointer to it (it also includes a clone of the primal data if with_primal==true, otherwise the copy will have no primal data)

virtual int	aggregate (const Minorant &minorant, double factor=1.)
	adds factor*minorant to this and does this also for the primal if it is availabe

virtual int	number_aggregated () const
	returns the number of minorants aggregated in this one, value 1 thus means not aggregated

virtual int	scale_minorant (double scale_val)
	mutliply offset and coefficients (and PrimalData, if given) by scale_val

virtual double	norm_squared () const
	return the squared Euclidean norm

Protected Member Functions
	Minorant (const Minorant &)
	forbidden, blocked deliberately

Minorant &	operator= (const Minorant &)
	forbidden, blocked deliberately

Protected Attributes
MinorantData *	data
	implementation details are hidden on purpose

Detailed Description

this is used to describe affine minorants of convex functions that will be used for generating cutting models of these functions.

They have to be returned in calls to evaluation oracles like in FunctionOracle::evaluate() or MatrixFunctionOracle::evaluate().

The Minorant is of the form f(point)=offset+ inner_product(coeff,point), offset and coeff must be specified by the user by using the constructors or add_offset() and add_coeffs(). The dimension need not be specified (it is clear from point) and it is always assumed without actual checking that all nonzero coefficients are restricted to the dimension.

Sometimes it is more natural for the user to specify the offset at the point where the evaluation took place, in this case the minorant would have the form f(point)=offset+ inner_prodcut(coeff,point-evalpoint). If the user wants to avoid computing the offset with respect to the origin, it suffices to set offset_at_origin=false at initialization berfore returning the minorant.

Once a minorant is returned in an oracle evaluation, control over this object is handed over to ConicBundle. ConicBundle may want to and is allowed to clone or modify the minorants and will eventually delete this object. Thus a minorant (and all its associated date) must be an object on the heap.

The implementation of this class is given in Minorant.cxx

Constructor & Destructor Documentation

◆ Minorant() [1/3]

ConicBundle::Minorant::Minorant	(	double	offset,
		const DVector &	subg,
		PrimalData *	primal = `0`,
		bool	offset_at_origin = `false`
	)

Minorant constructor for a dense subgradient specified via a DVector.

Suppose in the evaluation of your oracle at the current point 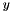$y$ you determine a subgradient 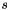$s$ for the subgradient inequality

$f(z)\ge f(y)+\langle s,z-y\rangle\quad\forall z\in\mathbf{R}^m,$

then use 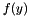$f(y)$ for offset and 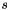$s$ in the form of a DVector in subg and keep the default value offset_at_origin == false.

If, on the other hand, your oracle implements a support function for some compact set 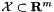$\mathcal{X}\subset\mathbf{R}^m$ like

$f(y) = \max_{x\in\mathcal{X}} x^\top y$

then it is actually more efficient to return 0 for offset, a maximizing 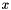$x$ in @ subg and to put offset_at_origin = true.

You may also pass over a PrimalData object in primal that will be then be owned and later deleted by the minorant and aggregated along with the minornat

◆ Minorant() [2/3]

ConicBundle::Minorant::Minorant	(	double	offset,
		const DVector &	subg_val,
		const IVector &	subg_ind,
		PrimalData *	primal = `0`,
		bool	offset_at_origin = `false`
	)

Minorant constructor for a sparse subgradient where the nonzero values are specified by DVector and the corresponding indices by an IVector.

Suppose in the evaluation of your oracle at the current point 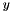$y$ you determine a subgradient 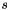$s$ with few nonzeros for the subgradient inequality

$f(z)\ge f(y)+\langle s,z-y\rangle\quad\forall z\in\mathbf{R}^m,$

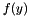then use $f(y)$ for offset and pass 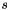$s$ by giving the nonzeros in the DVector subg_val, the corresponding indices in a IVector of the same length in subg_ind and keep the default value offset_at_origin == false.

If, on the other hand, your oracle implements a support function for some compact set 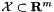$\mathcal{X}\subset\mathbf{R}^m$ like

$f(y) = \max_{x\in\mathcal{X}} x^\top y$

then it is actually more efficient to return 0 for offset, a sparse maximizing 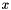$x$ in subg_val and subg_ind and to put offset_at_origin = true.

You may also pass over a PrimalData object in primal that will be then be owned and later deleted by the minorant and aggregated along with the minornat

◆ Minorant() [3/3]

ConicBundle::Minorant::Minorant	(	bool	offset_at_origin = `true`,
		double	offset = `0.`,
		int	n_elementes = `0`,
		const double *	coeffs = `0`,
		const int *	indices = `0`,
		double	scale_val = `1.`,
		PrimalData *	primal = `0`
	)

default initializes a zero minorant, see full explanation otherwise; NOTE: if the offset supplied by the minorant refers to the evaluation point (i.e., if it is the function value at the point of evaluation), set offset_at_origin = false !

In many applications, in particular for Lagrangian relaxation, the offset is more naturally given for the origin, and giving it this way also reduces computational cost a bit, so offset_at_origin = true is the suggested default. If, however, the minorant arises from a subgradient inequality by evaluation in the current point, you may as well give the function value as offset directly and set offset_at_origin=false;

The data specifying the minorant may be set here or (part of) it may be entered/added later. The meaning of the other parameters is as follows.

offset gives the constant value (if offset_at_origin = false then relative to the evaluation point)

n_elements gives the number of elements specified by coeffs (and possibly indices), but if coeffs == NULL it just asks to reserve space for that many coefficients

If coeffs is not NULL, it points to an array of doubles of size at least n_elements. If indices == NULL then coeff[i] belongs to position i for i=0 to n_elements-1, otherwise coeff[i] belongs to position indices[i]. All data is copied, the arrays are not modified, not used later and not deleted here.

The entire input data (offset and coefficients) is multplied by scale_val to give the final minorant (scale_val is not memorized internally but executed immediately).

If the minorant arises from PrimalData and the primal data should be aggregated along, it may be entered here or in the routine Minorant::set_primal(). The object pointed to is then owned by Minorant and will be deleted by Minorant on its destruction.

Member Function Documentation

◆ get_coeffs()

virtual int ConicBundle::Minorant::get_coeffs	(	int &	n_elements,
		const double *&	coeffs,
		const int *&	indices
	)		const

virtual

returns the list of all nonzero coefficients by returning pointers to the arrays and their common length n_elements

If on return coeffs==NULL this is interpreted as the zero vector. If on return indices==NULL, the indices are 0 to n_elements-1. If on return indices!=NULL, the entries of this array will be sorted in strictly increasing order

◆ get_dense_coeff_store()

virtual double* ConicBundle::Minorant::get_dense_coeff_store ( int n_elements )

virtual

If the returned pointer is not NULL it gives direct access to the array of current coefficient values with indices 0 up to n_elements-1;.

If the return value is NULL, the representation may not be available or access to the store may not be granted; in this case other routines like get_coeffs and add_coeffs have to be used.

This routine is mainly intended for increasing efficiency in some internal computations; the validity of the pointer returned may get lost with any call to any other routine of this Minorant, so during manipulations of the stored values no other routines should be called. Needless to say, this routine should only be used by experts.

The documentation for this class was generated from the following file:

CBSolver.hxx

Public Member Functions

Protected Member Functions

Protected Attributes