abstract interface that allows to use different 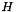 -norms
-norms 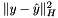 with a positive definite matrix
with a positive definite matrix 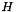 in the proximal term of the augmented model of ConicBundle::BundleSolver.
More...
in the proximal term of the augmented model of ConicBundle::BundleSolver.
More...
#include <BundleProxObject.hxx>

Public Member Functions | |
| BundleProxObject (VariableMetricSelection *vp=0, bool local_scaling=false, bool bounds_scaling=false, CBout *cb=0, int cbincr=-1) | |
| default constructor, switching on dynamic scaling only works for classes with corresponding support | |
| virtual void | set_weightu (CH_Matrix_Classes::Real weightu)=0 |
| in future computations the following weight must be included in the quadratic term (replacing the previous one) | |
| virtual void | set_short_QPsteps (CH_Matrix_Classes::Integer shortQPst) |
| may be used to indicate seemingly conservative step sizes possibly due to the quadratic term | |
| virtual CH_Matrix_Classes::Integer | get_short_QPsteps () |
| retrieves the number of conservative step sizes possibly due to the quadratic term passed on to this | |
| int | apply_factor (CH_Matrix_Classes::Real f) |
| allows AFTModel and SumModel to accumulate a compensation factor for tracing the effects of recursive applications of function_factor in update_model (does not affect H but can be retrieved by get_factor() for this purpose) | |
| CH_Matrix_Classes::Real | get_factor () |
| returns the current accumulated compensation factor by which H would need to be scaled in order to reflect the curvature relative to the current function without function_factor; | |
| virtual CH_Matrix_Classes::Real | get_weightu () const =0 |
| return the current weight incorporated in the quadratic term | |
| virtual CH_Matrix_Classes::Real | get_term_corr (void) const |
| return a correction factor for termination precision if the quadratic term is strong | |
| virtual CH_Matrix_Classes::Real | norm_sqr (const CH_Matrix_Classes::Matrix &B) const =0 |
return 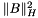 | |
| virtual CH_Matrix_Classes::Real | dnorm_sqr (const MinorantPointer &B) const =0 |
return 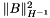 | |
| virtual bool | is_DLR () const =0 |
| return true if H is of the form diagonal matrix plus Gram matrix of a low rank matrix | |
| virtual int | add_H (CH_Matrix_Classes::Symmatrix &big_sym, CH_Matrix_Classes::Integer start_index=0) const =0 |
| add H to the dense symmetric matrix as a principal submatrix starting at position start_index | |
| virtual CH_Matrix_Classes::Matrix & | add_Hx (const CH_Matrix_Classes::Matrix &x, CH_Matrix_Classes::Matrix &outplusHx, CH_Matrix_Classes::Real alpha=1.) const =0 |
add 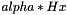 to outplusHx and return this to outplusHx and return this | |
| virtual CH_Matrix_Classes::Matrix & | apply_Hinv (CH_Matrix_Classes::Matrix &x) const =0 |
returns 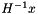 , possibly transformed by some AffineFunctionTransformation More... , possibly transformed by some AffineFunctionTransformation More... | |
| virtual void | get_precond (CH_Matrix_Classes::Matrix &D, const CH_Matrix_Classes::Matrix *&Vp) const =0 |
return 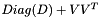 which either equals $H$ exactly (iff is_DLR() returns true) or, if not, serves as an approximation hopefully suitable for preconditioning. If $V$ is available it may be large, so return only a pointer to avoid copying. If no $V$ is available, then put Vp==0 on exit. which either equals $H$ exactly (iff is_DLR() returns true) or, if not, serves as an approximation hopefully suitable for preconditioning. If $V$ is available it may be large, so return only a pointer to avoid copying. If no $V$ is available, then put Vp==0 on exit. | |
| virtual int | compute_QP_costs (CH_Matrix_Classes::Symmatrix &Q, CH_Matrix_Classes::Matrix &d, CH_Matrix_Classes::Real &offset, const MinorantPointer &constant_minorant, const MinorantBundle &bundle, const CH_Matrix_Classes::Matrix ¢er_y, const MinorantPointer &groundset_minorant, CH_Matrix_Classes::Indexmatrix *yfixed)=0 |
| Compute the dual QP costs Q, d, and the constant offset to the bundle subproblem. More... | |
| virtual int | update_QP_costs (CH_Matrix_Classes::Symmatrix &delta_Q, CH_Matrix_Classes::Matrix &delta_d, CH_Matrix_Classes::Real &delta_offset, const MinorantPointer &constant_minorant, const MinorantBundle &bundle, const CH_Matrix_Classes::Matrix ¢er_y, const MinorantPointer &groundset_minorant, const MinorantPointer &delta_groundset_minorant, const CH_Matrix_Classes::Indexmatrix &delta_index, CH_Matrix_Classes::Indexmatrix *yfixed)=0 |
computes the update of the dual QP cost terms d and offset returned by compute_QP_costs() for changes in the ground set aggregate 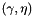 and in yfixed. More... and in yfixed. More... | |
| virtual int | apply_modification (const GroundsetModification &gsmdf)=0 |
| if the BundleSolver is called to modify the groundset it also calls this More... | |
| virtual BundleProxObject * | projected_clone (const CH_Matrix_Classes::Indexmatrix &indices)=0 |
| in order to allow for fixed variables, this generates a clone restricted to the given indices | |
 Public Member Functions inherited from ConicBundle::VariableMetric Public Member Functions inherited from ConicBundle::VariableMetric | |
| virtual | ~VariableMetric () |
| virtual destructor | |
| VariableMetric (VariableMetricSelection *vp=0, bool use_loc_metric=false, bool use_bnds_scaling=false, CBout *cbo=0, int cbinc=-1) | |
| default constructor; if vp is not zero, ownership of *vp is passed over to *this and *this will delete vp | |
| VariableMetricSelection * | get_variable_metric_selection () const |
| returns 0 or an available VariableMetricSelection object, that may be employed for computing a variable metric term in accordance with the value of use_local_metric | |
| void | set_variable_metric_selection (VariableMetricSelection *vp=0) |
| sets use_variable_metric; the object passed is then owned by this | |
| virtual bool | supports_dense_variable_metric () const |
| returns true if add_dense_variable_metric() is supported | |
| virtual bool | supports_lowrank_variable_metric () const |
| returns true if add_variable_metric() does not ignore the low rank argument vecH | |
| virtual bool | supports_diagonal_variable_metric () const |
| returns true if add_variable_metric() does not ignore the diagonal argument diagH | |
| bool | employ_variable_metric () const |
| returns true if some dynamic scaling is supported and switched on | |
| virtual int | apply_variable_metric (VariableMetricModel *, VariableMetricModel *, const CH_Matrix_Classes::Matrix &, CH_Matrix_Classes::Integer, const CH_Matrix_Classes::Matrix &, bool, CH_Matrix_Classes::Real &, CH_Matrix_Classes::Real, const CH_Matrix_Classes::Indexmatrix *=0) |
| the BundleSolver starts an update of this by dynamic scaling by calling this in every step; negative parameters give no preferences, but the global aggregate (groundset+model) has to be provided and if descent_step==false the scaling may only increase | |
| virtual int | add_variable_metric (CH_Matrix_Classes::Symmatrix &) |
| adds a suitable modification of symH (symH may be modified in this) to the scaling matrix H More... | |
| virtual int | add_variable_metric (CH_Matrix_Classes::Matrix &, CH_Matrix_Classes::Matrix &) |
| adds (a suitable modification of) Diag(diagH)+vecH*transpose(vecH) to the scaling matrix H (either matrix may be modified in this) More... | |
| virtual int | push_aft (const AffineFunctionTransformation *) |
| this AffineFunctionTransformation has to be used before applying Hinv in | |
| virtual int | pop_aft () |
| removes the top most aft (without deleting it!) | |
| bool | get_use_bounds_scaling () const |
| returns use_bounds_scaling | |
| void | set_use_bounds_scaling (bool bounds_scaling) |
| sets use_bounds_scaling | |
| virtual bool | supports_diagonal_bounds_scaling () const |
| if the respective implementation supports a diagonal bounds scaling heuristic, the following routine has to return true; see also diagonal_scaling_heuristic_update() | |
| bool | employ_diagonal_bounds_scaling () const |
| if the respective implementation supports a diagonal bounds scaling heuristic, the following routine has to return true; see also diagonal_bounds_scaling_update() | |
| virtual int | diagonal_bounds_scaling_update (const CH_Matrix_Classes::Matrix &) |
| if supported, D_update has to contain nonnegative numbers that are permanently added to the diagonal here. More... | |
| bool | get_use_local_metric () const |
| returns use_local_metric | |
| void | set_use_local_metric (bool local_metric) |
| sets use_local_metric | |
 Public Member Functions inherited from ConicBundle::CBout Public Member Functions inherited from ConicBundle::CBout | |
| virtual void | set_out (std::ostream *out=0, int print_level=1) |
| Specifies the output level (out==NULL: no output at all, out!=NULL and level=0: errors and warnings, level>0 increasingly detailed information) More... | |
| virtual void | set_cbout (const CBout *cb, int incr=-1) |
| Specifies the output level relative to the given CBout class. More... | |
| void | clear_cbout () |
| reset to default settings (out=0,print_level=1) | |
| CBout (const CBout *cb=0, int incr=-1) | |
| calls set_cbout | |
| CBout (std::ostream *outp, int pl=1) | |
| initialize correspondingly | |
| CBout (const CBout &cb, int incr=0) | |
| copy constructor | |
| virtual bool | cb_out (int pl=-1) const |
| Returns true if out!=0 and (pl<print_level), pl<0 should be used for WARNINGS and ERRORS only, pl==0 for usual output. | |
| std::ostream & | get_out () const |
| If cb_out() returned true, this returns the output stream, but it will abort if called with out==0. | |
| std::ostream * | get_out_ptr () const |
| returns the pointer to the output stream | |
| int | get_print_level () const |
| returns the print_level | |
| virtual int | mfile_data (std::ostream &out) const |
| writes problem data to the given outstream | |
 Public Member Functions inherited from ConicBundle::QPSolverProxObject Public Member Functions inherited from ConicBundle::QPSolverProxObject | |
| virtual | ~QPSolverProxObject () |
| virtual destructor | |
Protected Attributes | |
| CH_Matrix_Classes::Real | factor |
| used to accumulate a compensation factor for function_factor; this factor is not included in H but can be applied externally via get_factor() if required | |
| CH_Matrix_Classes::Integer | short_QPsteps |
| the QP may signal short steps that seem due to the quadratic term by setting this counter via set_short_QPsteps() | |
Static Protected Attributes | |
| static const CH_Matrix_Classes::Integer | xdim_threshold = 100 |
| constant for possible use if QP coefficients are to be computed in parallel (still purely experimental) | |
Detailed Description
abstract interface that allows to use different 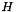 -norms
-norms 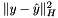 with a positive definite matrix
with a positive definite matrix 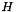 in the proximal term of the augmented model of ConicBundle::BundleSolver.
in the proximal term of the augmented model of ConicBundle::BundleSolver.
ConicBundle::BundleIdProx is the identitiy 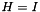 . There are further variants for diagonal scaling, low rank scaling or full scaling by a positive definite matrix.
. There are further variants for diagonal scaling, low rank scaling or full scaling by a positive definite matrix.
Member Function Documentation
◆ apply_Hinv()
|
pure virtual |
returns 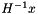 , possibly transformed by some AffineFunctionTransformation
, possibly transformed by some AffineFunctionTransformation
If a stack of instances of AffineFunctionTransformation has been added by push_aft() and A_1 to A_k are on the stack with A_k on top, then it returns 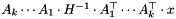
Implements ConicBundle::QPSolverProxObject.
Implemented in ConicBundle::BundleDiagonalTrustRegionProx, ConicBundle::BundleLowRankTrustRegionProx, ConicBundle::BundleDenseTrustRegionProx, ConicBundle::BundleDLRTrustRegionProx, and ConicBundle::BundleIdProx.
Referenced by get_term_corr().
◆ apply_modification()
|
pure virtual |
if the BundleSolver is called to modify the groundset it also calls this
The task is then to update the diagonal scaling information appropriately so that dimensions match and the proximal term makes sense for the modified problem.
Implemented in ConicBundle::BundleDiagonalTrustRegionProx, ConicBundle::BundleLowRankTrustRegionProx, ConicBundle::BundleDenseTrustRegionProx, ConicBundle::BundleDLRTrustRegionProx, and ConicBundle::BundleIdProx.
Referenced by get_term_corr().
◆ compute_QP_costs()
|
pure virtual |
Compute the dual QP costs Q, d, and the constant offset to the bundle subproblem.
Let 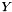 denote the (convex) feasible ConicBundle::Groundset and
denote the (convex) feasible ConicBundle::Groundset and 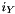 its indicator function, let
its indicator function, let 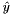 be the center of stability given by center_y, let
be the center of stability given by center_y, let 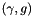 be the aggregate ground set minorant
be the aggregate ground set minorant 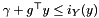 described by gs_subg_offset and gs_subg, let
described by gs_subg_offset and gs_subg, let 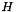 denote the positive definite scaling matrix with weight
denote the positive definite scaling matrix with weight 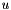 given by this class, and let
given by this class, and let 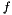 denote the objective for which ConicBundle::BundleModel holds the model
denote the objective for which ConicBundle::BundleModel holds the model 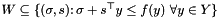 , which is assumed to be described in the form
, which is assumed to be described in the form 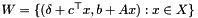 for some compact convex set
for some compact convex set 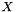 of dimension xdim. The routine computes the cost coefficients for the convex quadratic problem over
of dimension xdim. The routine computes the cost coefficients for the convex quadratic problem over 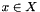 corresponding to the saddle problem
corresponding to the saddle problem
![\[ \max_{x\in X}\min_{y\in\mathbf{R}^n} [(b+Ax+g)^\top y + \gamma+\delta+c^\top x +\frac{u}2\|y-\hat y\|_H^2],\]](form_184.png)
This is indeed a convex QP in x because for each x the inner minimization over y is unconstrained and can be solved explicitly. So this gives rise to a problem
![\[ \max_{x\in X} -\frac12 x^\top Qx+d^\top x+\rho\]](form_185.png)
How to compute the cost coefficients 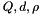 efficiently depends on the structural properties of
efficiently depends on the structural properties of 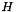 and therefore the costs are computed in this class.
and therefore the costs are computed in this class.
The data ![$[\delta,b]$](form_187.png) is provided by the offset constant minorant (its offset is
is provided by the offset constant minorant (its offset is 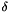 , its linear part
, its linear part 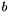 ), likewise the columns of
), likewise the columns of ![$[c^T;A]$](form_189.png) are provided by the xdim minorants of the bundle and
are provided by the xdim minorants of the bundle and 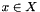 describes the admissible convex combinations which are not needed here.
describes the admissible convex combinations which are not needed here. 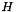 and
and 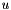 are the quadratic term and the weight, the latter is set in set_weightu(). The cost coefficients are
are the quadratic term and the weight, the latter is set in set_weightu(). The cost coefficients are 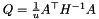 , d=...
, d=...
If some of the design variables are at their bounds and likely to only move out of bounds next they might be required to stay fixed by the calling routine and thus may not contribute to the cost coefficients of the dual QP other than by their contribution to the constant offset. These variables are indicated by a positive (nonzero) value in yfixed.
- Parameters
-
[out] Q (CH_Matrix_Classes::Symmatrix&) the quadratic cost term to be computed by this routine [out] d (CH_Matrix_Classes::Matrix&) the linear cost term to be computed by this routine [out] offset (CH_Matrix_Classes::Real&) the constant cost offset term to be computed by this routine [in] constant_minorant (const MinorantPointer&) together with the groundset_minorant its offset will yield 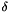 , and its linear part
, and its linear part 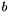 ),
),[in] bundle (const MinorantBundle&) their offsets form 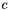 , their linear parts the columns of
, their linear parts the columns of 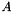 .
.[in] center_y (const CH_Matrix_Classes::Matrix&) the current center of stability of the bundle method, it is needed for computing linear cost term and constant coefficient [in] groundset_minorant (const MinorantPointer&) this is the aggregate subgradient 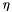 of the ground set it acts like a shift of the vector b forming the linear cost term for the y variables.
of the ground set it acts like a shift of the vector b forming the linear cost term for the y variables.[in,out] yfixed (CH_Matrix_Classes::Indexmatrix*) - if not NULL, on input the values of yfixed[i] are
- 0 if y_i us to be treated as a normal/non-fixed variable
- 1 if y_i is to be treated as a fixed value again
- 2 if y_i is newly fixed for the first time
- on output the last group, those with value 2 have to be set to 1 so that only values 0 and 1 remain
- if not NULL, on input the values of yfixed[i] are
- Returns
- 0 on success
- 1 on failure
Implemented in ConicBundle::BundleDiagonalTrustRegionProx, ConicBundle::BundleLowRankTrustRegionProx, ConicBundle::BundleDenseTrustRegionProx, ConicBundle::BundleDLRTrustRegionProx, and ConicBundle::BundleIdProx.
Referenced by get_term_corr().
◆ update_QP_costs()
|
pure virtual |
computes the update of the dual QP cost terms d and offset returned by compute_QP_costs() for changes in the ground set aggregate 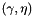 and in yfixed.
and in yfixed.
The update of the groundset aggregate 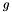 is given by delta_gs_subg and delta_index, more precisely, old_gs_subg[delta_index[i]]=gs_subg[delta_index[i]]-delta_gs_subg[i], where the current groundset aggregate gs_subg is the input paramter. delta_gs_subg_offset gives the change of
is given by delta_gs_subg and delta_index, more precisely, old_gs_subg[delta_index[i]]=gs_subg[delta_index[i]]-delta_gs_subg[i], where the current groundset aggregate gs_subg is the input paramter. delta_gs_subg_offset gives the change of 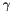 .
.
The entries of yfixed have the same meaning as in compute_QP_costs(): if yfixed[i]==0, variable y[i] is treated normally (not fixed); for yfixed[i]==1 the value was already considered fixed at center_y[i] in the computations before so it causes no changes at all; for yfixed[i]==2 the value is considered newly fixed at center_y[i], so its influence in the quadratic cost term Q and the linear term d have to be corrected (this case is the only reason for having delta_Q in the list of arguments). After this correction, put yfixed[i]=1 to signal that in the QP costs coordinate i is considered as fixed.
- Parameters
-
[out] delta_Q (CH_Matrix_Classes::Symmatrix&) the change in the quadratic cost term to be computed by this routine [out] delta_d (CH_Matrix_Classes::Matrix&) the change in linear cost term to be computed by this routine [out] delta_offset (CH_Matrix_Classes::Real&) the change in the constant cost offset term to be computed by this routine [in] constant_minorant (const MinorantPointer&) must be identical to the one used in compute_QP_costs [in] bundle (const CH_Matrix_Classes::Integer) must be identical to the one used in compute_QP_costs [in] center_y (const CH_Matrix_Classes::Matrix&) the current center of stability of the bundle method, [in] groundset_minorant (const MinorantPointer&) this is the aggregate subgradient 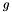 of the ground set
of the ground set[in] delta_groundset_minorant (const MinorantPointer&) this is the delta added to the previous value of the groundset aggregate to get the current aggregate subgradient 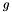 =groundset_minorant of the ground set
=groundset_minorant of the ground set[in] delta_index (const CH_Matrix_Classes::Indexmatrix&) holds the inidices where groundset_minorant or yfixed changed [in,out] yfixed (CH_Matrix_Classes::Indexmatrix*) - if not NULL, on input the values of yfixed[i] are
- 0 if y_i us to be treated as a normal/non-fixed variable
- 1 if y_i is to be treated as a fixed value again
- 2 if y_i is newly fixed for the first time
- on output the last group, those with value 2 have to be set to 1 so that only values 0 and 1 remain
- if not NULL, on input the values of yfixed[i] are
- Returns
- 0 on success
- 1 on failure
- See also
- compute_QP_costs
Implemented in ConicBundle::BundleDiagonalTrustRegionProx, ConicBundle::BundleLowRankTrustRegionProx, ConicBundle::BundleDenseTrustRegionProx, ConicBundle::BundleDLRTrustRegionProx, and ConicBundle::BundleIdProx.
Referenced by get_term_corr().
The documentation for this class was generated from the following file:
 1.8.13
1.8.13