abstract representation of the feasible convex ground set to be optimized over, provides the QP solver for the bundle subproblem as well as routines for computing feasible points and ground set aggregates More...

#include <Groundset.hxx>

Inheritance diagram for ConicBundle::Groundset:

Public Member Functions
virtual void	clear (CH_Matrix_Classes::Integer indim=0, CH_Matrix_Classes::Integer in_groundset_id=0)=0
	reset everything to initial state for an unconstrained ground set of dimension indim More...

virtual CH_Matrix_Classes::Integer	get_groundset_id () const =0
	returns the current groundset_id, increased values indicate changes in the ground set

virtual void	set_groundset_id (CH_Matrix_Classes::Integer gsid)=0
	sets the groundset_id to the desired value, increasing it is safer here because this is used to indicate changes

virtual CH_Matrix_Classes::Integer	get_dim () const =0
	returns the dimension of the ground set, i.e., the length of the variables vector y

virtual bool	constrained () const =0
	returns false if the feasible set is the entire space (unconstrained optimization), true otherwise. More...

virtual bool	is_feasible (CH_Matrix_Classes::Integer &in_groundset_id, const CH_Matrix_Classes::Matrix &y, CH_Matrix_Classes::Real relprec=1e-10)=0
	on input value in_groundset_id the input y was feasible. Return true if the id did not change, otherwise check if y is still feasible for the given precision. More...

virtual int	ensure_feasibility (CH_Matrix_Classes::Integer &in_groundset_id, CH_Matrix_Classes::Matrix &y, bool &ychanged, BundleProxObject *Hp=0, CH_Matrix_Classes::Real relprec=1e-10)=0
	if the groundset_id changed, it checks feasibility of y with respect to the given precision. If infeasible it replaces y by its projection with respect to the norm of Hp and sets ychanged to true. More...

virtual QPSolverObject *	get_qp_solver (bool &solves_model_without_gs, BundleProxObject *Hp)=0
	returns a pointer to an internal QPSolverObject that is able to solve bundle suproblems efficiently for this kind of groundset and scaling; if solves_model_without_gs == true the qp solver does not include the groundset and the groundset has to be dealt with by the Gauss Seidel approach

virtual int	set_qp_solver_parameters (QPSolverParametersObject *in_qpsp)=0
	set parameters for the QP_Solver

virtual const CH_Matrix_Classes::Matrix &	get_starting_point () const =0
	returns a stored starting point, note: this need not be feasible; if generated automatically, its dimension is correct.

virtual int	set_starting_point (const CH_Matrix_Classes::Matrix &vec)=0
	stores the a new starting point irrespective of whether it is feasible or not and returns 0 if it feasible, 1 if it is infeasible

virtual int	candidate (CH_Matrix_Classes::Integer &gs_id, CH_Matrix_Classes::Matrix &newy, CH_Matrix_Classes::Real &cand_gs_val, CH_Matrix_Classes::Real &linval, CH_Matrix_Classes::Real &augval_lb, CH_Matrix_Classes::Real &augval_ub, CH_Matrix_Classes::Real &subgnorm2, const CH_Matrix_Classes::Matrix &center_y, CH_Matrix_Classes::Real center_value, const MinorantPointer &model_minorant, BundleProxObject Hp, MinorantPointer delta_groundset_minorant=0, CH_Matrix_Classes::Indexmatrix *delta_index=0, CH_Matrix_Classes::Real relprec=1e-2)=0
	for a given model aggregate compute the groundset aggregate and the resulting (feasible) candidate More...

virtual const MinorantPointer &	get_gs_aggregate () const =0
	returns the groundset aggregate computed in candidate()

virtual const MinorantPointer &	get_gs_minorant () const =0
	returns the linear minorant valid on the entire ground set (e.g. a linear cost funciton)

virtual const CH_Matrix_Classes::Indexmatrix *	get_yfixed () const =0
	if not NULL (iff get_use_yfixing()==false) it returns the vector yfixed with yfixed(i)=0 if not fixed, =1 is fixed already, =2 if newly fixed

virtual CH_Matrix_Classes::Indexmatrix *	set_yfixed ()=0
	if not NULL (iff get_use_yfixing()==false) returns the vector yfixed with yfixed(i)=0 if not fixed, =1 is fixed already, =2 if newly fixed

virtual bool	get_use_yfixing () const =0
	true if the cooridinate fixing heuristic is switched on (only constrained cases)

virtual void	set_use_yfixing (bool uyf)=0
	set to true to switch on the cooridinate fixing heuristic (only constrained cases)

virtual GroundsetModification *	start_modification ()=0
	return a new modification object on the heap that is initialized for modification of *this

virtual int	apply_modification (const GroundsetModification &mdf)=0
	change the groundset description as specified by the argument

virtual int	mfile_data (std::ostream &out) const =0
	m-file output routine for debugging or testing in Matlab (not yet working)

Public Member Functions inherited from ConicBundle::VariableMetricModel
	VariableMetricModel (CBout *cb=0, int cbincr=-1)
	constructor for passing on ouptut information

virtual	~VariableMetricModel ()
	virtual destructor

virtual int	add_variable_metric (VariableMetric &H, CH_Matrix_Classes::Integer y_id, const CH_Matrix_Classes::Matrix &y, bool descent_step, CH_Matrix_Classes::Real weightu, CH_Matrix_Classes::Real model_maxviol, const CH_Matrix_Classes::Indexmatrix *indices=0)
	add to the variable metric information H some model dependent "second order" information of the function modelled More...

virtual VariableMetricModel *	variable_metric_transform ()
	Overload this in order apply transformations in between. More...

Public Member Functions inherited from ConicBundle::CBout
virtual void	set_out (std::ostream *out=0, int print_level=1)
	Specifies the output level (out==NULL: no output at all, out!=NULL and level=0: errors and warnings, level>0 increasingly detailed information) More...

virtual void	set_cbout (const CBout *cb, int incr=-1)
	Specifies the output level relative to the given CBout class. More...

void	clear_cbout ()
	reset to default settings (out=0,print_level=1)

	CBout (const CBout *cb=0, int incr=-1)
	calls set_cbout

	CBout (std::ostream *outp, int pl=1)
	initialize correspondingly

	CBout (const CBout &cb, int incr=0)
	copy constructor

virtual bool	cb_out (int pl=-1) const
	Returns true if out!=0 and (pl<print_level), pl<0 should be used for WARNINGS and ERRORS only, pl==0 for usual output.

std::ostream &	get_out () const
	If cb_out() returned true, this returns the output stream, but it will abort if called with out==0.

std::ostream *	get_out_ptr () const
	returns the pointer to the output stream

int	get_print_level () const
	returns the print_level

Detailed Description

abstract representation of the feasible convex ground set to be optimized over, provides the QP solver for the bundle subproblem as well as routines for computing feasible points and ground set aggregates

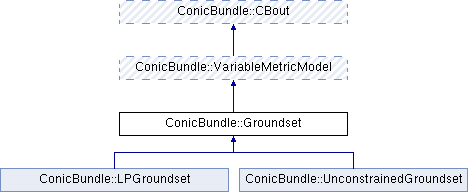
This class serves as abstract base class for all ground set classes.

Besides the main task of ensuring feasibility by producing a feasible starting point and by computing the ground set aggregate a lot of work is devoted to making problem changes efficient (addition/deletion of variables correspond to changes in dimension of the ground set) and to provide support for other dynamic decisions like fixing variables at their bounds if the bound appears to be strongly active.

A good way to think about the convex ground set is to imagine it to be given by the convex indicator function of the set. This indicator function is added to the cost function. The ground set aggregate is a linear minorant of the indicator function, usually it even corresponds to a subgradient inequality. E.g., if the ground set is the entire space, then zero is the only feasible groundset aggregate and the only useful offset is zero as well.

It is conceivable but currently not in use that the groundset also contributes to VariableMetric so as to support staying inside the feasible set. To allow for this in certain situations the Groundset is a derived class of a VariableMetricModel.

Member Function Documentation

◆ candidate()

virtual int ConicBundle::Groundset::candidate	(	CH_Matrix_Classes::Integer &	gs_id,
		CH_Matrix_Classes::Matrix &	newy,
		CH_Matrix_Classes::Real &	cand_gs_val,
		CH_Matrix_Classes::Real &	linval,
		CH_Matrix_Classes::Real &	augval_lb,
		CH_Matrix_Classes::Real &	augval_ub,
		CH_Matrix_Classes::Real &	subgnorm2,
		const CH_Matrix_Classes::Matrix &	center_y,
		CH_Matrix_Classes::Real	center_value,
		const MinorantPointer &	model_minorant,
		BundleProxObject *	Hp,
		MinorantPointer *	delta_groundset_minorant = `0`,
		CH_Matrix_Classes::Indexmatrix *	delta_index = `0`,
		CH_Matrix_Classes::Real	relprec = `1e-2`
	)

pure virtual

for a given model aggregate compute the groundset aggregate and the resulting (feasible) candidate

Let 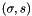$(\sigma,s)$ be the aggregate minorant 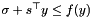$\sigma+s^\top y\le f(y)$ of the cost function described by model_subg_offset and model_subg, let 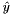$\hat y$ be the center of stability given by center_y, let 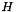$H$ denote the positive definite scaling matrix with weight 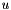$u$ given by Hp, let 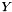$Y$ denote this (convex) feasible ground set and 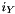$i_Y$ its indicator function, then this computes a saddle point 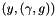$(y,(\gamma,g))$ of

$\max_{(\gamma,g)\in\partial i_Y}\min_{y\in\mathbf{R}^n} [(s+g)^\top y + \gamma+\sigma +\frac{u}2\|y-\hat y\|_H^2],$

The resulting 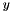$y$ is feasible and stored in newy. linval gets 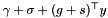$\gamma+\sigma+(g+s)^\top y$ , subgnorm2 gets 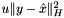$u\|y-\hat x\|_H^2$ , augval gets linval+subgnorm2 /2.

If delta_groundset_subg is not NULL, also elta_groundset_subg_offset and delta index are assumed to be not NULL. Then all changes from the previous groundset aggregate minorant to the new groundset aggregate minorant 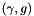$(\gamma,g)$ are stored in delta_groundset_subg_offset and delta_groundset_subg and delta_index holds the indices of the nonzero changes (mostly the groundset aggregate is sparse, e.g. due to complementarity). This is used in BundleProxObject::update_QP_costs().

On input 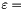$\varepsilon=$ relprec, 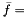$\bar f=$ center_value, and 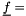$\underline{f}=$ augval serve to form appropriate stopping criteria if solving the saddle point problem requires a nonlinear convex optimization method. 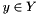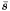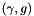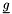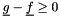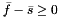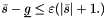The method is then assumed to produce a primal solution $y\in Y$ of value $\bar s$ and a dual solution $(\gamma,g)$ of value $\underline{g}$ with the properties $\underline g-\underline f\ge 0$ and $\bar f-\bar s\ge 0$ and $\bar s-\underline{g}\le\varepsilon(|\bar s|+1.)$ . In particular 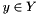$y\in Y$ is assumed to hold to machine precision.

If use_yfixing is true (the fixing heuristic is switched on), then 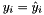$y_i=\hat y_i$ is required to hold for all i with yfixed(i)!=0, so these coordinates are not allowed to change. In particular, this routine may also set yfixed(i)=2 for new coordinates i, where 2 is used to indicate newly fixed variables. These will be reset to 1 in BundleProxObject::compute_QP_costs() and BundleProxObject::update_QP_costs() when this information has been digested.

In some derived classes a scaling heuristic is called that may influence the scaling Hp so as to avoid going outside the feasible region too far.

Parameters

[out]	gs_id	the current groundset_id
[out]	newy	the next candidate y (feasible)
[out]	cand_gs_val	the value of the groundset minorant in the candidate y (=groundset objective)
[out]	linval	(CH_Matrix_Classes::Real&) value of linear minorant in y
[in,out]	augval_lb	(CH_Matrix_Classes::Real&) on input: lower bound on value of augmented model in previous (maybe infeasible) candidate on output: lower bound on value of augmented model in y
[out]	augval_ub	(CH_Matrix_Classes::Real&) on output: upper bound on value of augmented model in y
[out]	subgnorm2	(CH_Matrix_Classes::Real&) squared Hp-norm (with weight) of joint groundset and model aggregate
[in]	center_y	(const CH_Matrix_Classes::Matrix&) center of stability (feasible)
[in]	center_value	(CH_Matrix_Classes::Real) function value in center_y
[in]	model_minorant	(const MinorantPoiner&) aggregate linear minorant of the cost function
[in,out]	Hp	(ConicBundle::BundleProxObject*) pointer to matrix H, may be influenced by a variable metric heuristic
[in,out]	delta_groundset_minorant	(MinorantPointer*) if not NULL, the change in groundset aggregate will be stored here
[in,out]	delta_index	(CH_Matrix_Classes::Indexmatrix*) must be not NULL iff delta_groundset_subg!=NULL or yfixed has changed, will store nonzero indices of delta_groundset_subg
[in]	relprec	(CH_Matrix_Classes::Real) relative precision for termination in QP computations

Returns: 0 on success, != 0 on failure

Implemented in ConicBundle::UnconstrainedGroundset, and ConicBundle::LPGroundset.

◆ clear()

virtual void ConicBundle::Groundset::clear	(	CH_Matrix_Classes::Integer	indim = `0`,
		CH_Matrix_Classes::Integer	in_groundset_id = `0`
	)

pure virtual

reset everything to initial state for an unconstrained ground set of dimension indim

Note that a ground set is allowed to have dimension zero. This will lead to evaluating a function without arguments and is a realistic scenario in Lagrangean relaxation of cutting plane approaches if no cutting planes have been added yet.

If the changes to the ground set are to be counted by groundset_id, then it makes sense to enter the appropriate value in in_groundset_id.

Implemented in ConicBundle::LPGroundset, and ConicBundle::UnconstrainedGroundset.

◆ constrained()

virtual bool ConicBundle::Groundset::constrained ( ) const

pure virtual

returns false if the feasible set is the entire space (unconstrained optimization), true otherwise.

The current class implements the unconstrained case and always returns false.

Implemented in ConicBundle::LPGroundset, and ConicBundle::UnconstrainedGroundset.

◆ ensure_feasibility()

virtual int ConicBundle::Groundset::ensure_feasibility	(	CH_Matrix_Classes::Integer &	in_groundset_id,
		CH_Matrix_Classes::Matrix &	y,
		bool &	ychanged,
		BundleProxObject *	Hp = `0`,
		CH_Matrix_Classes::Real	relprec = `1e-10`
	)

pure virtual

if the groundset_id changed, it checks feasibility of y with respect to the given precision. If infeasible it replaces y by its projection with respect to the norm of Hp and sets ychanged to true.

The routine is called by the internal bundle solver to check whether the given center is still valid (in some applications the groundset might change during the runtime of the bundle method), where, if ychanged is false on input, validity of y was already checked at a point in time when the groundset had the in_groundset_id. If ychanged==false and the groundset_id is still the same, then y is simply assumed to be still correct (the precision is not even looked at in this case). Otherwise the routine checks the validitiy of y with respect to the given precision. If feasible, it returns the new groundset_id in in_groundset_id and keeps ychanged unaltered. If y is infeasible, the rountine computes its projection onto the feasible set with respect to the norm of Hp (if ==0 then the Euclidean norm is used), stores it in y, sets ychanged to true, sets in_groundset_id to the current groundset_id and returns 0. Should anything go wrong, it returns 1.

This concrete base class represents the unconstrained case, so feasiblity only checks the dimension and never requires projections.

Implemented in ConicBundle::LPGroundset, and ConicBundle::UnconstrainedGroundset.

◆ is_feasible()

virtual bool ConicBundle::Groundset::is_feasible	(	CH_Matrix_Classes::Integer &	in_groundset_id,
		const CH_Matrix_Classes::Matrix &	y,
		CH_Matrix_Classes::Real	relprec = `1e-10`
	)

pure virtual

on input value in_groundset_id the input y was feasible. Return true if the id did not change, otherwise check if y is still feasible for the given precision.

The routine is called by the internal bundle solver to check whether the given center is still valid (in some applications the groundset might change during the runtime of the bundle method), where validity of y was already checked at a point in time when the groundset had the in_groundset_id. If the groundset_id is still the same, then y is simply assumed to be still correct (the precision is not even looked at in this case). Otherwise the routine checks the validitiy of y with respect to the given precision but does not enforce validity. It returns true if y is valid and false otherwise.

Implemented in ConicBundle::LPGroundset, and ConicBundle::UnconstrainedGroundset.

The documentation for this class was generated from the following file:

Groundset.hxx

Public Member Functions

Detailed Description

Member Function Documentation

◆ candidate()

◆ clear()

◆ constrained()

◆ ensure_feasibility()

◆ is_feasible()