Oracle interface for minimization of the support function over the seoncd order cone with 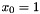$x_0=1$ for an affine cost function or, equivalently, Lagrangian relaxation of second order cone programs. More...

#include <SOCOracle.hxx>

Inheritance diagram for ConicBundle::SOCOracle:

Public Member Functions
virtual Minorant *	generate_minorant (const CH_Matrix_Classes::Matrix &SOCvec)=0
	generates the minorant that arises from the given second order cone vector. The minorant must allow some primal aggregation. More...

virtual int	extract_SOCvector (CH_Matrix_Classes::Matrix &SOCvec, const Minorant *SOCminorant)=0
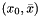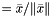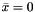	given a minorant arising from convex combinations of minorants produced by generate_minorant() it determines a $(x_0,\bar x)$ generating it and returns SOCvec $=\bar x/\\|\bar x\\|$ or some unit vector if $\bar x=0$ . More...

virtual int	projection (CH_Matrix_Classes::Matrix &offset, CH_Matrix_Classes::Matrix &coeffs, const CH_Matrix_Classes::Matrix &bar_P, const CH_Matrix_Classes::Indexmatrix *index_subset=0)=0
	compute projected coefficient matrices More...

virtual int	evaluate (const CH_Matrix_Classes::Matrix &current_point, const CH_Matrix_Classes::Real relprec, CH_Matrix_Classes::Real &SOC_value, CH_Matrix_Classes::Matrix &SOC_vector, SOCPrimalExtender *&primal_extender)=0

virtual int	evaluate_projection (const CH_Matrix_Classes::Matrix &current_point, const CH_Matrix_Classes::Matrix &P, const CH_Matrix_Classes::Real relprec, CH_Matrix_Classes::Real &projected_SOC_value)=0

virtual int	apply_modification (const OracleModification &, const CH_Matrix_Classes::Matrix , const CH_Matrix_Classes::Matrix , bool &, bool &, bool &, MinorantExtender *&)
	This routine need not be implemented unless variables (constraints in Lagrangean relaxation) are added or deleted on the fly. More...

virtual bool	check_correctness () const
	switch on/off some correctnes checks on the oracle

Public Member Functions inherited from ConicBundle::ModifiableOracleObject
virtual	~ModifiableOracleObject ()
	virtual destructor

Detailed Description

Oracle interface for minimization of the support function over the seoncd order cone with 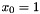$x_0=1$ for an affine cost function or, equivalently, Lagrangian relaxation of second order cone programs.

Within the setting explained in abstract second order cone oracle the abstract class SOCOracle defines a matrix free interface to the support function and the action of the affine cost function 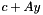$c+Ay$ for the second order bundle cutting model implemented in SOCModel. In particular, it provides in

generate_minorant() the minorant corresponding to a SOC element (with primal data for primal aggregation)
extract_SOCvector() returns for a minorant the SOC vector that gives rise to this minorant (for this all minorants must include this primal data)
projection() the projection of the affine cost function data onto a subspace of 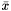$\bar x$ spanned by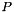
evaluate() for given 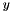the function value for the affine cost vector or a SOC vector with sufficiently high SOC_value to exceed the threshold for null steps in the bundle method
evaluate_projection() for given 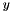the same as in evaluate but now for the projected affine matrix function where 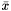$\bar x$ is restricted to the span of .
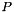and the function check_correctness() with the same meaning as in ConicBundle::FunctionOracle

For a concrete implementation of SOCOracle see ConicBundle::AffineMatrixFunction .

Member Function Documentation

◆ apply_modification()

virtual int ConicBundle::SOCOracle::apply_modification	(	const OracleModification &	,
		const CH_Matrix_Classes::Matrix *	,
		const CH_Matrix_Classes::Matrix *	,
		bool &	,
		bool &	,
		bool &	,
		MinorantExtender *&
	)

inlinevirtual

This routine need not be implemented unless variables (constraints in Lagrangean relaxation) are added or deleted on the fly.

The routine is only called by the solver if the variables indeed get modified by the solver or a modification is passed on by the user via the solver interface. oracle_modification is then used to either transfer user supplied instructions to the oracle on how to modify itself or to inform the oracle about changes the solver was asked to perform on the variables. If available, the solver will also show the effect of these changes on the center point in new_center and old_center; if these are not available then they hold NULL. A user supplied oracle_modification will be checked for consistency with the actual changes in the variables and mismatches will cause failures.

The remaining variables are output variables by which the oracle tells the solver which information has a chance to be preserved in view of these changes. If e.g. the deletion of some nonzero variables invalidates the function value in the new center, the oracle has to set discard_objective_in_center=true. If the entire model cannot be preserved (this includes the aggregates and the function values), the oracle needs to set discard_model=true; If only aggregate minorants cannot be preserved, the oracle needs to set discard_aggregates=true; in the current implementation of SOCModel this removes all minorants generated by generate_minorant() because each of them is typically generated by more than one Ritz vector. Whenever new variables were added, the model can only be preserved if the remaining minorants (maybe without aggregates) can be extended for these new variables. In this case the oracle has to supply the appropriate MinorantExtender via minorant_extender and only those minorants will be kept for which this operation succeeds.

Return value 0 indicates that these actions allow to continue without errors, other return values result in an overall error on these changes.

Reimplemented from ConicBundle::ModifiableOracleObject.

Reimplemented in ConicBundle::SOCSupportFunction.

◆ evaluate()

virtual int ConicBundle::SOCOracle::evaluate	(	const CH_Matrix_Classes::Matrix &	current_point,
		const CH_Matrix_Classes::Real	relprec,
		CH_Matrix_Classes::Real &	SOC_value,
		CH_Matrix_Classes::Matrix &	SOC_vector,
		SOCPrimalExtender *&	primal_extender
	)

pure virtual

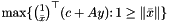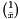computes $\max\{{1 \choose \bar x}^\top(c+Ay)\colon 1\ge\|\bar x\|\}$ and returns the value and a maximizing vector ${1 \choose \bar x}$ .

Returns: 0 on success

Parameters

current_point	argument = current variables = position where to evaluate the function
relprec	The columns of the matrix are orthonormal bundle vectors and may help to construct good startig vectors for the eigenvalue computation by iterative methods but have no other use. bundlevecs may have dimension 0.
SOC_value	on input: gives the threshold for a null step; a vector is good enough to yield sufficient improvement if its value exceeds this SOC_value.

on output: the value obtained for the returned SOC_vector; if it is smaller than the input SOC_value, then ist must be guaranteed to lie within relprec*(max(abs(SOC_value),1.)) of the true optimum

Parameters

	SOC_vector
[out]	SOC_vector	return a maximizing vector 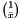${1\choose \bar x}$
	primal_extender
[out]	primal_extender	(PrimalExtender*&) if primal_data or vectors provided in (minonrants of) previous calls now have to be updated due to changes in the primal problem – e.g., this may happen in column generation – one may return a pointer to a SOCPrimalExtender object on the heap. This object will be used by ConicBundle to update all its internally stored vectors and primal_data objects in its minorants by calling PrimalExtender::extend on each of these. Afterwards ConicBundle deletes primal_extender. If this is not needed, set the variable to NULL.

Implemented in ConicBundle::SOCSupportFunction.

◆ evaluate_projection()

virtual int ConicBundle::SOCOracle::evaluate_projection	(	const CH_Matrix_Classes::Matrix &	current_point,
		const CH_Matrix_Classes::Matrix &	P,
		const CH_Matrix_Classes::Real	relprec,
		CH_Matrix_Classes::Real &	projected_SOC_value
	)

pure virtual

compute SOC maximum for the restricted 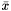$\bar x$ subspace spanned by P

Returns: 0 on success

Parameters

current_point	argument = current variable values = position where to evaluate the function
P	orthogonal matrix defining the projection;
relprec	relative precision requirement
projected_SOC_value	output: ortho

Implemented in ConicBundle::SOCSupportFunction.

◆ extract_SOCvector()

virtual int ConicBundle::SOCOracle::extract_SOCvector	(	CH_Matrix_Classes::Matrix &	SOCvec,
		const Minorant *	SOCminorant
	)

pure virtual

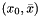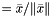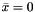given a minorant arising from convex combinations of minorants produced by generate_minorant() it determines a $(x_0,\bar x)$ generating it and returns SOCvec $=\bar x/\|\bar x\|$ or some unit vector if $\bar x=0$ .

This routine is needed when returning from a polyhedral model used by a SumBundleHandler in order to reconstruct an aggregate direction for the conic model. Note that generate_minorant has to provide suitable primal information for this, so that the convex combinations of the minorants allow this reconstruction.

Implemented in ConicBundle::SOCSupportFunction.

◆ generate_minorant()

virtual Minorant* ConicBundle::SOCOracle::generate_minorant ( const CH_Matrix_Classes::Matrix & SOCvec )

pure virtual

generates the minorant that arises from the given second order cone vector. The minorant must allow some primal aggregation.

The returned minorant must satisfy offset_gives_value_at_origin()==true. The minorant is passed over to the caller and will be deleted there. From a convex combination of such minorants the routine extract_SOCvec() must be able to reproduce a suitable SOCvec, see there.

Implemented in ConicBundle::SOCSupportFunction.

◆ projection()

virtual int ConicBundle::SOCOracle::projection	(	CH_Matrix_Classes::Matrix &	offset,
		CH_Matrix_Classes::Matrix &	coeffs,
		const CH_Matrix_Classes::Matrix &	bar_P,
		const CH_Matrix_Classes::Indexmatrix *	index_subset = `0`
	)

pure virtual

compute projected coefficient matrices

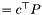The projection matrix is $P=\left[\begin{array}{cc}1 & 0 \\ 0 & \bar P \end{array}\right]$ . offset $=c^\top P$ always has to be computed. If index_subset==0, row i of coeffs is filled with row i of 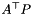$A^\top P$ for i=1,dots,m If index_subset!=0, row i of coeffs holds the row (*index_subset)(i)

Implemented in ConicBundle::SOCSupportFunction.

The documentation for this class was generated from the following file:

SOCOracle.hxx

Public Member Functions

Detailed Description

Member Function Documentation

◆ apply_modification()

◆ evaluate()

◆ evaluate_projection()

◆ extract_SOCvector()

◆ generate_minorant()

◆ projection()