for minimizing the support function over the second order cone with 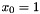$x_0=1$ for an affine cost function or, equivalently, Lagrangian relaxation of Linear Programs over the second order cone More...

Classes
class	ConicBundle::SOCPrimalExtender
	Interface for extending PrimalData, e.g., in Lagrangian relaxation of column generation approaches. More...

class	ConicBundle::SOCOracle
	Oracle interface for minimization of the support function over the seoncd order cone with 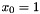for an affine cost function or, equivalently, Lagrangian relaxation of second order cone programs. More...

class	ConicBundle::SOCBundleParameters
	Bundle parameters for SOCModel. More...

Detailed Description

for minimizing the support function over the second order cone with 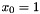$x_0=1$ for an affine cost function or, equivalently, Lagrangian relaxation of Linear Programs over the second order cone

For a vector 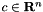$c\in\mathbf{R}^n$ and a matrix 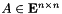$A\in\mathbf{E}^{n\times n}$ (explicitly or implicitly given), the abstract SOCOracle represents one of the following convex functions 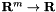$\mathbf{R}^m\to\mathbf{R}$ depending on the selected parameter ConicBundle::FunctionTask and the scalar factor 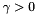$\gamma>0$ when adding the function to the problem by MatrixCBsolver::add_function(),

$f_\gamma(y)=\gamma \max\{{1 \choose \bar x}^\top(c+Ay)\colon 1\ge\|\bar x\|\}$

$f^+_\gamma(y)=\gamma \max\{0,{1 \choose \bar x}^\top(c+Ay)\colon 1\ge\|\bar x\|\}$

$f^+_\infty(y)=\gamma \max\{0,{1 \choose \bar x}^\top(c+Ay)\colon 1\ge\|\bar x\|\} \mbox{ with }\gamma\to \infty.$

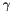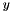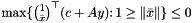While $\gamma$ is the fixed value given explicitly in MatrixCBsolver::add_function() in the first two cases, in the last case only the initial value is supplied and then solver and model successively determine new values so as to ensure (if feasible) that in the end solutions $y$ (almost) satisfy $\max\{{1 \choose \bar x}^\top(c+Ay)\colon 1\ge\|\bar x\|\}\le 0$ .

The solver exploits a SOCOracle by using a specialized SOCModel which implements a cutting model similar to the spectral bundle method, i.e., the cutting surface is determined by optimizing over a succsively updated subspace for 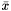$\bar x$ . The approach is explicitly intended for large scale applications, therefore SOCOracle never supplies the coefficient matrices explicitly but provides access to computing their action on given vectors or matrices and to the evaluation of the function for given 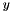$y$ . In this sense it is a matrix free oracle. For an implementation that supports sparse matrices see implemention of a SOCOracle (SOCSupportFunction). In special situations it may also be worth to implement a corresponding specialized class derived from SOCOracle.

If in setting up groundset within MatrixCBSolver the 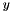$y$ variables are introduced with a linear cost vector 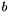$b$ and appropriate sign constraints, the three functions above may be interpreted as the Lagrangian dual to a primal semidefinite program of the form

$\mbox{maximize }c^\top x\rangle \mbox{ subject to } A^\top x\begin{array}{c}\le\\=\\\ge\end{array}b, x_0\begin{array}{c}\le\\=\end{array}\gamma, ~~ x_0\ge \|\bar x\| \mbox{ with }x={x_0\choose\bar x}$

The constraint on 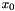$x_0$ is always added implicitly and its type is guided by the choice of ConicBundle::FunctionTask in MatrixCBSolver::add_function(). In particular

ObjectiveFunction represents the constraint 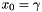$x_0=\gamma$ . Lagrangian relaxation of the constraints 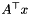$A^\top x$ by multipliers 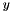then results in the dual function 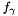$f_\gamma$ . Note, if the other constraints already imply 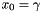$x_0 =\gamma$ , the dual solution 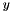will not be unique, because adding a constant to the first component of 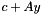will give rise to the same objective value.
ConstantPenaltyFunction represents the constraint 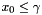$x_0\le\gamma$ . Lagrangian relaxation of the constraints 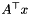$A^\top x$ by multipliers 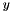results in the dual function 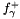$f_\gamma^+$ . It corresponds to a primal feasible set having $x_0$ bounded by 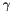$\gamma$ . If a bound on the size of the primal optimal solution is known in advance, this is a good choice for 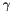$\gamma$ , and this variant is then more suitable than the next and last one.
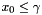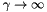AdaptivePenaltyFunction represents the constraint $x_0\le\gamma$ for $\gamma \to \infty$ , so in fact this only leads to 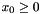$x_0\ge 0$ . Lagrangian relaxation of the constraints 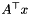$A^\top x$ by multipliers 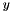results in the dual function 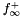$f_\infty^+$ . The given initial value of 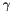$\gamma$ will be increased by SOCModel whenever there is no progress in forcing the support function value of the affine cost function to a value of at most 0. If the primal problem has a bounded optimal solution, this will end at some point, but 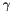$\gamma$ might get too large for keeping numerical stability. In general this option is still a bit hazardous, the other two variants are clearly to be preferred. In particular, if a good bound on reasonable sizes of optimal solutions are known, it is suggested to choose ConstantPenaltyFunction instead.

In terms of the primal SOC view the sense of the constraints 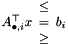$A_{\bullet,i}^\top x \begin{array}{c}\le\\=\\\ge\end{array} b_i$ is determined by the sign constraints on the dual variables 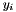$y_i$ and these must be encoded in the ConicBundle::Groundset of the y variables, these bounds and the right hand side are not provided by this oracle. The right hand side can be added e.g. as a linear cost term for the variables 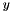$y$ or alternatively via an AffineFunctionTransformation.

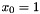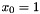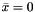The bundle method computes the cutting model by successively computing and collecting extreme rays of the second order cone with $x_0=1$ in addition to the unit vector having $x_0=1$ and $\bar x=0$ . The proper convex/conic combination of these (computed by the method) successively approximates an optimal solution 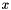$x$ to the primal SOC. As this primal approximation is often the central object of interest (e.g. it is the basis for cutting plane approaches) the method can be instructed to collect this primal information explicitly by supplying some MatrixPrimal in the implementation of SOCOracle::generate_minorant().

For a concrete implementation of SOCOracle using Matrix Classes (namespace CH_Matrix_Classes) see implemention of a SOCOracle (SOCSupportFunction).

Internally, the SumBlockModel implementation of the bundle model is SOCModel.