PSCAffineFunction is an implementation of ConicBundle::PSCOracle for the minimization of the maximum eigenvalue of an affine matrix function or, equivalently, Lagrangian relaxation of Linear Programs over the cone of positive semidefinite matrices. More...
Classes | |
| class | ConicBundle::PSCAffineMinorantExtender |
| Implementation of MinorantExtender for PSCAffineFunction. More... | |
| class | ConicBundle::PSCAffineFunction |
| general purpose implementation of PSCOracle as explained in implemention of a PSCOracle (PSCAffineFunction) More... | |
| class | ConicBundle::PSCPrimal |
| PSCPrimal is the corresponding positive semidefinite object for PSCOracle like PrimalMatrix for a MatrixFunctionOracle. More... | |
| class | ConicBundle::PSCAffineModification |
| class for collecting and organizing a sequence of changes to block diagonal symmetric affine matrix functions so that it can be carried out in one step later on; More... | |
| class | ConicBundle::CoeffmatInfo |
| allows to memorize the scalings applied to a Coeffmat and offers the basis for storing further user defined informations on a Coeffmat More... | |
| class | ConicBundle::CMIName |
| extends CoeffmatInfo to store a name (e.g. of the constraint it represents) More... | |
| class | ConicBundle::Coeffmat |
| defines a base class for coefficient matrices in semidefinite programming, in particular for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction). More... | |
| class | ConicBundle::CoeffmatPointer |
| pointer class for Coeffmat for deleting objects on the heap if Coefmat::use_cnt is reduced to zero and deletion is allowed. More... | |
| class | ConicBundle::CMsymdense |
| implements a general dense symmetric Coeffmat based on CH_Matrix_Classes::Symmatrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... | |
| class | ConicBundle::CMsymsparse |
| implements a general sparse symmetric Coeffmat based on CH_Matrix_Classes::Sparsesym (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... | |
| class | ConicBundle::CMgramdense |
implements a Gram matrix 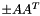 as Coeffmat for a dense rectangular CH_Matrix_Classes::Matrix as Coeffmat for a dense rectangular CH_Matrix_Classes::Matrix 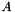 (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... | |
| class | ConicBundle::CMgramsparse |
implements a Gram matrix 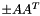 as Coeffmat for a sparse rectangular CH_Matrix_Classes::Sparsemat as Coeffmat for a sparse rectangular CH_Matrix_Classes::Sparsemat 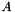 (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... | |
| class | ConicBundle::CMgramsparse_withoutdiag |
implements a Gram matrix 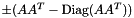 with zero diagonal as Coeffmat for a sparse rectangular CH_Matrix_Classes::Sparsemat with zero diagonal as Coeffmat for a sparse rectangular CH_Matrix_Classes::Sparsemat 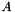 (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... | |
| class | ConicBundle::CMlowrankdd |
implements a low rank matrix 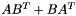 as Coeffmat with as Coeffmat with 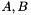 each a dense rectangular CH_Matrix_Classes::Matrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... each a dense rectangular CH_Matrix_Classes::Matrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... | |
| class | ConicBundle::CMlowranksd |
implements a low rank matrix 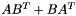 as Coeffmat with as Coeffmat with 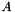 a sparse rectangular CH_Matrix_Classes::Sparsemat and a sparse rectangular CH_Matrix_Classes::Sparsemat and 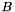 a dense rectangular CH_Matrix_Classes::Matrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... a dense rectangular CH_Matrix_Classes::Matrix (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... | |
| class | ConicBundle::CMlowrankss |
implements a low rank matrix 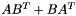 as Coeffmat with as Coeffmat with 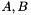 each a sparse rectangular CH_Matrix_Classes::Sparsemat (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... each a sparse rectangular CH_Matrix_Classes::Sparsemat (for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction)). More... | |
| class | ConicBundle::CMsingleton |
| implements a Coeffmat having just one nonzero element (or two by symmetry) for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction). More... | |
| class | ConicBundle::Bigmatrix |
AffineMatrixFunction needs to compute the maximum eigenvalue of an affine matrix function 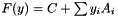 . This class prepares . This class prepares 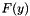 in useful form for iterative eigenvalue solvers. More... in useful form for iterative eigenvalue solvers. More... | |
Functions | |
| ConicBundle::PSCAffineMinorantExtender::PSCAffineMinorantExtender (PSCAffineFunction *amf) | |
| the PSCAffineFunction pointed to has to be valid for the livetime of this object | |
| int | ConicBundle::PSCAffineMinorantExtender::extend (Minorant &minorant, int n_coords, const int *indices) |
| called by ConicBundle to update internal Minorant objects, has to return 0 on success More... | |
| int | ConicBundle::PSCAffineFunction::form_bigmatrix (const CH_Matrix_Classes::Matrix ¤t_point) |
| compute the Bigmatrix representation for the given point | |
| int | ConicBundle::PSCAffineFunction::apply_modification (const PSCAffineModification &amfmod) |
| applies the PSCAffineModfication amfmod to the current function | |
| void | ConicBundle::PSCAffineFunction::clear () |
| resets all to the initial empty state | |
Initialization and setting parameters | |
| ConicBundle::PSCAffineFunction::PSCAffineFunction (const CBout *cb=0, int incr=-1) | |
| ConicBundle::PSCAffineFunction::PSCAffineFunction (const SparseCoeffmatMatrix &C, const SparseCoeffmatMatrix &opAt, PSCPrimal *generating_primal=0, const CBout *cb=0, int incr=-1) | |
| initialize the PSCAffineFunction with its matrices and possible a generating_primal More... | |
| ConicBundle::PSCAffineFunction::~PSCAffineFunction () | |
| void | ConicBundle::PSCAffineFunction::set_check_correctness (bool chk) |
| set the maximum number of Ritz vectors returned in evaluate(), see implemention of a PSCOracle (PSCAffineFunction) More... | |
| void | ConicBundle::PSCAffineFunction::set_max_Ritzvecs (CH_Matrix_Classes::Integer maxv) |
| set the maximum number of new Ritzvectors returned by evaluate(); values<1 default to 5 | |
routines for querying data of the problem | |
| const SparseCoeffmatMatrix & | ConicBundle::PSCAffineFunction::get_opAt () |
| const SparseCoeffmatMatrix & | ConicBundle::PSCAffineFunction::get_C () |
| const PSCPrimal * | ConicBundle::PSCAffineFunction::get_generating_primal (void) |
| returns the current setting concerning the generation of an PSCPrimal (0 for none) | |
routines for supporting input and output | |
| void | ConicBundle::PSCAffineFunction::set_out (std::ostream *o=0, int pril=1) |
| see ConicBundle::CBout | |
| void | ConicBundle::PSCAffineFunction::set_cbout (const CBout *cb, int incr=-1) |
| see ConicBundle::CBout | |
| std::ostream & | ConicBundle::PSCAffineFunction::print_problem_data (std::ostream &out) const |
| write the problem description to out so that it can be read again by read_problem_data() | |
| std::istream & | ConicBundle::PSCAffineFunction::read_problem_data (std::istream &in) |
| clear() and read the problem from in in the format written by print_problem_data() | |
| std::ostream & | ConicBundle::PSCAffineFunction::print_problem_data_to_mfile (std::ostream &out, CH_Matrix_Classes::Integer blocknr) const |
| undocumented highly volatile variant for external testing | |
| typedef std::vector< CoeffmatPointer > | ConicBundle::CoeffmatVector |
| convenient for initializing SparseCoeffmatMatrix via the sparse (block_i,column_i,Coeffmat_i), i=1,...,nz (nonzeros) format with Indexmatrix,Indexmatrix,CoeffmatVector | |
| typedef std::map< CH_Matrix_Classes::Integer, CoeffmatPointer > | ConicBundle::SparseCoeffmatVector |
| this is used to extract a row/block or a column from a SparseCoeffmatMatrix | |
| enum | ConicBundle::Coeffmattype { ConicBundle::CM_unspec =0, ConicBundle::CM_symdense =1, ConicBundle::CM_symsparse =2, ConicBundle::CM_lowrankdd =3, ConicBundle::CM_lowranksd =4, ConicBundle::CM_lowrankss =5, ConicBundle::CM_gramdense =6, ConicBundle::CM_gramsparse =7, ConicBundle::CM_singleton =8, ConicBundle::CM_gramsparsewd =9 } |
| for recognizing the type when writing and reading the problem More... | |
| CoeffmatInfo * | ConicBundle::clone (const CoeffmatInfo *cip) |
| if cip is not zero, it calls and returns cip->clone() and 0 otherwise | |
| Coeffmat * | ConicBundle::coeffmat_read (std::istream &in) |
| reads the next Coeffmat from in into an object on the heap and returns a pointer to it. The caller has to destruct the object. | |
Detailed Description
PSCAffineFunction is an implementation of ConicBundle::PSCOracle for the minimization of the maximum eigenvalue of an affine matrix function or, equivalently, Lagrangian relaxation of Linear Programs over the cone of positive semidefinite matrices.
The class PSCAffineFunction implements a general purpose version of PSCOracle for minimizing the ( 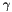 -weighted) maximum eigenvalue
-weighted) maximum eigenvalue 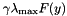 of an affine matrix function
of an affine matrix function 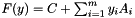 , see abstract positive semidefinite cone oracle for an explanation of the general setting and the connections to Lagrangian relaxation of SDPs of the form
, see abstract positive semidefinite cone oracle for an explanation of the general setting and the connections to Lagrangian relaxation of SDPs of the form
![\[ \mbox{maximize }\langle C,X\rangle \mbox{ subject to } \langle -A_i,X\rangle \begin{array}{c}\le\\=\\\ge\end{array} b_i,~~ \langle I,X\rangle \begin{array}{c}\le\\=\end{array}\gamma,~~ X\succeq 0 \]](form_333.png)
PSCAffineFunction supports a rich variety of special choices for the matrices 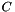 and
and 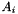 and uses (for large matrices) an iterative Lanczos method to compute eigenvalues and eigenvectors of
and uses (for large matrices) an iterative Lanczos method to compute eigenvalues and eigenvectors of 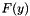 . In particular, the matrices
. In particular, the matrices 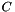 and
and 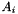 may consist of a single or several diagonal blocks (the dimensions of the blocks have to be consistent for
may consist of a single or several diagonal blocks (the dimensions of the blocks have to be consistent for 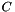 and the
and the 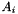 ), each block being a coefficient matrix of the abstract class ConicBundle::Coeffmat . The following versions of this abstract class are implemented so far and may be used directly as blocks
), each block being a coefficient matrix of the abstract class ConicBundle::Coeffmat . The following versions of this abstract class are implemented so far and may be used directly as blocks
- CMsymdense, a general purpose dense symmetric matrix building upon CH_Matrix_Classes::Symmatrix
- CMsymsparse, a sparse symmetric matrix building upon CH_Matrix_Classes::Sparsesym
- CMgramdense, a matrix
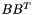 with
with 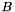 a dense rectangular CH_Matrix_Classes::Matrix
a dense rectangular CH_Matrix_Classes::Matrix - CMgramsparse, a matrix
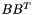 with
with 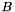 a sparse rectangular CH_Matrix_Classes::Sparsemat
a sparse rectangular CH_Matrix_Classes::Sparsemat - CMgramsparse_withoutdiag, a matrix
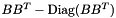 for a rectangular CH_Matrix_Classes::Sparsemat (useful in some quadratic 0-1 constraint representations)
for a rectangular CH_Matrix_Classes::Sparsemat (useful in some quadratic 0-1 constraint representations) - CMsingleton, a symmetric matrix with just one nonzero entry (by symmetry two if not on the diagonal)
- CMlowrankdd, a matrix
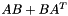 with each of
with each of 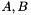 a dense rectangular CH_Matrix_Classes::Matrix
a dense rectangular CH_Matrix_Classes::Matrix - CMlowrankss, a matrix
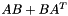 with each of
with each of 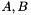 a sparse rectangular CH_Matrix_Classes::Sparsemat
a sparse rectangular CH_Matrix_Classes::Sparsemat - CMlowranksd, a matrix
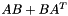 with
with 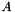 a sparse rectangular CH_Matrix_Classes::Sparsemat and
a sparse rectangular CH_Matrix_Classes::Sparsemat and 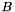 a dense rectangular CH_Matrix_Classes::Matrix
a dense rectangular CH_Matrix_Classes::Matrix
The block diagonal coefficient matrices 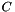 and
and 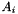 are each organized as instances of a ConicBundle::SparseCoeffmatMatrix which has the blocks as rows and each of its columns corresponds to one symmetric block matrix consisting of the corresponding diagonal blocks. In fact, it is more useful to think of the diagonal blocks
are each organized as instances of a ConicBundle::SparseCoeffmatMatrix which has the blocks as rows and each of its columns corresponds to one symmetric block matrix consisting of the corresponding diagonal blocks. In fact, it is more useful to think of the diagonal blocks 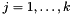 as corresponding to separate semidefinite variables
as corresponding to separate semidefinite variables 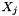 , so that for each block
, so that for each block 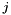 there are coefficient matrices
there are coefficient matrices 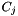 and
and 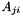 ,
, 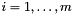 (many possibly of value zero)
(many possibly of value zero)
![\[ X=\left[\begin{array}{@{}c@{}c@{}c@{}} X_1 & & 0 \\[-1ex] & \ddots & \\[-.5ex] 0 & &X_k\end{array}\right],\quad C=\left[\begin{array}{@{}c@{}c@{}c@{}} C_1 & & 0 \\[-1ex] & \ddots & \\[-.5ex] 0 & &C_k\end{array}\right],\quad A_i=\left[\begin{array}{@{}c@{}c@{}c@{}} A_{1i} & & 0 \\[-1ex] & \ddots & \\[-.5ex] 0 & &A_{ki}\end{array}\right]~ (i=1,\dots,m), \]](form_343.png)
resulting in an SDP problem
![\[ \mbox{maximize }\sum_{j=1}^k\langle C_j,X_j\rangle \mbox{ subject to } \sum_{j=1}^k\langle -A_{ji},X_j\rangle \begin{array}{c}\le\\=\\\ge\end{array} b_i~ (i=1,\dots,m),~~ \sum_{j=1}^k\langle I,X_j\rangle \begin{array}{c}\le\\=\end{array}\gamma,~~ X_j\succeq 0~ (j=1,\dots,k)\]](form_344.png)
In this sense ConicBundle::SparseCoeffmatMatrix is simply a representation of a sparse matrix having a (pointer to a) matrix 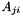 as element
as element 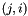 . In PSCAffineFunction this matrix is called opAt.
. In PSCAffineFunction this matrix is called opAt.
The standard use of an PSCAffineFunction is to fully initialize it on construction with matrices C and opAt of type SparseCoeffmatMatrix (and maybe a generating primal, see below) and then to add this function to the MatrixCBSolver by MatrixCBSolver::add_function(). If dynamic changes to this PSCAffineFunction are required afterwards, use the class ConicBundle::PSCAffineModification within the corresponding problem modification routines MatrixCBSolver::append_variables(), MatrixCBSolver::reassign_variables(), MatrixCBSolver::delete_variables() of the MatrixCBSolver interface.
In order to allow the solver (or rather PSCModel) to aggregate the eigenvector information to primal approximations of the primal semidefinite 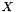 (or the semidefinite blocks
(or the semidefinite blocks 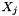 ), one may install a pointer to a generating PSCPrimal on construction or via applying PSCAffineModification::add_reset_generating_primal(). Several versions of PSCPrimal are implemented and ready to use:
), one may install a pointer to a generating PSCPrimal on construction or via applying PSCAffineModification::add_reset_generating_primal(). Several versions of PSCPrimal are implemented and ready to use:
- DensePSCPrimal, general purpose dense
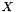 based on CH_Matrix_Classes::Symmatrix, this is only useful for small matrices or small blocks, but it also keeps all information.
based on CH_Matrix_Classes::Symmatrix, this is only useful for small matrices or small blocks, but it also keeps all information. - SparsePSCPrimal, it is initialized with a nonzero support structure and then the matrix entries are only collected on this support. The implementation is based on CH_Matrix_Classes::Sparsesym and is particularly useful if all matrices
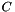 and
and 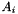 have a common small support, because then all inner products are formed correctly with this reduced support of the true
have a common small support, because then all inner products are formed correctly with this reduced support of the true 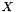 .
. - GramSparsePSCPrimal, this is tuned for best representing the current optimal solution of the bundle subproblem of the solver (or rather PSCModel) by a matrix of the form
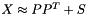 where
where 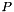 is the part due to the subspace description of the model and
is the part due to the subspace description of the model and 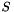 is the sparse part collected for the aggregate matrices of the model on a selected support as in SparsePSCPrimal.
is the sparse part collected for the aggregate matrices of the model on a selected support as in SparsePSCPrimal. - BlockPSCPrimal allows to represent the primal information of a diagonal block partition of the full
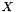 by any choice of an PSCPrimal, in particular the ones given before. if
by any choice of an PSCPrimal, in particular the ones given before. if 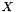 is itself a block matrix, typically the block partition of BlockPSCPrimal will be chosen to match the one of
is itself a block matrix, typically the block partition of BlockPSCPrimal will be chosen to match the one of 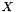 but it is not required to match. One main purpose in this choice is to allow inner products to work correctly for any new contraints
but it is not required to match. One main purpose in this choice is to allow inner products to work correctly for any new contraints 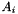 that are added dynamically.
that are added dynamically.
When the solver (or rather PSCModel) calls the implementation of PSCOracle::evaluate() for some 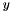 , PSCAffineFunction collects the affine matrix function
, PSCAffineFunction collects the affine matrix function 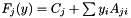 of each block
of each block 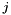 in a separate Bigmatrix, the latter is derived from a CH_Matrix_Classes::Lanczosmatrix so as to serve as input for the iterative Lanczos eigenvalue solver CH_Matrix_Classes::Lanczpol. Then PSCAffineFunction starts a separate eigensolver (but so far not in parallel) for the bigmatrix of each block. If the block is small, a standard eigenvalue method is used, otherwise the Lanczos method is employed. In any case the method will not only yield the maximum eigenvector (or a Ritz vector with sufficiently large Ritz value to ensure a null step), but several other Ritz vectors as well, that might help to improve the quality of the model in PSCModel. The routine PSCAffineFunction::set_max_Ritzvecs() allows to specify how many of the Ritz vectors should be passed on to PSCModel as a result of the call to PSCAffineFunction::evaluate().
in a separate Bigmatrix, the latter is derived from a CH_Matrix_Classes::Lanczosmatrix so as to serve as input for the iterative Lanczos eigenvalue solver CH_Matrix_Classes::Lanczpol. Then PSCAffineFunction starts a separate eigensolver (but so far not in parallel) for the bigmatrix of each block. If the block is small, a standard eigenvalue method is used, otherwise the Lanczos method is employed. In any case the method will not only yield the maximum eigenvector (or a Ritz vector with sufficiently large Ritz value to ensure a null step), but several other Ritz vectors as well, that might help to improve the quality of the model in PSCModel. The routine PSCAffineFunction::set_max_Ritzvecs() allows to specify how many of the Ritz vectors should be passed on to PSCModel as a result of the call to PSCAffineFunction::evaluate().
For facilitating input and output PSCAffineFunction offers
- PSCAffineFunction::print_problem_data() that outputs the full function description so that it can be read again by read_problem_data
- PSCAffineFunction::read_problem_data() reads the problem data as output by print_problem_data()
- PSCAffineFunction::set_out() and PSCAffineFunction::set_cbout() work as described in ConicBundle::CBout
Enumeration Type Documentation
◆ Coeffmattype
for recognizing the type when writing and reading the problem
| Enumerator | |
|---|---|
| CM_unspec | any user defined constraint may use this |
| CM_symdense | for CMsymdense |
| CM_symsparse | for CMsymsparse |
| CM_lowrankdd | for CMlowrankdd |
| CM_lowranksd | for CMlowranksd |
| CM_lowrankss | for CMlowrankss |
| CM_gramdense | for CMgramdense |
| CM_gramsparse | for CMgramsparse |
| CM_singleton | for CMsingleton |
| CM_gramsparsewd | |
Function Documentation
◆ apply_modification()
|
virtual |
see PSCOracle::apply_modification() for the general use, here oracle_modification has a special role if it can be cast to an PSCAffineModification
if oracle_modification cannot be cast to an PSCAffineModification it is assumed that all append modifications amount to have already been carried out on *this seperately before this routine is called. In particular, it is only checked whether the new dimension matches the one given by oracle_modification, the old dimension is ignored. If this does not hold, the routine stops with an error. Otherwise it checks the other stuff as if a suitable PSCAffineModification has just been executed.
Reimplemented from ConicBundle::PSCOracle.
◆ extend()
|
virtual |
called by ConicBundle to update internal Minorant objects, has to return 0 on success
- Parameters
-
[in,out] minorant (Minorant&) it holds a (possibly aggregated) minorant that was generated from minorants returned by oracle calls, e.g. as in FunctionOracle::evaluate() If PrimalData was provided in these minorants, this will be aggregated along and will also be available in this minorant. [in] n_coords (int) the number of coordinate positions that have to be filled in [out] indices (const int*) the indices of these coordinate positions (sorted in strictly increasing order)
- Returns
- 0 on success,
- 1 if extension is impossible
Implements ConicBundle::MinorantExtender.
◆ get_C()
|
inline |
returns the block representation of the coefficient matrices (each entry of the map represents a block by a SparseCoeffmatVector).
Referenced by ConicBundle::PSCModel::QPPSCOracleData::get_C().
◆ get_opAt()
|
inline |
returns the row representation of the coefficient matrices (each entry of the map represents a row by a SparseCoeffmatVector).
Referenced by ConicBundle::PSCModel::QPPSCOracleData::get_opAt().
◆ PSCAffineFunction()
| ConicBundle::PSCAffineFunction::PSCAffineFunction | ( | const SparseCoeffmatMatrix & | C, |
| const SparseCoeffmatMatrix & | opAt, | ||
| PSCPrimal * | generating_primal = 0, |
||
| const CBout * | cb = 0, |
||
| int | incr = -1 |
||
| ) |
initialize the PSCAffineFunction with its matrices and possible a generating_primal
C and opAt define the constant (block-)offset and the linear (block-)matrix function as described in the general text of PSCAffineFunction
generating_primal defines in what form primal matrices should be aggregated. If the argument is NULL then no primal aggregation will take place. The control over the generating primal is passed over to this. This will delete an existing generating primal whenever a new generating primal is set or upon destruction.
The final two arguments allow to set the output, see CBout.
◆ set_check_correctness()
|
inline |
set the maximum number of Ritz vectors returned in evaluate(), see implemention of a PSCOracle (PSCAffineFunction)
if set to true, ConicBundle employs some additional consistency checks
 1.8.13
1.8.13