defines a base class for coefficient matrices in semidefinite programming, in particular for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction). More...
#include <Coeffmat.hxx>
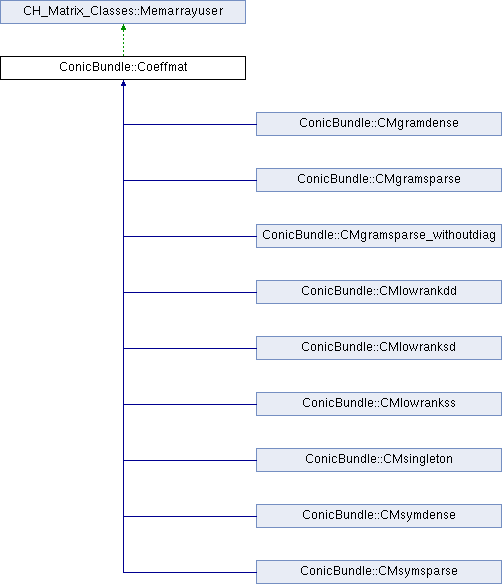
Inheritance diagram for ConicBundle::Coeffmat:
Public Member Functions | |
| Coeffmat (bool del_by_CoeffmatPointer=true) | |
| default constructor; set del_by_CoeffmatPointer==true if a CoeffmatPointer reducing the use_cnt to zero should delete this | |
| void | set_deletion_by_CoeffmatPointer (bool dbMP) |
| if set to true any CoeffmatPointer that reduces use_cnt to zero will delete this object | |
| virtual Coeffmattype | get_type () const |
| returns its Coeffmattype | |
| virtual CoeffmatInfo * | get_info () |
| returns the user information | |
| virtual const CoeffmatInfo * | get_info () const |
| returns the user information in const form | |
| virtual void | set_info (CoeffmatInfo *cip) |
| deletes the old and sets new user information | |
| virtual Coeffmat * | clone () const =0 |
| makes an explicit copy of itself and returns a pointer to it | |
| virtual CH_Matrix_Classes::Integer | dim () const =0 |
| returns the order of the represented symmetric matrix | |
| virtual CH_Matrix_Classes::Real | operator() (CH_Matrix_Classes::Integer i, CH_Matrix_Classes::Integer j) const =0 |
| returns the value of the matrix element (i,j) | |
| virtual void | make_symmatrix (CH_Matrix_Classes::Symmatrix &S) const =0 |
| returns a dense symmetric constraint matrix (useful for testing) | |
| virtual CH_Matrix_Classes::Real | norm (void) const =0 |
| returns the Frobenius norm of the matrix | |
| virtual Coeffmat * | subspace (const CH_Matrix_Classes::Matrix &P) const =0 |
| delivers a new object on the heap corresponding to the matrix P^TAP, the caller is responsible for deleting the object | |
| virtual void | multiply (CH_Matrix_Classes::Real d)=0 |
| multiply constraint permanentely by d; this is to allow scaling or sign changes in the constraints | |
| virtual CH_Matrix_Classes::Real | ip (const CH_Matrix_Classes::Symmatrix &S) const =0 |
| returns ip(*this,S)=trace(*this*S), the trace inner product | |
| virtual CH_Matrix_Classes::Real | gramip (const CH_Matrix_Classes::Matrix &P) const =0 |
| returns ip(*this,PP^T)=trace P^T(*this)P | |
| virtual CH_Matrix_Classes::Real | gramip (const CH_Matrix_Classes::Matrix &P, CH_Matrix_Classes::Integer start_row, const CH_Matrix_Classes::Matrix *Lam=0) const =0 |
| returns ip(*this,Q*Diag(Lam)*Q^T)=trace Q^T(*this)Q*Diag(Lam) for Q=P.rows(start_row,start_row+dim-1), where Diag(Lam) is the identity if not given | |
| virtual void | addmeto (CH_Matrix_Classes::Symmatrix &S, CH_Matrix_Classes::Real d=1.) const =0 |
| computes S+=d*(*this); | |
| virtual void | addprodto (CH_Matrix_Classes::Matrix &A, const CH_Matrix_Classes::Matrix &B, CH_Matrix_Classes::Real d=1.) const =0 |
| comutes A+=d*(*this)*B | |
| virtual void | addprodto (CH_Matrix_Classes::Matrix &A, const CH_Matrix_Classes::Sparsemat &B, CH_Matrix_Classes::Real d=1.) const =0 |
| computes A+=d*(*this)*B | |
| virtual void | left_right_prod (const CH_Matrix_Classes::Matrix &P, const CH_Matrix_Classes::Matrix &Q, CH_Matrix_Classes::Matrix &R) const =0 |
| computes R=P^T*(*this)*Q | |
| virtual CH_Matrix_Classes::Integer | prodvec_flops () const =0 |
| returns an estimate of number of flops to compute addprodto for a vector | |
| virtual int | dense () const =0 |
| returns 1 if its structure is as bad as its dense symmetric representation, otherwise 0 | |
| virtual int | sparse () const =0 |
| returns 0 if not sparse, otherwise 1 | |
| virtual int | sparse (CH_Matrix_Classes::Indexmatrix &I, CH_Matrix_Classes::Indexmatrix &J, CH_Matrix_Classes::Matrix &val, CH_Matrix_Classes::Real d=1.) const =0 |
| returns 0 if not sparse. If it is sparse it returns 1 and the nonzero structure in I,J and val, where val is multiplied by d. Only the upper triangle (including diagonal) is delivered | |
| virtual int | support_in (const CH_Matrix_Classes::Sparsesym &A) const =0 |
| returns 0 if the support of the costraint matrix is not contained in the support of the sparse symmetric matrix A, 1 if it is contained. | |
| virtual CH_Matrix_Classes::Real | ip (const CH_Matrix_Classes::Sparsesym &A) const =0 |
| returns the inner product of the constraint matrix with A | |
| virtual void | project (CH_Matrix_Classes::Symmatrix &S, const CH_Matrix_Classes::Matrix &P) const =0 |
| computes S=P^T*(*this)*P | |
| virtual void | add_projection (CH_Matrix_Classes::Symmatrix &S, const CH_Matrix_Classes::Matrix &P, CH_Matrix_Classes::Real alpha=1., CH_Matrix_Classes::Integer start_row=0) const =0 |
| computes S+=alpha*Q^T(*this)Q for Q=P.rows(start_row,start_row+dim-1) | |
| virtual const CH_Matrix_Classes::Matrix & | postgenmult (const CH_Matrix_Classes::Matrix &B, CH_Matrix_Classes::Matrix &C, CH_Matrix_Classes::Real alpha=1., CH_Matrix_Classes::Real beta=0., int btrans=0) const =0 |
| computes C= alpha*(*this)*B^(T if btrans) + beta*C, C is also returned | |
| virtual const CH_Matrix_Classes::Matrix & | pregenmult (const CH_Matrix_Classes::Matrix &B, CH_Matrix_Classes::Matrix &C, CH_Matrix_Classes::Real alpha=1., CH_Matrix_Classes::Real beta=0., int btrans=0) const =0 |
| computes C= alpha*B^(T if btrans)*(*this) + beta*C, C is also returned | |
| virtual int | equal (const Coeffmat *p, double tol=1e-6) const =0 |
| returns 1, if p is the same derived class and entries differ by less than tol, otherwise zero | |
| virtual std::ostream & | display (std::ostream &o) const =0 |
| display constraint information | |
| virtual std::ostream & | out (std::ostream &o) const =0 |
| put entire contents onto outstream with the class type in the beginning so that the derived class can be recognized by in(). | |
| virtual std::istream & | in (std::istream &i)=0 |
| counterpart to out(), does not read the class type, though. This is assumed to have been read in order to generate the correct class | |
Protected Attributes | |
| Coeffmattype | CM_type |
| in order to enable type identification | |
| CoeffmatInfo * | infop |
| allows the user to specify and output additional information | |
Private Attributes | |
| CH_Matrix_Classes::Integer | use_cnt |
| Each CoeffmatPointer pointing to his increase the use_cnt by one and it reduces it by one once it stops pointing to it; if use_cnt turns zero and deletion_by_CoeffmatPointer is true, the object will be deleted by the respective CoeffmatPointer. | |
| bool | deletion_by_CoeffmatPointer |
| set deletion_by_CoeffmatPointer==true if a CoeffmatPointer reducing the use_cnt to zero should delete this | |
Friends | |
| class | CoeffmatPointer |
Additional Inherited Members | |
 Protected Member Functions inherited from CH_Matrix_Classes::Memarrayuser | |
| Memarrayuser () | |
| if memarray is NULL, then a new Memarray is generated. In any case the number of users of the Memarray is incremented | |
| virtual | ~Memarrayuser () |
| the number of users is decremented and the Memarray memory manager is destructed, if the number is zero. | |
| Static Protected Attributes inherited from CH_Matrix_Classes::Memarrayuser | |
| static Memarray * | memarray |
| pointer to common memory manager for all Memarrayusers, instantiated in memarray.cxx | |
Detailed Description
defines a base class for coefficient matrices in semidefinite programming, in particular for use with MatrixSDPfunction, see implemention of a PSCOracle (PSCAffineFunction).
The class supports several different needs, e.g. it should work well with the requirements of MaxEigOracle as well as those of the eigenvalue computations with Bigmatrix. Furthermore there is support for writing and reading the various implementations.
The documentation for this class was generated from the following file:
