AffineMatrixFunction needs to compute the maximum eigenvalue of an affine matrix function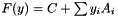 
. This class prepares 
in useful form for iterative eigenvalue solvers.
More...
#include <Bigmatrix.hxx>
Inheritance diagram for ConicBundle::Bigmatrix:
Public Member Functions | |
| void | clear () |
| clear all data | |
| CH_Matrix_Classes::Integer | get_nmult () const |
| return number of matrix vector products | |
| void | reset_nmult () |
| reset the counter of matrix vector products to zero | |
| int | init (const CH_Matrix_Classes::Matrix &yi, CH_Matrix_Classes::Integer indim, const CoeffmatPointer C, const SparseCoeffmatVector *Ai, const bool dense=false) |
| compute a good representation of 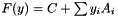(if dense==true directly a dense one) | |
| void | set_tol (CH_Matrix_Classes::Real t) |
| sets the tolerance for considering computed values as zeros | |
| int | get_dense () const |
| return true if a dense representation was computed | |
| virtual CH_Matrix_Classes::Integer | lanczosdim () const |
| the order of the matrix as required by CH_Matrix_Classes::Lanczosmatrix | |
| virtual CH_Matrix_Classes::Integer | lanczosflops () const |
| the estimated flop count of a matrix vector multiplication as required by CH_Matrix_Classes::Lanczosmatrix | |
| virtual int | lanczosmult (const CH_Matrix_Classes::Matrix &A, CH_Matrix_Classes::Matrix &B) const |
| computes B = bigMatrix * A (A and B must not refer to the same memory) as required by CH_Matrix_Classes::Lanczosmatrix | |
| int | make_symmatrix (CH_Matrix_Classes::Symmatrix &S) const |
| write a dense version of the current matrix to S | |
| const CH_Matrix_Classes::Symmatrix & | get_symrep () const |
| compute the dense version locally and return a reference to it | |
Private Types | |
| typedef std::map< CH_Matrix_Classes::Integer, CH_Matrix_Classes::Real > | Indexhash |
| for collecting the indices of sparse data this seems useful | |
Private Attributes | |
| CH_Matrix_Classes::Real | tol |
| tolerance for considering an element to be zero | |
| CH_Matrix_Classes::Integer | dim |
| size of the matrix | |
| CH_Matrix_Classes::Integer | nz |
| total number of nonzeros (except diagonal) | |
| CH_Matrix_Classes::Indexmatrix | colnz |
| nonzeros of each column | |
| std::vector< CH_Matrix_Classes::Indexmatrix > | rowind |
| nonzero row indices in each column | |
| std::vector< CH_Matrix_Classes::Matrix > | rowval |
| corresponding nonzero row values | |
| CH_Matrix_Classes::Matrix | di |
| diagonal elements | |
| std::vector< Indexhash > | rowhash |
| for finding nonzero indices | |
| std::vector< CoeffmatPointer > | mcp |
| pointers to dense matrices | |
| CH_Matrix_Classes::Matrix | mcv |
| multiplier values for the dense matrices | |
| CH_Matrix_Classes::Integer | nmult |
| counts the number of Mat*vec operations | |
| bool | use_dense |
| usually false, set to true if matrix is sufficiently dense | |
| CH_Matrix_Classes::Symmatrix | symrep |
| if use_dense is true, the matrix is stored here | |
| bool | symrep_init |
| flag whether symrep is computed already | |
| CH_Matrix_Classes::Matrix | At |
| auxilliary variable used in matrix vector products | |
| CH_Matrix_Classes::Matrix | Bt |
| auxilliary variable used in matrix vector products | |
| CH_Matrix_Classes::Indexmatrix | collecti |
| for collecting the sparse part | |
| CH_Matrix_Classes::Indexmatrix | collectj |
| for collecting the sparse part | |
| CH_Matrix_Classes::Matrix | collectval |
| for collecting the sparse part | |
Friends | |
| std::ostream & | operator<< (std::ostream &out, const Bigmatrix &) |
| output information | |
Additional Inherited Members | |
 Protected Member Functions inherited from CH_Matrix_Classes::Memarrayuser | |
| Memarrayuser () | |
| if memarray is NULL, then a new Memarray is generated. In any case the number of users of the Memarray is incremented | |
| virtual | ~Memarrayuser () |
| the number of users is decremented and the Memarray memory manager is destructed, if the number is zero. | |
| Static Protected Attributes inherited from CH_Matrix_Classes::Memarrayuser | |
| static Memarray * | memarray |
| pointer to common memory manager for all Memarrayusers, instantiated in memarray.cxx | |
Detailed Description
AffineMatrixFunction needs to compute the maximum eigenvalue of an affine matrix function 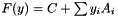. This class prepares 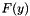in useful form for iterative eigenvalue solvers.
In AffineMatrixFunction the matrices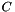 
and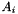 
are of type Coeffmat, the information provided by these matrices is used to decide which parts should be represented in a sparse form and which parts in a dense form. The intention is that in the end matrix vector products can be computed efficiently, so that e.g. a Lanczcos algorithm can be used. For this purpose Bigmatrix is a publically derived CH_Matrix_Classes::Lanczosmatrix.
The documentation for this class was generated from the following file:
