implements a sparse symmetric PSCPrimal collecting data only on a sparse, prespecified support; it is based on CH_Matrix_Classes::Sparsesym More...
#include <PSCPrimal.hxx>
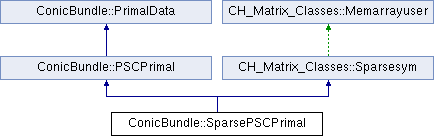
Inheritance diagram for ConicBundle::SparsePSCPrimal:
Public Member Functions | |
| SparsePSCPrimal (const CH_Matrix_Classes::Sparsesym &sps, double factor=1.) | |
| copy constructor from a CH_Matrix_Classes::Sparssym, only the support of this matrix will be used in all Gram operations | |
| SparsePSCPrimal (const SparsePSCPrimal &pr, double factor=1.) | |
| copy constructor, only the same support will be used in all Gram operations | |
| SparsePSCPrimal & | operator= (const CH_Matrix_Classes::Sparsesym &sdp) |
| assigns this Sparsesym, only the same support will be used in all Gram operations | |
| PrimalData * | clone_primal_data () const |
| returns a newly generated identical Object | |
| int | assign_Gram_matrix (const CH_Matrix_Classes::Matrix &P) |
| for each element aij in the support set aij=<P.row(i),P.row(j)> | |
| int | aggregate_primal_data (const PrimalData &it, double factor=1.) |
| if it is a SparseSDPRimal, add factor*it to this on the support of this | |
| int | aggregate_Gram_matrix (const CH_Matrix_Classes::Matrix &P, double factor=1.) |
| add factor*P*P^T on the support to this | |
| virtual int | scale_primal_data (double factor) |
| multiply/scale *this with a nonnegative factor | |
| virtual int | primal_ip (CH_Matrix_Classes::Real &value, const SparseCoeffmatMatrix &A, CH_Matrix_Classes::Integer column) const |
| if compatible evaluate value=ip(*this,A.column[i]) | |
 Public Member Functions inherited from CH_Matrix_Classes::Sparsesym | |
| Sparsesym () | |
| empty matrix | |
| Sparsesym (const Sparsesym &A, Real d=1.) | |
| copy constructor, *this=d*A | |
| Sparsesym (Integer nr) | |
| initialize to zero-matrix of size nr*nr | |
| Sparsesym (Integer nr, Integer nz, const Integer *ini, const Integer *inj, const Real *va) | |
| initialize to size nr*nr and nz nonzeros so that this(ini[i],inj[i])=val[i] for i=0,..,nz-1; specify only one of (i,j) and (j,i), multiple elements are summed up. | |
| Sparsesym (Integer nr, Integer nz, const Indexmatrix &ini, const Indexmatrix &inj, const Matrix &va) | |
| initialize to size nr*nr and nz nonzeros so that this(ini(i),inj(i))=val[i] for i=0,..,nz-1; specify only one of (i,j) and (j,i), multiple elements are summed up. | |
| void | set_init (bool) |
| after external initialization, call matrix.set_init(true) (not needed if CONICBUNDLE_DEBUG is undefined) | |
| bool | get_init () const |
| returns true if the matrix has been declared initialized (not needed if CONICBUNDLE_DEBUG is undefined) | |
| Sparsesym & | init (const Sparsesym &, Real d=1.) |
| initialize to *this=A*d | |
| Sparsesym & | init (const Matrix &, Real d=1.) |
| initialize to this=d(A+transpose(A))/2., abs(values)<tol are removed from the support | |
| Sparsesym & | init (const Indexmatrix &, Real d=1.) |
| initialize to this=d(A+transpose(A))/2., zeros are removed from the support | |
| Sparsesym & | init (const Symmatrix &, Real d=1.) |
| initialize to *this=A*d, abs(values)<tol are removed from the support | |
| Sparsesym & | init (const Sparsemat &, Real d=1.) |
| initialize to this=d(A+transpose(A))/2. | |
| Sparsesym & | init (Integer nr) |
| initialize to zero-matrix of size nr*nr | |
| Sparsesym & | init (Integer nr, Integer nz, const Integer *ini, const Integer *inj, const Real *va) |
| initialize to size nr*nr and nz nonzeros so that this(ini[i],inj[i])=val[i] for i=0,..,nz-1; specify only one of (i,j) and (j,i), multiple elements are summed up. | |
| Sparsesym & | init (Integer nr, Integer nz, const Indexmatrix &ini, const Indexmatrix &inj, const Matrix &va) |
| initialize to size nr*nr and nz nonzeros so that this(ini(i),inj(i))=val[i] for i=0,..,nz-1; specify only one of (i,j) and (j,i), multiple elements are summed up. | |
| Sparsesym & | init_support (const Sparsesym &A, Real d=0.) |
| void | set_tol (Real t) |
| set tolerance for recognizing zero values to t | |
| Sparsesym (const Matrix &, Real d=1.) | |
| initialize to this=d(A+transpose(A))/2., abs(values)<tol are removed from the support | |
| Sparsesym (const Indexmatrix &, Real d=1.) | |
| initialize to this=d(A+transpose(A))/2., zeros are removed from the support | |
| Sparsesym (const Symmatrix &, Real d=1.) | |
| initialize to *this=A*d, abs(values)<tol are removed from the support | |
| Sparsesym (const Sparsemat &, Real d=1.) | |
| initialize to this=d(A+transpose(A))/2. | |
| void | dim (Integer &r, Integer &c) const |
| returns the number of rows in _nr and the number of columns in _nc | |
| Integer | dim () const |
| returns the dimension rows * columns when the matrix is regarded as a vector | |
| Integer | rowdim () const |
| returns the row dimension | |
| Integer | coldim () const |
| returns the column dimension | |
| Integer | nonzeros () const |
| returns the number of nonzeros in the lower triangle (including diagonal) | |
| Mtype | get_mtype () const |
| returns the type of the matrix, MTmatrix | |
| Real | operator() (Integer i, Integer j) const |
| returns value of element (i,j) of the matrix (rowindex i, columnindex j) | |
| Real | operator() (Integer i) const |
| returns value of element (i) of the matrix if regarded as vector of stacked columns [element (irowdim, i/rowdim)] | |
| Real | operator[] (Integer i) const |
| returns value of element (i) of the matrix if regarded as vector of stacked columns [element (irowdim, i/rowdim)] | |
| const Indexmatrix & | get_colinfo () const |
| returns information on nozero diagonal/columns, k by 4, listing: index (<0 for diagonal), # nonzeros, first index in colindex/colval, index in suppport submatrix | |
| const Indexmatrix & | get_colindex () const |
| returns the index vector of the column representation holding the row index for each element | |
| const Matrix & | get_colval () const |
| returns the value vector of the column representation holding the value for each element | |
| const Indexmatrix & | get_suppind () const |
| returns the index vector of the column representation holding the row index w.r.t. the principal support submatrix for each element | |
| const Indexmatrix & | get_suppcol () const |
| returns the vector listing in ascending order the original column indices of the principal support submatrix | |
| void | get_edge_rep (Indexmatrix &I, Indexmatrix &J, Matrix &val) const |
| stores the nz nonzero values of the lower triangle of *this in I,J,val so that this(I(i),J(i))=val(i) for i=0,...,nz-1 and dim(I)=dim(J)=dim(val)=nz (ordered as in row representation) | |
| int | contains_support (const Sparsesym &A) const |
| returns 1 if A is of the same dimension and the support of A is contained in the support of *this, 0 otherwise | |
| int | check_support (Integer i, Integer j) const |
| returns 0 if (i,j) is not in the support, 1 otherwise | |
| Sparsesym & | xeya (const Sparsesym &A, Real d=1.) |
| sets *this=d*A and returns *this | |
| Sparsesym & | xeya (const Matrix &A, Real d=1.) |
| sets and returns this=d(A+transpose(A))/2. where abs(values)<tol are removed from the support | |
| Sparsesym & | xeya (const Indexmatrix &A, Real d=1.) |
| sets and returns this=d(A+transpose(A))/2. where zeros are removed from the support | |
| Sparsesym & | support_xbpeya (const Sparsesym &y, Real alpha=1., Real beta=0.) |
| returns this= alpha*y+beta(*this) restricted to the curent support of *this; if beta==0, then *this is initialized to 0 on its support first | |
| Sparsesym & | operator= (const Sparsesym &A) |
| Sparsesym & | operator+= (const Sparsesym &v) |
| Sparsesym & | operator-= (const Sparsesym &v) |
| Sparsesym | operator- () const |
| Sparsesym & | operator*= (Real d) |
| Sparsesym & | operator/= (Real d) |
| ATTENTION: d is NOT checked for 0. | |
| Sparsesym & | operator= (const Matrix &A) |
| sets *this=(A+transpose(A))/2. removing abs(values)<tol; returns *this | |
| Sparsesym & | operator= (const Indexmatrix &A) |
| sets *this=(A+transpose(A))/2. removing zeros; returns *this | |
| Sparsesym & | transpose () |
| transposes itself (at almost no cost) | |
| Sparsesym & | xeya (const Symmatrix &A, Real d=1.) |
| sets and returns *this=A*d where abs(values)<tol are removed from the support | |
| Sparsesym & | xeya (const Sparsemat &A, Real d=1.) |
| sets and returns this=d.(A+transpose(A))/2. | |
| Sparsesym & | operator= (const Symmatrix &A) |
| sets and returns *this=A where abs(values)<tol are removed from the support | |
| Symmatrix | operator+ (const Symmatrix &A) const |
| Symmatrix | operator- (const Symmatrix &A) const |
| Sparsesym & | operator= (const Sparsemat &A) |
| sets and returns *this=(A+transpose(A))/2. | |
| Sparsemat | sparsemult (const Matrix &A) const |
| compute (*this)*A and return the result in a Sparsemat | |
| void | display (std::ostream &out, int precision=0, int width=0, int screenwidth=0) const |
| displays a matrix in a pretty way for bounded screen widths; for variables of value zero default values are used. More... | |
Additional Inherited Members | |
| Protected Member Functions inherited from CH_Matrix_Classes::Memarrayuser | |
| Memarrayuser () | |
| if memarray is NULL, then a new Memarray is generated. In any case the number of users of the Memarray is incremented | |
| virtual | ~Memarrayuser () |
| the number of users is decremented and the Memarray memory manager is destructed, if the number is zero. | |
| Static Protected Attributes inherited from CH_Matrix_Classes::Memarrayuser | |
| static Memarray * | memarray |
| pointer to common memory manager for all Memarrayusers, instantiated in memarray.cxx | |
Detailed Description
implements a sparse symmetric PSCPrimal collecting data only on a sparse, prespecified support; it is based on CH_Matrix_Classes::Sparsesym
SparsePSCPrimal is pubically derived from PSCPrimal and CH_Matrix_Classes::Sparseym, so it may be used directly like a sparse symmetric matrix
The documentation for this class was generated from the following file:
