Oracle interface for minimization of the maximum eigenvalue of an affine matrix function or, equivalently, Lagrangian relaxation of semidefinite programs. More...

#include <PSCOracle.hxx>

Inheritance diagram for ConicBundle::PSCOracle:

Public Member Functions
virtual Minorant *	generate_minorant (const CH_Matrix_Classes::Matrix &P)=0
	generates the minorant that arises from the gram matrix PP^T (maybe including some primal information for primal aggregation). More...

virtual int	svec_projection (CH_Matrix_Classes::Matrix &svec_offset, CH_Matrix_Classes::Matrix &svec_coeffs, const CH_Matrix_Classes::Matrix &P, const CH_Matrix_Classes::Indexmatrix *index_subset=0)=0
	compute svec representation of the projected coefficient matrices More...

virtual int	evaluate (const CH_Matrix_Classes::Matrix &current_point, const CH_Matrix_Classes::Matrix &bundlevecs, const double relprec, const double Ritz_bound, CH_Matrix_Classes::Matrix &Ritz_vectors, CH_Matrix_Classes::Matrix &Ritz_values, PSCPrimalExtender *&primal_extender)=0

virtual int	evaluate_projection (const CH_Matrix_Classes::Matrix &current_point, const CH_Matrix_Classes::Matrix &P, const double relprec, CH_Matrix_Classes::Matrix &projected_Ritz_vectors, CH_Matrix_Classes::Matrix &projected_Ritz_values)=0

virtual int	left_right_product (int i, const CH_Matrix_Classes::Matrix &P, const CH_Matrix_Classes::Matrix &Q, CH_Matrix_Classes::Matrix &G)=0

virtual int	apply_modification (const OracleModification &, const CH_Matrix_Classes::Matrix , const CH_Matrix_Classes::Matrix , bool &, bool &, bool &, MinorantExtender *&)
	This routine need not be implemented unless variables (constraints in Lagrangean relaxation) are added or deleted on the fly. More...

virtual bool	check_correctness () const
	switch on/off some correctnes checks on the oracle

Public Member Functions inherited from ConicBundle::ModifiableOracleObject
virtual	~ModifiableOracleObject ()
	virtual destructor

Detailed Description

Oracle interface for minimization of the maximum eigenvalue of an affine matrix function or, equivalently, Lagrangian relaxation of semidefinite programs.

Within the setting explained in abstract positive semidefinite cone oracle the abstract class PSCOracle defines a matrix free interface to maximum eigenvalue/eigenvector and the action of the affine matrix function $C+\sum_{i=1}^my_iA_i$ for the spectral bundle cutting model implemented in PSCModel. In particular, it provides in

generate_minorant() the minorant corresponding to a gram matrix PP^T (maybe with additional primal data for primal aggregation)
svec_projection() the projection 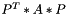onto a subspace spanned by 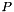for matrices 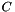and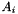
evaluate() for given 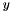the maximum eigenvalue/eigenvector of the affine matrix function or a Ritz_vector with sufficiently high Ritz_value to exceed the threshold for null steps in the bundle method
evaluate_projection() for given 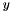the same as in evaluate but now for the projected affine matrix function 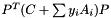$P^T(C+\sum y_iA_i)P$ where the columns in $P$ span the desired subspace
left_right_prod() the product 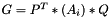for matrices 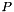and 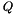(required for the bundle update and scaling heuristics in PSCModel)
and the function check_correctness() with the same meaning as in ConicBundle::FunctionOracle

For a concrete implementation of PSCOracle see ConicBundle::AffineMatrixFunction .

Member Function Documentation

◆ apply_modification()

virtual int ConicBundle::PSCOracle::apply_modification	(	const OracleModification &	,
		const CH_Matrix_Classes::Matrix *	,
		const CH_Matrix_Classes::Matrix *	,
		bool &	,
		bool &	,
		bool &	,
		MinorantExtender *&
	)

inlinevirtual

This routine need not be implemented unless variables (constraints in Lagrangean relaxation) are added or deleted on the fly.

The routine is only called by the solver if the variables indeed get modified by the solver or a modification is passed on by the user via the solver interface. oracle_modification is then used to either transfer user supplied instructions to the oracle on how to modify itself or to inform the oracle about changes the solver was asked to perform on the variables. If available, the solver will also show the effect of these changes on the center point in new_center and old_center; if these are not available then they hold NULL. A user supplied oracle_modification will be checked for consistency with the actual changes in the variables and mismatches will cause failures.

The remaining variables are output variables by which the oracle tells the solver which information has a chance to be preserved in view of these changes. If e.g. the deletion of some nonzero variables invalidates the function value in the new center, the oracle has to set discard_objective_in_center=true. If the entire model cannot be preserved (this includes the aggregates and the function values), the oracle needs to set discard_model=true; If only aggregate minorants cannot be preserved, the oracle needs to set discard_aggregates=true; in the current implementation of PSCModel this removes all minorants generated by generate_minorant() because each of them is typically generated by more than one Ritz vector. Whenever new variables were added, the model can only be preserved if the remaining minorants (maybe without aggregates) can be extended for these new variables. In this case the oracle has to supply the appropriate MinorantExtender via minorant_extender and only those minorants will be kept for which this operation succeeds.

Return value 0 indicates that these actions allow to continue without errors, other return values result in an overall error on these changes.

Reimplemented from ConicBundle::ModifiableOracleObject.

Reimplemented in ConicBundle::PSCAffineFunction.

◆ evaluate()

virtual int ConicBundle::PSCOracle::evaluate	(	const CH_Matrix_Classes::Matrix &	current_point,
		const CH_Matrix_Classes::Matrix &	bundlevecs,
		const double	relprec,
		const double	Ritz_bound,
		CH_Matrix_Classes::Matrix &	Ritz_vectors,
		CH_Matrix_Classes::Matrix &	Ritz_values,
		PSCPrimalExtender *&	primal_extender
	)

pure virtual

compute maximum eigenvalue of the matrix C+opAt(y)

Returns: 0 on success

Parameters

current_point	argument = current variables = position where to evaluate the function
bundlevecs	The columns of the matrix are orthonormal bundle vectors and may help to construct good startig vectors for the eigenvalue computation by iterative methods but have no other use. bundlevecs may have dimension 0.
relprec	relative precision requirement for objective values leading to descent steps
Ritz_bound	gives the threshold for a null step; a vector is good enough to yield sufficient improvement if its Ritz value exceeds this Ritz_bound. Otherwise the largest of the returned Ritz_values must be guaranteed to lie within relprec*(max(abs(Ritz_bound),1.)) of the maximum eigenvalue
Ritz_vectors	on input: if not zero dimensional, the columns of the matrix contains the orthonormal family of Ritz_vectors returned in the previous call; these may help to construct good starting vectors for the eigenvalue computation by iterative methods.

on output: the columns of the matrix form an orthonormal family that has to contain at least one vector 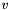$v$ with the following property: 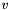$v$ is an eigenvector to the maximum eigenvalue or it has a Ritz value 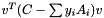$v^T(C-\sum y_iA_i)v$ that exceeds the null step bound Ritz_bound.

Parameters

	Ritz_values	Ritz_values corresponding to the Ritz_vectors
	primal_extender
[out]	primal_extender	(PrimalExtender*&) if primal_data or Ritz_vectors provided in minonrants of previous calls now have to be updated due to changes in the primal problem – e.g., this may happen in column generation – one may return a pointer to a PSCPrimalExtender object on the heap. This object will be used by ConicBundle to update all its internally stored Ritz_vectors and primal_data objects in its minorants by calling PrimalExtender::extend on each of these. Afterwards ConicBundle deletes primal_extender. If this is not needed, set the variable to NULL.

Implemented in ConicBundle::PSCAffineFunction.

◆ evaluate_projection()

virtual int ConicBundle::PSCOracle::evaluate_projection	(	const CH_Matrix_Classes::Matrix &	current_point,
		const CH_Matrix_Classes::Matrix &	P,
		const double	relprec,
		CH_Matrix_Classes::Matrix &	projected_Ritz_vectors,
		CH_Matrix_Classes::Matrix &	projected_Ritz_values
	)

pure virtual

compute maximum eigenvalue of P^T(C-opAt(y))P

Returns: 0 on success

Parameters

current_point	argument = current variable values = position where to evaluate the function
P	orthogonal matrix defining the projection;
relprec	relative precision requirement
projected_Ritz_vectors	output: orthognal matrix that contains at least one column vector that is an eigenvector to the maximum eigenvalue of the projected Matrix
projected_Ritz_values	output: Ritz_values corresponding to the Ritz_vectors

Implemented in ConicBundle::PSCAffineFunction.

◆ generate_minorant()

virtual Minorant* ConicBundle::PSCOracle::generate_minorant ( const CH_Matrix_Classes::Matrix & P )

pure virtual

generates the minorant that arises from the gram matrix PP^T (maybe including some primal information for primal aggregation).

The returned minorant must satisfy offset_gives_value_at_origin()==true. The minorant is passed over to the caller and will be deleted there.

Implemented in ConicBundle::PSCAffineFunction.

◆ left_right_product()

virtual int ConicBundle::PSCOracle::left_right_product	(	int	i,
		const CH_Matrix_Classes::Matrix &	P,
		const CH_Matrix_Classes::Matrix &	Q,
		CH_Matrix_Classes::Matrix &	G
	)

pure virtual

fills row i with vec(P^T*(A_i)*Q)^T (needed for the bundle update and the scaling heuristic in PSCModel)

Returns: 0 on success

Parameters

i	index of the coefficient matrix
P	left multiplication matrix
Q	right multiplication matrix
G	the result is stored in this matrix.

Implemented in ConicBundle::PSCAffineFunction.

◆ svec_projection()

virtual int ConicBundle::PSCOracle::svec_projection	(	CH_Matrix_Classes::Matrix &	svec_offset,
		CH_Matrix_Classes::Matrix &	svec_coeffs,
		const CH_Matrix_Classes::Matrix &	P,
		const CH_Matrix_Classes::Indexmatrix *	index_subset = `0`
	)

pure virtual

compute svec representation of the projected coefficient matrices

This always includes the constant cofficient matrix, svec_offset=svec(P^T*C*P). If index_subset==0, row i of svec_coeffs is filled with svec(P^T*A_i*P)^T for i=1,dots,m If index_subset!=0, row i of svec_coeffs holds this for A_{(*index_subset)(i)}

Implemented in ConicBundle::PSCAffineFunction.

The documentation for this class was generated from the following file:

PSCOracle.hxx

Public Member Functions

Detailed Description

Member Function Documentation

◆ apply_modification()

◆ evaluate()

◆ evaluate_projection()

◆ generate_minorant()

◆ left_right_product()

◆ svec_projection()