represents an PSCPrimal as the sum 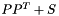$PP^T+S$ of a Gram matrix and a sparse symmetric matrix 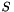$S$ More...

#include <PSCPrimal.hxx>

Inheritance diagram for ConicBundle::GramSparsePSCPrimal:

Public Member Functions
	GramSparsePSCPrimal (const CH_Matrix_Classes::Sparsesym &sps, double factor=1.)
	initialize to the given sparse symmetric matrix, the gram part is zero

	GramSparsePSCPrimal (const GramSparsePSCPrimal &pr, double factor=1.)
	copy constructor

GramSparsePSCPrimal &	operator= (const CH_Matrix_Classes::Sparsesym &sdp)
	assign the sparse symmetric matrix to this and set the gram part to zero

GramSparsePSCPrimal &	operator= (const GramSparsePSCPrimal &sdp)
	copy the information

const CH_Matrix_Classes::Matrix &	get_grammatrix () const
	returns the matrix 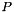giving rise to the Gram matrix

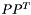PrimalData *	clone_primal_data () const
	returns a newly generated identical Object

int	assign_Gram_matrix (const CH_Matrix_Classes::Matrix &P)
	Set the grammatrix part to 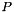and set all values on the sparse support to zero (but keep this support even if it is zero now!)

int	aggregate_primal_data (const PrimalData &it, double factor=1.)
	if it is a GramSparsePSCPrimal or SparseSDPRimal, add factor*it to this on only the support of this sparsematrix More...

int	aggregate_Gram_matrix (const CH_Matrix_Classes::Matrix &P, double factor=1.)
	add factorPP^T to this, collecting all available information only in the sparse part, even the own Gram part. More...

virtual int	scale_primal_data (double factor)
	multiply/scale *this with a nonnegative factor

virtual int	primal_ip (CH_Matrix_Classes::Real &value, const SparseCoeffmatMatrix &A, CH_Matrix_Classes::Integer column) const
	if compatible evaluate value=ip(*this,A.column[i])

Public Member Functions inherited from CH_Matrix_Classes::Sparsesym
	Sparsesym ()
	empty matrix

	Sparsesym (const Sparsesym &A, Real d=1.)
	copy constructor, this=dA

	Sparsesym (Integer nr)
	initialize to zero-matrix of size nr*nr

	Sparsesym (Integer nr, Integer nz, const Integer ini, const Integer inj, const Real *va)
	initialize to size nr*nr and nz nonzeros so that this(ini[i],inj[i])=val[i] for i=0,..,nz-1; specify only one of (i,j) and (j,i), multiple elements are summed up.

	Sparsesym (Integer nr, Integer nz, const Indexmatrix &ini, const Indexmatrix &inj, const Matrix &va)
	initialize to size nr*nr and nz nonzeros so that this(ini(i),inj(i))=val[i] for i=0,..,nz-1; specify only one of (i,j) and (j,i), multiple elements are summed up.

void	set_init (bool)
	after external initialization, call matrix.set_init(true) (not needed if CONICBUNDLE_DEBUG is undefined)

bool	get_init () const
	returns true if the matrix has been declared initialized (not needed if CONICBUNDLE_DEBUG is undefined)

Sparsesym &	init (const Sparsesym &, Real d=1.)
	initialize to this=Ad

Sparsesym &	init (const Matrix &, Real d=1.)
	initialize to this=d(A+transpose(A))/2., abs(values)<tol are removed from the support

Sparsesym &	init (const Indexmatrix &, Real d=1.)
	initialize to this=d(A+transpose(A))/2., zeros are removed from the support

Sparsesym &	init (const Symmatrix &, Real d=1.)
	initialize to this=Ad, abs(values)<tol are removed from the support

Sparsesym &	init (const Sparsemat &, Real d=1.)
	initialize to this=d(A+transpose(A))/2.

Sparsesym &	init (Integer nr)
	initialize to zero-matrix of size nr*nr

Sparsesym &	init (Integer nr, Integer nz, const Integer ini, const Integer inj, const Real *va)
	initialize to size nr*nr and nz nonzeros so that this(ini[i],inj[i])=val[i] for i=0,..,nz-1; specify only one of (i,j) and (j,i), multiple elements are summed up.

Sparsesym &	init (Integer nr, Integer nz, const Indexmatrix &ini, const Indexmatrix &inj, const Matrix &va)
	initialize to size nr*nr and nz nonzeros so that this(ini(i),inj(i))=val[i] for i=0,..,nz-1; specify only one of (i,j) and (j,i), multiple elements are summed up.

Sparsesym &	init_support (const Sparsesym &A, Real d=0.)

void	set_tol (Real t)
	set tolerance for recognizing zero values to t

	Sparsesym (const Matrix &, Real d=1.)
	initialize to this=d(A+transpose(A))/2., abs(values)<tol are removed from the support

	Sparsesym (const Indexmatrix &, Real d=1.)
	initialize to this=d(A+transpose(A))/2., zeros are removed from the support

	Sparsesym (const Symmatrix &, Real d=1.)
	initialize to this=Ad, abs(values)<tol are removed from the support

	Sparsesym (const Sparsemat &, Real d=1.)
	initialize to this=d(A+transpose(A))/2.

void	dim (Integer &r, Integer &c) const
	returns the number of rows in _nr and the number of columns in _nc

Integer	dim () const
	returns the dimension rows * columns when the matrix is regarded as a vector

Integer	rowdim () const
	returns the row dimension

Integer	coldim () const
	returns the column dimension

Integer	nonzeros () const
	returns the number of nonzeros in the lower triangle (including diagonal)

Mtype	get_mtype () const
	returns the type of the matrix, MTmatrix

Real	operator() (Integer i, Integer j) const
	returns value of element (i,j) of the matrix (rowindex i, columnindex j)

Real	operator() (Integer i) const
	returns value of element (i) of the matrix if regarded as vector of stacked columns [element (irowdim, i/rowdim)]

Real	operator[] (Integer i) const
	returns value of element (i) of the matrix if regarded as vector of stacked columns [element (irowdim, i/rowdim)]

const Indexmatrix &	get_colinfo () const
	returns information on nozero diagonal/columns, k by 4, listing: index (<0 for diagonal), # nonzeros, first index in colindex/colval, index in suppport submatrix

const Indexmatrix &	get_colindex () const
	returns the index vector of the column representation holding the row index for each element

const Matrix &	get_colval () const
	returns the value vector of the column representation holding the value for each element

const Indexmatrix &	get_suppind () const
	returns the index vector of the column representation holding the row index w.r.t. the principal support submatrix for each element

const Indexmatrix &	get_suppcol () const
	returns the vector listing in ascending order the original column indices of the principal support submatrix

void	get_edge_rep (Indexmatrix &I, Indexmatrix &J, Matrix &val) const
	stores the nz nonzero values of the lower triangle of *this in I,J,val so that this(I(i),J(i))=val(i) for i=0,...,nz-1 and dim(I)=dim(J)=dim(val)=nz (ordered as in row representation)

int	contains_support (const Sparsesym &A) const
	returns 1 if A is of the same dimension and the support of A is contained in the support of *this, 0 otherwise

int	check_support (Integer i, Integer j) const
	returns 0 if (i,j) is not in the support, 1 otherwise

Sparsesym &	xeya (const Sparsesym &A, Real d=1.)
	sets this=dA and returns *this

Sparsesym &	xeya (const Matrix &A, Real d=1.)
	sets and returns this=d(A+transpose(A))/2. where abs(values)<tol are removed from the support

Sparsesym &	xeya (const Indexmatrix &A, Real d=1.)
	sets and returns this=d(A+transpose(A))/2. where zeros are removed from the support

Sparsesym &	support_xbpeya (const Sparsesym &y, Real alpha=1., Real beta=0.)
	returns this= alphay+beta(this) restricted to the curent support of this; if beta==0, then this is initialized to 0 on its support first

Sparsesym &	operator= (const Sparsesym &A)

Sparsesym &	operator+= (const Sparsesym &v)

Sparsesym &	operator-= (const Sparsesym &v)

Sparsesym	operator- () const

Sparsesym &	*operator=** (Real d)

Sparsesym &	operator/= (Real d)
	ATTENTION: d is NOT checked for 0.

Sparsesym &	operator= (const Matrix &A)
	sets this=(A+transpose(A))/2. removing abs(values)<tol; returns this

Sparsesym &	operator= (const Indexmatrix &A)
	sets this=(A+transpose(A))/2. removing zeros; returns this

Sparsesym &	transpose ()
	transposes itself (at almost no cost)

Sparsesym &	xeya (const Symmatrix &A, Real d=1.)
	sets and returns this=Ad where abs(values)<tol are removed from the support

Sparsesym &	xeya (const Sparsemat &A, Real d=1.)
	sets and returns this=d.(A+transpose(A))/2.

Sparsesym &	operator= (const Symmatrix &A)
	sets and returns *this=A where abs(values)<tol are removed from the support

Symmatrix	operator+ (const Symmatrix &A) const

Symmatrix	operator- (const Symmatrix &A) const

Sparsesym &	operator= (const Sparsemat &A)
	sets and returns *this=(A+transpose(A))/2.

Sparsemat	sparsemult (const Matrix &A) const
	compute (this)A and return the result in a Sparsemat

void	display (std::ostream &out, int precision=0, int width=0, int screenwidth=0) const
	displays a matrix in a pretty way for bounded screen widths; for variables of value zero default values are used. More...

Protected Attributes
CH_Matrix_Classes::Matrix	gramblock
	the gram matrix part is gramblock*transpose(grampblock)

Additional Inherited Members
Protected Member Functions inherited from CH_Matrix_Classes::Memarrayuser
	Memarrayuser ()
	if memarray is NULL, then a new Memarray is generated. In any case the number of users of the Memarray is incremented

virtual	~Memarrayuser ()
	the number of users is decremented and the Memarray memory manager is destructed, if the number is zero.

Static Protected Attributes inherited from CH_Matrix_Classes::Memarrayuser
static Memarray *	memarray
	pointer to common memory manager for all Memarrayusers, instantiated in memarray.cxx

Detailed Description

represents an PSCPrimal as the sum 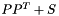$PP^T+S$ of a Gram matrix and a sparse symmetric matrix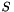 $S$

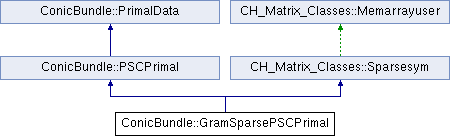
GramSparsePSCPrimal is pubically derived from PSCPrimal and CH_Matrix_Classes::Sparseym, so it may be used directly like a sparse symmetric matrix, but this does then not include or involve the Gram matrix part!

Member Function Documentation

◆ aggregate_Gram_matrix()

int ConicBundle::GramSparsePSCPrimal::aggregate_Gram_matrix	(	const CH_Matrix_Classes::Matrix &	P,
		double	factor = `1.`
	)

inlinevirtual

add factor*P*P^T to this, collecting all available information only in the sparse part, even the own Gram part.

This operation more or less converts this to a SparsePSCPrimal. The point is that this routine is typically only called by PSCModel when aggregating the information in a single aggregate matrix over several steps and it is pointless to try to keep any gram information in this case.

Implements ConicBundle::PSCPrimal.

References CH_Matrix_Classes::Matrix::dim(), CH_Matrix_Classes::Matrix::init(), and CH_Matrix_Classes::support_rankadd().

◆ aggregate_primal_data()

int ConicBundle::GramSparsePSCPrimal::aggregate_primal_data	(	const PrimalData &	it,
		double	factor = `1.`
	)

inlinevirtual

if it is a GramSparsePSCPrimal or SparseSDPRimal, add factor*it to this on only the support of this sparsematrix

Even if it is a GramSparsePSCPrimal and it has a nontirival Gram matrix part, this part is only added to the sparse part of this on the support of the sparse part of this. No attempt is made to enlarge the Gram part.

Implements ConicBundle::PSCPrimal.

References CH_Matrix_Classes::Matrix::dim(), gramblock, and CH_Matrix_Classes::support_rankadd().

The documentation for this class was generated from the following file:

PSCPrimal.hxx

Public Member Functions

Protected Attributes

Additional Inherited Members

Detailed Description

Member Function Documentation

◆ aggregate_Gram_matrix()

◆ aggregate_primal_data()