implements a general purpose dense symmetric PSCPrimal based on CH_Matrix_Classes::Symmatrix More...
#include <PSCPrimal.hxx>
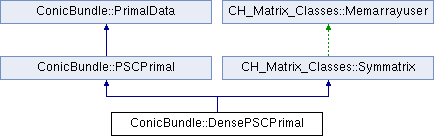
Inheritance diagram for ConicBundle::DensePSCPrimal:
Public Member Functions | |
| DensePSCPrimal () | |
| initialize to a symmetric matrix of size 0 | |
| DensePSCPrimal (const DensePSCPrimal &symmat, double factor=1.) | |
| copy constructor | |
| DensePSCPrimal (const CH_Matrix_Classes::Symmatrix &symmat, double factor=1.) | |
| copy constructor from a CH_Matrix_Classes::Symmatrix | |
| DensePSCPrimal (CH_Matrix_Classes::Integer n) | |
| direct size initialization to a zero matrix | |
| const DensePSCPrimal & | operator= (const CH_Matrix_Classes::Symmatrix &symmat) |
| assigns a symmetric matrix | |
| virtual PrimalData * | clone_primal_data () const |
| returns a newly generated identical Object, see PrimalData::clone_primal_data() | |
| virtual int | assign_Gram_matrix (const CH_Matrix_Classes::Matrix &P) |
| assign P*P^T to this | |
| virtual int | aggregate_primal_data (const PrimalData &it, double factor=1.) |
| add factor*it to this (it must also be a DensePSCPrimal) | |
| virtual int | aggregate_Gram_matrix (const CH_Matrix_Classes::Matrix &P, double factor=1.) |
| add factor*P*P^T to this | |
| virtual int | scale_primal_data (double factor) |
| multiply/scale *this with a nonnegative factor | |
| virtual int | primal_ip (CH_Matrix_Classes::Real &value, const SparseCoeffmatMatrix &A, CH_Matrix_Classes::Integer column) const |
| if compatible evaluate value=ip(*this,A.column[i]) | |
 Public Member Functions inherited from CH_Matrix_Classes::Symmatrix Public Member Functions inherited from CH_Matrix_Classes::Symmatrix | |
| Symmatrix () | |
| empty matrix | |
| Symmatrix (const Symmatrix &A, double d=1.) | |
| copy constructor, *this=d*A | |
| Symmatrix (Integer nr) | |
| generate a matrix of size nr x nr but WITHOUT initializing the memory More... | |
| Symmatrix (Integer nr, Real d) | |
| generate a matrix of size nr x nr initializing all elements to the value d | |
| Symmatrix (Integer nr, const Real *dp) | |
| generate a matrix of size nr x nr initializing the elements from the (one dimensional) array dp, which must have the elements arranged consecutively in internal order | |
| ~Symmatrix () | |
| void | set_init (bool) |
| after external initialization, call matrix.set_init(true) (not needed if CONICBUNDLE_DEBUG is undefined) | |
| bool | get_init () const |
| returns true if the matrix has been declared initialized (not needed if CONICBUNDLE_DEBUG is undefined) | |
| Symmatrix & | init (const Symmatrix &A, double d=1.) |
| initialize to *this=A*d | |
| Symmatrix & | init (const Matrix &A, double d=1.) |
| initialize to this=d(A+transpose(A))/2. | |
| Symmatrix & | init (const Indexmatrix &A, double d=1.) |
| initialize to this=d(A+transpose(A))/2. | |
| Symmatrix & | init (const Sparsesym &A, Real d=1.) |
| initialize to *this=A*d | |
| Symmatrix & | init (Integer nr, Real d) |
| intialize *this to a matrix of size nr x nr initializing all elements to the value d | |
| Symmatrix & | init (Integer nr, const Real *dp) |
| generate a matrix of size nr x nc initializing the elements from the (one dimensional) array dp which must have the elements arranged consecutively in internal order | |
| void | newsize (Integer n) |
| resize the matrix to nr x nr elements but WITHOUT initializing the memory More... | |
| Symmatrix (const Matrix &, double d=1.) | |
| (this)=d(A+transpose(A))/2. | |
| Symmatrix (const Indexmatrix &, double d=1.) | |
| (this)=d(A+transpose(A))/2. | |
| Symmatrix (const Sparsesym &A, Real d=1.) | |
| (*this)=d*A | |
| void | dim (Integer &_nr, Integer &_nc) const |
| returns the number of rows in _nr and _nc | |
| Integer | dim () const |
| returns the dimension rows * columns when the matrix is regarded as a vector | |
| Integer | rowdim () const |
| returns the row dimension | |
| Integer | coldim () const |
| returns the column dimension | |
| Mtype | get_mtype () const |
| returns the type of the matrix, MTsymmetric | |
| Real & | operator() (Integer i, Integer j) |
| returns reference to element (i,j) of the matrix (rowindex i, columnindex j) | |
| Real & | operator() (Integer i) |
| returns reference to element (i) of the matrix if regarded as vector of stacked columns [element (irowdim, i/rowdim)] | |
| Real | operator() (Integer i, Integer j) const |
| returns value of element (i,j) of the matrix (rowindex i, columnindex j) | |
| Real | operator() (Integer i) const |
| returns value of element (i) of the matrix if regarded as vector of stacked columns [element (irowdim, i/rowdim)] | |
| Matrix | col (Integer i) const |
| returns column i copied to a new Matrix | |
| Matrix | row (Integer i) const |
| returns row i copied to a new Matrix | |
| Matrix | cols (const Indexmatrix &vec) const |
| returns a matrix of size this->rowdim() x vec.dim(), with column i a copy of column vec(i) of *this | |
| Matrix | rows (const Indexmatrix &vec) const |
| returns a matrix of size vec.dim() x this->coldim(), with row i a copy of row vec(i) of *this | |
| Symmatrix & | swapij (Integer i, Integer j) |
| swaps rows (and columns) i and j | |
| Symmatrix & | pivot_permute (const Indexmatrix &piv, bool inverse=false) |
| for i=0 to rowdim row (and column) i of this matrix is swapped with row piv(j); for inverse=true the inverse permutation is generated | |
| Symmatrix & | principal_submatrix (const Indexmatrix &ind, Symmatrix &S) const |
| returns S and in S the principal submatrix indexed by ind (multiple indices are allowed) | |
| Symmatrix | principal_submatrix (const Indexmatrix &ind) const |
| returns the principal submatrix indexed by ind (multiple indices are allowed) | |
| Symmatrix & | delete_principal_submatrix (const Indexmatrix &ind, bool sorted_increasingly=false) |
| returns this afte deleting the principal submatrix indexed by ind (no repetitions!); | |
| Symmatrix & | enlarge_below (Integer addn) |
| increases the order of the matrix by appending storage for further addn rows and columns (marked as not initiliazed if addn>0, no changes if addn<=0) | |
| Symmatrix & | enlarge_below (Integer addn, Real d) |
| increases the order of the matrix by appending storage for further addn rows and columns initialized to d (no changes if addn<=0); | |
| Real * | get_store () |
| returns the current address of the internal value array; use cautiously, do not use delete! | |
| const Real * | get_store () const |
| returns the current address of the internal value array; use cautiously! | |
| Symmatrix & | xeya (const Symmatrix &A, Real d=1.) |
| sets *this=d*A and returns *this | |
| Symmatrix & | xpeya (const Symmatrix &A, Real d=1.) |
| sets *this+=d*A and returns *this | |
| Symmatrix & | operator= (const Symmatrix &A) |
| Symmatrix & | operator+= (const Symmatrix &A) |
| Symmatrix & | operator-= (const Symmatrix &A) |
| Symmatrix & | operator%= (const Symmatrix &A) |
| ATTENTION: this is redefined as the Hadamard product, (*this)(i,j)=(*this)(i,j)*A(i,j) for all i<=j. | |
| Symmatrix | operator- () const |
| Symmatrix & | operator*= (Real d) |
| Symmatrix & | operator/= (Real d) |
| ATTENTION: d is NOT checked for 0. | |
| Symmatrix & | operator+= (Real d) |
| sets (*this)(i,j)+=d for all i<=j | |
| Symmatrix & | operator-= (Real d) |
| sets (*this)(i,j)-=d for all i<=j | |
| Symmatrix & | transpose () |
| transposes itself (at almost no cost) | |
| Symmatrix & | xeya (const Matrix &A, Real d=1.) |
| sets this=d(A+transpose(A))/2. and returns *this | |
| Symmatrix & | xpeya (const Matrix &A, Real d=1.) |
| sets this+=d(A+transpose(A))/2. and returns *this | |
| Symmatrix & | xeya (const Indexmatrix &A, Real d=1.) |
| sets this=d(A+transpose(A))/2. and returns *this | |
| Symmatrix & | xpeya (const Indexmatrix &A, Real d=1.) |
| sets this+=d(A+transpose(A))/2. and returns *this | |
| Symmatrix & | xeya (const Sparsesym &A, Real d=1.) |
| sets *this=d*A and returns *this | |
| Symmatrix & | xpeya (const Sparsesym &A, Real d=1.) |
| sets *this+=d*A and returns *this | |
| Symmatrix & | xetriu_yza (const Matrix &A, const Matrix &B, Real d=1.) |
| sets *this(i,j), i<=j to the upper triangle of the matrix product d*transpose(A)*B | |
| Symmatrix & | xpetriu_yza (const Matrix &A, const Matrix &B, Real d=1.) |
| adds to *this(i,j), i<=j the upper triangle of the matrix product d*transpose(A)*B | |
| Symmatrix & | xetriu_yza (const Sparsemat &A, const Matrix &B, Real d=1.) |
| sets *this(i,j), i<=j to the upper triangle of the matrix product d*transpose(A)*B | |
| Symmatrix & | xpetriu_yza (const Sparsemat &A, const Matrix &B, Real d=1.) |
| adds to *this(i,j), i<=j the upper triangle of the matrix product d*transpose(A)*B | |
| Symmatrix & | operator= (const Sparsesym &A) |
| Symmatrix & | operator+= (const Sparsesym &A) |
| Symmatrix & | operator-= (const Sparsesym &A) |
| Symmatrix & | shift_diag (Real s) |
| shifts the diagonal by s, i.e., (*this)(i,i)+=s for all i | |
| int | LDLfactor (Real tol=1e-10) |
| computes LDLfactorization (implemented only for positive definite matrices so far, no pivoting), (*this) is overwritten by the factorization; returns 1 if diagonal elements go below tol | |
| int | LDLsolve (Matrix &x) const |
| computes, after LDLfactor was executed succesfully, the solution to (*old_this)x=rhs; rhs is overwritten by the solution; always returns 0; NOTE: there is NO check against division by zero | |
| int | LDLinverse (Symmatrix &S) const |
| computes, after LDLfactor was executed succesfully, the inverse to (*old_this) and stores it in S (numerically not too wise); always returns 0; NOTE: there is NO check against division by zero | |
| int | Chol_factor (Real tol=1e-10) |
| computes the Cholesky factorization, for positive definite matrices only, (*this) is overwritten by the factorization; there is no pivoting; returns 1 if diagonal elements go below tol | |
| int | Chol_solve (Matrix &x) const |
| computes, after Chol_factor was executed succesfully, the solution to (*old_this)x=rhs; rhs is overwritten by the solution; always returns 0; NOTE: there is NO check against division by zero | |
| int | Chol_inverse (Symmatrix &S) const |
| computes, after Chol_factor was executed succesfully, the inverse to (*old_this) and stores it in S (numerically not too wise); always returns 0; NOTE: there is NO check against division by zero | |
| int | Chol_Lsolve (Matrix &rhs) const |
| computes, after Chol_factor into LL^T was executed succesfully, the solution to Lx=rhs; rhs is overwritten by the solution; always returns 0; NOTE: there is NO check against division by zero | |
| int | Chol_Ltsolve (Matrix &rhs) const |
| computes, after Chol_factor into LL^T was executed succesfully, the solution to L^Tx=rhs; rhs is overwritten by the solution; always returns 0; NOTE: there is NO check against division by zero | |
| int | Chol_scaleLi (Symmatrix &S) const |
| computes, after Chol_factor into LL^T was executed succesfully, L^{-1}SL^{-T} overwriting S | |
| int | Chol_scaleLt (Symmatrix &S) const |
| computes, after Chol_factor into LL^T was executed succesfully, L^TSL overwriting S | |
| int | Chol_Lmult (Matrix &rhs) const |
| computes, after Chol_factor into LL^T was executed succesfully, L*rhs, overwriting rhs by the result; always returns 0; | |
| int | Chol_Ltmult (Matrix &rhs) const |
| computes, after Chol_factor into LL^T was executed succesfully, L^Trhs, overwriting rhs by the result; always returns 0; | |
| int | Chol_factor (Indexmatrix &piv, Real tol=1e-10) |
| computes the Cholesky factorization with pivoting, for positive semidefinite matrices only, (*this) is overwritten by the factorization; on termination piv.dim() is the number of positive pivots>=tol; returns 1 if negative diagonal element is encountered during computations, 0 otherwise. | |
| int | Chol_solve (Matrix &x, const Indexmatrix &piv) const |
| computes, after Chol_factor(Indexmatrix&,Real) with pivoting was executed succesfully, the solution to (*old_this)*x=rhs(piv); rhs is overwritten by the solution arranged in original unpermuted order; always returns 0; NOTE: there is NO check against division by zero | |
| int | Chol_inverse (Symmatrix &S, const Indexmatrix &piv) const |
| computes, after Chol_factor(Indexmatrix&,Real) with pivoting was executed succesfully, the inverse to (*old_this) and stores it in S (the pivoting permutation is undone in S); NOTE: there is NO check against division by zero | |
| int | Aasen_factor (Indexmatrix &piv) |
| computes Aasen factorization LTL^T with pivoting, where L is unit lower triangular with first colum e_1 and T is tridiagonal; (*this) is overwritten by the factorization, with column i of L being stored in column i-1 of (*this); always returns 0; | |
| int | Aasen_Lsolve (Matrix &x) const |
| computes, after Aasen_factor into LTL^T was executed, the solution to Lx=rhs; rhs is overwritten by the solution; always returns 0; | |
| int | Aasen_Ltsolve (Matrix &x) const |
| computes, after Aasen_factor into LTL^T was executed, the solution to L^Tx=rhs; rhs is overwritten by the solution; always returns 0; | |
| int | Aasen_tridiagsolve (Matrix &x) const |
| computes, after Aasen_factor into LTL^T was executed, the solution to Tx=rhs; rhs is overwritten by the solution;if the solution fails due to division by zero (=system not solvable) the return value is -(rowindex+1) where this occured in the backsolve | |
| int | Aasen_solve (Matrix &x, const Indexmatrix &piv) const |
| computes, after Aasen_factor into LTL^T was executed, the solution to (*old_this)x=rhs; rhs is overwritten by the solution; if the solution fails due to division by zero (=system not solvable) the return value is -(rowindex+1) where this occured in the backsolve | |
| Integer | eig (Matrix &P, Matrix &d, bool sort_non_decreasingly=true) const |
| computes an eigenvalue decomposition P*Diag(d)*tranpose(P)=(*this) by symmetric QR; returns 0 on success, | |
| void | display (std::ostream &out, int precision=0, int width=0, int screenwidth=0) const |
| displays a matrix in a pretty way for bounded screen widths; for variables of value zero default values are used. More... | |
| void | mfile_output (std::ostream &out, int precision=16, int width=0) const |
| outputs a matrix A in the format "[ A(0,1) ... A(0,nc-1)\n ... A(nr-1,nc-1)];\n" so that it can be read e.g. by octave as an m-file More... | |
| void | init_svec (Integer nr, const Real *dp, Integer incr=1, Real d=1.) |
| void | store_svec (Real *dp, Integer incr=1, Real d=1.) const |
Additional Inherited Members | |
 Protected Member Functions inherited from CH_Matrix_Classes::Memarrayuser Protected Member Functions inherited from CH_Matrix_Classes::Memarrayuser | |
| Memarrayuser () | |
| if memarray is NULL, then a new Memarray is generated. In any case the number of users of the Memarray is incremented | |
| virtual | ~Memarrayuser () |
| the number of users is decremented and the Memarray memory manager is destructed, if the number is zero. | |
 Static Protected Attributes inherited from CH_Matrix_Classes::Memarrayuser Static Protected Attributes inherited from CH_Matrix_Classes::Memarrayuser | |
| static Memarray * | memarray |
| pointer to common memory manager for all Memarrayusers, instantiated in memarray.cxx | |
Detailed Description
implements a general purpose dense symmetric PSCPrimal based on CH_Matrix_Classes::Symmatrix
DensePSCPrimal is pubically derived from PSCPrimal and CH_Matrix_Classes::Symmatrix, so it may be used directly like a symmetric matrix
The documentation for this class was generated from the following file:
 1.8.13
1.8.13