Solve 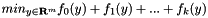 for convex functions f_i, the y-variables may be free, bounded, box constrained, or linearly constrained. The most important steps are the following.
More...
for convex functions f_i, the y-variables may be free, bounded, box constrained, or linearly constrained. The most important steps are the following.
More...
Classes | |
| class | ConicBundle::PrimalMatrix |
| If in Lagrangean relaxation primal solutions are in the form of a real vector or, more generally a matrix, then an approximate primal solution can be generated by supplying primal information of this form for each epsilon subgradient within ConicBundle::MatrixFunctionOracle::evaluate(). More... | |
| class | ConicBundle::MatrixMinorant |
| Minorant interface supporting Matrix classes; simple constructros for subgradients given by column vectors in form of a CH_Matrix_Classes::Matrix or a CH_Matrix_Classes::Sparsemat. More... | |
| class | ConicBundle::ModifiableOracleObject |
| ModifiableOracle provides all oracles with a uniform interface for a modification routine and an on/off switch for internal correctness checks. More... | |
| class | ConicBundle::MatrixFunctionOracle |
| Oracle interface (abstract class). For each of your functions, provide an instance of a derived class. More... | |
| class | ConicBundle::MatrixCBSolver |
| The Full Conic Bundle method solver invoked by ConicBundle::MatrixCBSolver(), it uses a separate cutting model for each function. More... | |
| class | ConicBundle::AffineFunctionTransformation |
| transform a function f(z) to fun_coeff*f(arg_offset+arg_trafo*y)+linear_cost*y+fun_offset (scales the value, substitutes argument z=c+Ay, and adds an affine term b'y+d) More... | |
Detailed Description
Solve 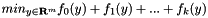 for convex functions f_i, the y-variables may be free, bounded, box constrained, or linearly constrained. The most important steps are the following.
for convex functions f_i, the y-variables may be free, bounded, box constrained, or linearly constrained. The most important steps are the following.
Before starting, note that this interface relies on several classes defined in CH_Matrix_Classes, in particular on CH_Matrix_Classes::Matrix and CH_Matrix_Classes::Indexmatrix. The full functionality of ConicBundle is only available with these classes. If you prefer an interface without having to use these, please use the Interface to ConicBundle for the Language C++. We now give a short overview of the most important steps in using the ConicBundle solver.
Setting up the Problem, the Functions, and the Main Loop
First create a new problem/solver ConicBundle::MatrixCBSolver, let us call it solver for brevity.
Next call ConicBundle::MatrixCBSolver::init_problem() to set the dimension of the design variables/argument space, possibly together with box constraints, starting values and and linear cost terms. In prinicple, further linear constraints could be installed using ConicBundle::MatrixCBSolver::append_constraints() but this should be avoided whenever possible (additional constraints may entail a significant loss in efficiency in the internal quadratic subproblems. Also note that even simple bounds require a lot more work when using general variable metric approaches.
Now set up each of your functions f_i as a ConicBundle::MatrixFunctionOracle (see The Internal Conic Bundle Solver for specialized oracle classes). The solver will call the routine ConicBundle::MatrixFunctionOracle::evaluate(), and via this you have to supply, for a given argument, a function value and an affine ConicBundle::Minorant (you might want to use the constructors provided in MatrixMinorant instead). A Minorant is described by its function value and (epsilon) subgradient (=the gradient if the function is differentiable). In the oracle this function evaluate() is the only function that you definitely have to provide, see the miniature example below.
The function oracles have to be added to the solver using the routine ConicBundle::MatrixCBSolver::add_function(). In adding a function 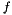 you may (but need not) specify a multiplicative factor
you may (but need not) specify a multiplicative factor 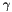 (==1. by default) for
(==1. by default) for 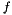 and whether the function serves as an ObjectiveFunction (the solver uses the value
and whether the function serves as an ObjectiveFunction (the solver uses the value 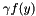 directly), as a ConstantPenaltyFunction (the solver uses the value
directly), as a ConstantPenaltyFunction (the solver uses the value 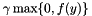 ) or as an AdaptivePenatlyFunction (the solver uses the value
) or as an AdaptivePenatlyFunction (the solver uses the value 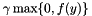 but may further increase
but may further increase 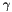 until the value indeed goes to zero). If your function works just on a subset/subspace of the variables, it may be worth to specify the function on its own original space and use a ConicBundle::AffineFunctionTransformation on the argument, so that the solver uses, e.g.
until the value indeed goes to zero). If your function works just on a subset/subspace of the variables, it may be worth to specify the function on its own original space and use a ConicBundle::AffineFunctionTransformation on the argument, so that the solver uses, e.g. 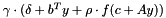 .
.
Once all functions are added, the optimization process can be started. If you know a good starting point (and have not already supplied it in init_problem()) then set it with ConicBundle::MatrixCBSolver::set_new_center_point() now, otherwise the method will pick the zero vector or, in the case of box constraints, the point closest to zero as starting point.
Finally, call ConicBundle::MatrixCBSolver::solve() and retrieve ConicBundle::MatrixCBSolver::termination_code() for getting the reason for termination. Via parameters in solve() you may also tell the solver to return after each descent step or also after a maximum number of null steps. This then only interrupts computations and calling solve() again continues as if there was not break at all.
Retrieving Some Solution Information
Whenever the solver returns form solve() you can retrieve the current objective value by ConicBundle::MatrixCBSolver::get_objval() and the argument leading to this value by ConicBundle::MatrixCBSolver::get_center(). For some screen output, use ConicBundle::MatrixCBSolver::set_out().
Lagrangean Relaxation, Primal Approximations, and Cutting Planes
If you are optimizing the Lagrange multipliers of a Lagrangean relaxation, you might be interested in getting an approximation to your primal optimal solution. This can be done by specifying in each function for each minorant/(epsilon) subgradient the corresponding primal vectors that generate it, see PrimalData (with implementation PrimalMatrix) in ConicBundle::Minorant as a start. Then for each of your functions, you can retrieve the current primal approximation using ConicBundle::MatrixCBSolver::get_approximate_primal().
If you are just relaxing linear constraints on your variables, an elegant alternative is to use an AffineFunctionTransformation as follows. For concreteness, assume you want to minimize ![$f(y)=\max_{x\in\mathcal{X}}[h(x)+(b-Bx)^Ty]$](form_126.png) where
where 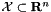 is some compact set for which the inner max is easy to compute for any
is some compact set for which the inner max is easy to compute for any 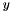 . Now, it might actually be better to implement the function
. Now, it might actually be better to implement the function ![$\bar f(\bar c)=\max_{x\in\mathcal{X}}[h(x)+\bar c^Tx]$](form_128.png) and use it with the AffineFunctionTransformation
and use it with the AffineFunctionTransformation 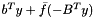 (so
(so 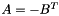 ). Then if
). Then if 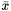 is the maximizer for a given
is the maximizer for a given 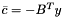 , the corresponding minorant to be returned by the oracle of
, the corresponding minorant to be returned by the oracle of 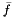 is described by the offset
is described by the offset 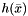 with the corresponding subgradient being just
with the corresponding subgradient being just 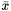 itself. So in this case the primal data is the minorant itself and there is no need to provide it separately. For the case that
itself. So in this case the primal data is the minorant itself and there is no need to provide it separately. For the case that 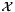 is a box domain, see box oracle with special purpose cutting model for a tuned model. A slightly different possibility is offered by the example implemention of MatrixFunctionOracle (NNCBoxSupportFunction) with an NNCBoxSupportFunction, but this is likely a lot less efficient.
is a box domain, see box oracle with special purpose cutting model for a tuned model. A slightly different possibility is offered by the example implemention of MatrixFunctionOracle (NNCBoxSupportFunction) with an NNCBoxSupportFunction, but this is likely a lot less efficient.
In addition, you might plan to improve your primal relaxation via cutting planes if they are strongly violated by the current primal approximation. This requires introducing new multipliers for the ground set and typically also changes the dimension of your function 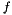 on the fly, unless you are in the situation of
on the fly, unless you are in the situation of 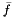 above, where only the AffineFunctionTransformation changes. In any case you will need ConicBundle::MatrixCBSolver::append_variables(). There you have to provide for your function either a corresponding derived implementation of the base class ConicBundle::OracleModification or, in the case of
above, where only the AffineFunctionTransformation changes. In any case you will need ConicBundle::MatrixCBSolver::append_variables(). There you have to provide for your function either a corresponding derived implementation of the base class ConicBundle::OracleModification or, in the case of 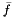 above, just a corresponding ConicBundle::AFTModification for your transformation. In the latter case this is all you need to provide, because
above, just a corresponding ConicBundle::AFTModification for your transformation. In the latter case this is all you need to provide, because 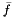 is not changed at all, but in the general case of a general
is not changed at all, but in the general case of a general 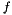 you will also need to implement the oracle's subroutine MatrixFunctionOracle::apply_modification() which will be called by the solver with your modification data so that the function adapts according to this data. In most cases adapting the class ConicBundle::Modification like in ConicBundle::LPGroundsetModification will allow to do all you need with minimal work.
you will also need to implement the oracle's subroutine MatrixFunctionOracle::apply_modification() which will be called by the solver with your modification data so that the function adapts according to this data. In most cases adapting the class ConicBundle::Modification like in ConicBundle::LPGroundsetModification will allow to do all you need with minimal work.
Typically, when changing the dimension, the cutting model of the bundle method is lost. This is no problem in the case of 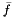 above if the newly added multipliers are zero initially, because then the minorants with transformation can and will be regenerated automatically from the unchanged minorants
above if the newly added multipliers are zero initially, because then the minorants with transformation can and will be regenerated automatically from the unchanged minorants 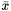 . In the case of general
. In the case of general 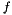 , if you provided primal data with your minorants, you may also know how to extend your minorants on newly appended coordinates. If you know how to do this, then you can provide a ConicBundle::MinorantExtender when the solver calls MatrixFunctionOracle::apply_modification(). The MinorantExtender will be applied to all minorants of the model and if this succeeds the model is not lost. A rich example implementation (with a separate cutting model) of all these features is provided by the PSCAffineFunction implementation of the PSCOracle for solving the duals to primal semidefinite programs with nonempty bounded feasible sets, see abstract positive semidefinite cone oracle and implemention of a PSCOracle (PSCAffineFunction).
, if you provided primal data with your minorants, you may also know how to extend your minorants on newly appended coordinates. If you know how to do this, then you can provide a ConicBundle::MinorantExtender when the solver calls MatrixFunctionOracle::apply_modification(). The MinorantExtender will be applied to all minorants of the model and if this succeeds the model is not lost. A rich example implementation (with a separate cutting model) of all these features is provided by the PSCAffineFunction implementation of the PSCOracle for solving the duals to primal semidefinite programs with nonempty bounded feasible sets, see abstract positive semidefinite cone oracle and implemention of a PSCOracle (PSCAffineFunction).
If you want to get rid of primal constraints/dual variables, have a look at ConicBundle::MatrixCBSolver::set_active_bounds_fixing(), ConicBundle::MatrixCBSolver::get_fixed_active_bounds(), maybe also at ConicBundle::MatrixCBSolver::get_approximate_slacks() and then use ConicBundle::MatrixCBSolver::delete_variables(). This may again need to be accompanied by OracleModifcation implementations and corresponding actions in your oracle.
 1.8.13
1.8.13