Minorant interface supporting Matrix classes; simple constructros for subgradients given by column vectors in form of a CH_Matrix_Classes::Matrix or a CH_Matrix_Classes::Sparsemat. More...
#include <MatrixCBSolver.hxx>
Inheritance diagram for ConicBundle::MatrixMinorant:
Public Member Functions | |
| MatrixMinorant (CH_Matrix_Classes::Real offset, const CH_Matrix_Classes::Matrix &subg, PrimalData *primal=0, bool offset_at_origin=false) | |
| initializaton by a Matrix column vector; if offset_at_origin==true, the offset gives the value at the origin (in contrast to the value at the current evaluation point) | |
| MatrixMinorant (CH_Matrix_Classes::Real offset, const CH_Matrix_Classes::Sparsemat &subg, PrimalData *primal=0, bool offset_at_origin=false) | |
| initializaton by a Sparsemat column vector; if offset_at_origin==true, the offset gives the value at the origin (in contrast to the value at the current evaluation point) | |
| MatrixMinorant (const Minorant *mnrt, CH_Matrix_Classes::Real factor=1., bool with_primal=true) | |
| generates a MatrixMinorat copy of a Minorant scaled by factor (deault =1.) and optionally without cloning the primal (if it exists) | |
| Minorant * | clone_minorant (double factor=1., bool with_primal=true) const |
| produces a clone of itself | |
 Public Member Functions inherited from ConicBundle::Minorant | |
| Minorant (double offset, const DVector &subg, PrimalData *primal=0, bool offset_at_origin=false) | |
| Minorant constructor for a dense subgradient specified via a DVector. More... | |
| Minorant (double offset, const DVector &subg_val, const IVector &subg_ind, PrimalData *primal=0, bool offset_at_origin=false) | |
| Minorant constructor for a sparse subgradient where the nonzero values are specified by DVector and the corresponding indices by an IVector. More... | |
| Minorant (bool offset_at_origin=true, double offset=0., int n_elementes=0, const double *coeffs=0, const int *indices=0, double scale_val=1., PrimalData *primal=0) | |
| default initializes a zero minorant, see full explanation otherwise; NOTE: if the offset supplied by the minorant refers to the evaluation point (i.e., if it is the function value at the point of evaluation), set offset_at_origin = false ! More... | |
| Minorant (const Minorant *mnrt, double factor=1., bool with_primal=false) | |
| they main purpose of this constructor is to allow easy cloning for derived classes | |
| virtual double | offset () const |
| returns the current offset value | |
| virtual int | add_offset (double value) |
| adds this value to the current offset value | |
| virtual bool & | offset_gives_value_at_origin () |
| allows to specify/modify whether the offset refers to origin or to the point of evaluation at which this minorant was supplied | |
| virtual bool | offset_gives_value_at_origin () const |
| true if the offset refers to origin and false, if the offset refers to the value of the minorant in the point of the oracle evaluation at which this minorant was supplied | |
| virtual double | coeff (int i) |
| returns the value of the coefficient in coordinate i | |
| virtual int | add_coeff (int i, double value) |
| adds the value to the coefficient in coordinate i | |
| virtual int | add_coeffs (int n_elements, const double *values, double factor=1., int start_pos=0) |
| adds the n values (possibly multiplied by factor) to consecutive coefficients starting at start_pos (by default 0); this always converts the minroant into a dense vector first and adds then | |
| virtual int | add_coeffs (int n_elements, const double *values, const int *indices, double factor=1.) |
| adds the n values (possibly multiplied by factor) to the coefficients indicated by indices (if zero, this calls the other add_coeffs for the consecutive version) | |
| virtual int | sparsify (double tol=CB_minorant_zero_tolerance, double sparsity_ratio=CB_minorant_sparsity_ratio) |
| converts to sparse format with zeros of absolut value at most tol*(fabs(offset)+1) if the given ratio of elements is zero in relation to the maximum nonzero index | |
| virtual int | nonzeros () |
| returns the number of nonzero coefficients | |
| virtual int | get_coeffs (int &n_elements, const double *&coeffs, const int *&indices) const |
| returns the list of all nonzero coefficients by returning pointers to the arrays and their common length n_elements More... | |
| virtual double * | get_dense_coeff_store (int n_elements) |
| If the returned pointer is not NULL it gives direct access to the array of current coefficient values with indices 0 up to n_elements-1;. More... | |
| virtual int | reassign_coeffs (int n_elements, const int *map_to_old_coeffs) |
| resorts (and deletes) coefficients so that afterwards it has n_elements and the new coeff(i) has the previous value of coeff(map_to_old_coeff(i)) | |
| virtual void | set_primal (PrimalData *) |
| if the minorant is generated by PrimalData and this should be aggregated along, insert a heap object of it here (see PrimalData) | |
| virtual PrimalData * | get_primal () |
| returns NULL if there is no primal data and otherwise a pointer to it | |
| virtual const PrimalData * | get_primal () const |
| returns NULL if there is no primal data and otherwise a pointer to it (const version) | |
| virtual int | aggregate (const Minorant &minorant, double factor=1.) |
| adds factor*minorant to this and does this also for the primal if it is availabe | |
| virtual int | number_aggregated () const |
| returns the number of minorants aggregated in this one, value 1 thus means not aggregated | |
| virtual int | scale_minorant (double scale_val) |
| mutliply offset and coefficients (and PrimalData, if given) by scale_val | |
| virtual double | norm_squared () const |
| return the squared Euclidean norm | |
Additional Inherited Members | |
| Protected Member Functions inherited from ConicBundle::Minorant | |
| Minorant (const Minorant &) | |
| forbidden, blocked deliberately | |
| Minorant & | operator= (const Minorant &) |
| forbidden, blocked deliberately | |
| Protected Attributes inherited from ConicBundle::Minorant | |
| MinorantData * | data |
| implementation details are hidden on purpose | |
Detailed Description
Minorant interface supporting Matrix classes; simple constructros for subgradients given by column vectors in form of a CH_Matrix_Classes::Matrix or a CH_Matrix_Classes::Sparsemat.
Suppose in the evaluation of your oracle at the current point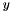 
you determine the subgradient 
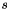for the subgradient inequality
![\[ f(z)\ge f(y)+\langle s,z-y\rangle\quad\forall z\in\mathbf{R}^m, \]](form_117.png)
then use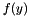 
for offset and 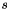for subg in the constructors and keep the default value offset_at_origin == false.
If, on the other hand, your oracle implements a support function for some compact set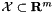 
like
![\[ f(y) = \max_{x\in\mathcal{X}} x^\top y\]](form_120.png)
then it is actually more efficient to return 0 for offset, a maximizing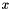 
in @ subg and to put offset_at_origin = true.
The documentation for this class was generated from the following file:
