Solve 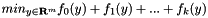 for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here. Internal details are sketched in Internal implementation of the "C" interface.
More...
for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here. Internal details are sketched in Internal implementation of the "C" interface.
More...
Typedefs | |
| typedef struct CB_CSolver * | cb_problemp |
| pointer to a ConicBundle problem | |
| typedef int(* | cb_functionp) (void *function_key, double *arg, double relprec, int max_subg, double *objective_value, int *n_subgrads, double *subg_values, double *subgradients, double *primal) |
| function oracle; describe your function as a function of this type to pass it to the solver More... | |
| typedef int(* | cb_subgextp) (void *function_key, double *generating_primal, int n_indices, int *variable_indices, double *new_subgradient_values) |
| This routine is not needed unless variabls (constraints in Lagrangean relaxation) are added on the fly. More... | |
Functions | |
| cb_problemp | cb_construct_problem (int no_bundle) |
| Creates a a new problem object and returns a pointer to it. More... | |
| int | cb_destruct_problem (cb_problemp *p) |
| Destructs and frees the problem object. More... | |
| void | cb_clear (cb_problemp p) |
| Clears all data structures and problem information but keeps ouptut settings and algorithmic parameter settings. More... | |
| void | cb_set_defaults (cb_problemp p) |
| Sets default values for algorithmic parameters that are not function specific (e.g., relative precision, weight and weight bounds for the augmentedproblem, etc.) More... | |
| int | cb_init_problem (cb_problemp p, int m, double *lowerb, double *upperb) |
| Initializes the problem by setting the design space (the dimension and possible box constraints of the variables) More... | |
| int | cb_add_function (cb_problemp p, void *function_key, cb_functionp f, cb_subgextp se, int primaldim) |
| Adds the function, the sum of which should be minimized, to the problem description. More... | |
| int | cb_set_lower_bound (cb_problemp p, int i, double lower_bound) |
| set lower bound for variable i, use cb_get_minus_infinity() for unbounded from below. More... | |
| int | cb_set_upper_bound (cb_problemp p, int i, double upper_bound) |
| set upper bound for variable i, use cb_get_plus_infinity() for unbounded above. More... | |
| int | cb_append_variables (cb_problemp p, int n_append, double *lower_bound, double *upper_bound) |
| Append new variables (always in last postions in this order). More... | |
| int | cb_delete_variables (cb_problemp p, int n_del, int *delete_indices, int *map_to_old) |
| Deletes variables corresponding to the specified indices. More... | |
| int | cb_reassign_variables (cb_problemp p, int n_assign, int *assign_new_from_old) |
| Reassigns variables to new index positions by mapping to position i the variable that previously had index assign_new_from_old[i]. More... | |
| int | cb_solve (cb_problemp p, int maxsteps, int stop_at_descent_steps) |
| solves or does a prescribed number of More... | |
| int | cb_termination_code (cb_problemp p) |
| Returns the termination code of the bundle algorithm for the latest descent step. More... | |
| int | cb_print_termination_code (cb_problemp p) |
| Outputs a text version of termination code, see cb_termination_code(). More... | |
| double | cb_get_objval (cb_problemp p) |
| Returns the objective value resulting from last descent step (initially undefined). More... | |
| int | cb_get_center (cb_problemp p, double *center) |
| Returns the next center point that was produced by the last call to cb_do_descent_step (in some problem modification routines the center point may be updated immediately, in others the center point will be corrected automatically directly before starting the next descent step and its values may be infeasible till then). More... | |
| double | cb_get_sgnorm (cb_problemp p) |
| Returns Euclidean norm of the latest aggregate subgradient. More... | |
| int | cb_get_subgradient (cb_problemp p, double *subgradient) |
| Returns the latest aggregate subgradient. More... | |
| double | cb_get_candidate_value (cb_problemp p) |
| Returns the objective value computed in the last step of do_descent_step(), independent of whether this was a descent step or a null step (initially undefined). More... | |
| int | cb_get_candidate (cb_problemp p, double *candidate) |
| Returns the last point, the "candidate", at which the function was evaluated in cb_do_descent_step(). More... | |
| int | cb_set_term_relprec (cb_problemp p, double term_relprec) |
| Sets the relative precision requirements for successful termination (default 1e-5). More... | |
| int | cb_set_new_center_point (cb_problemp p, double *center) |
| Set the starting point/center that will be used in the next call to cb_do_descent_step(). Each call to this routine causes an immediate evaluation of all oracles. More... | |
| int | cb_get_function_status (cb_problemp p, void *function_key) |
| Returns the return value of the latest evaluation call to the function with this function_key. More... | |
| int | cb_get_approximate_slacks (cb_problemp p, double *slacks) |
| Returns the multipliers for the bound constraints on the design variables; in Lagrangean relaxation they may be interpreted as primal slacks for inequality constraints. More... | |
| int | cb_get_approximate_primal (cb_problemp p, void *function_key, double *primal) |
| Returns the current approximate primal solution for the function having this function_key. More... | |
| int | cb_get_center_primal (cb_problemp p, void *function_key, double *primal) |
| Returns the best primal solution obtained in the current center point in evaluating the function having this function_key. More... | |
| int | cb_get_candidate_primal (cb_problemp p, void *function_key, double *primal) |
| Returns the best primal solution returned by the last evaluation of the function having this function_key in the point cb_get_candidate(). More... | |
| int | cb_set_max_modelsize (cb_problemp p, void *function_key, int modelsize) |
| Sets the maximum number of subgradients used in forming the cutting model of the function having this function_key. More... | |
| int | cb_set_max_bundlesize (cb_problemp p, void *function_key, int bundlesize) |
| Sets the maximum number of subgradients stored for use in forming the model or determining metric information of the function having this function_key. it must be as least as large as max_modelsize (and is increased to this if not) More... | |
| int | cb_set_max_new_subgradients (cb_problemp p, void *function_key, int max_new_subg) |
| Sets the maximum number of epsilon subgradients that can be returned in one call to the function having this function_key. More... | |
| int | cb_get_bundle_parameters (cb_problemp p, void *function_key, int *max_modelsize, int *max_bundelsize) |
| Retrieves the two bundle parameters specified in the routines cb_set_max_modelsize() and cb_set_max_bundlesize(). for the function having this function_key. More... | |
| int | cb_reinit_function_model (cb_problemp p, void *function_key) |
| Clears cutting model, subgradients and stored function values for the function with this function_key. More... | |
| double | cb_get_last_weight (cb_problemp p) |
| Returns the current weight for the quadratic term in the augmented subproblem (may be interpreted as 1./step_size or 1./trustregion-radius). More... | |
| int | cb_set_next_weight (cb_problemp p, double weight) |
| Sets the weight (>0) to be used in the quadratic term of the next augmented subproblem (may be interpreted as 1./step_size or 1./trustregion-radius). More... | |
| int | cb_set_min_weight (cb_problemp p, double min_weight) |
| Sets a lower bound on the weight for the quadratic term of the augmented subproblem. More... | |
| int | cb_set_max_weight (cb_problemp p, double max_weight) |
| Sets an upper bound on the weight for the quadratic term of the augmented subproblem. More... | |
| int | cb_set_variable_metric (cb_problemp p, int do_variable_metric) |
| Use a variable metric heuristic or switch it off alltogether. (the variable metric heuristic resets the quadratic term to some diagonal or low rank matrix, switching it off resets the proximal term to the identity) More... | |
| int | cb_get_dim (cb_problemp p) |
| Returns the current dimension of the design space/argument or -1 if no dimension is set. | |
| int | cb_get_n_functions (cb_problemp p) |
| Returns the current number of functions in the problem. | |
| double | cb_get_minus_infinity (void) |
| Returns the value "minus infinity", i.e., all bounds <= this value are set to this value and are regarded as minus infinity. | |
| double | cb_get_plus_infinity (void) |
| Returns the value "plus infinity", i.e., all bounds >= this value are set to this value and are regarded as plus infinity. | |
| void | cb_clear_fail_counts (cb_problemp p) |
| clears all fail counts on numerical function oder model failures, may be useful if this caused premature termination. More... | |
| void | cb_set_eval_limit (cb_problemp p, int eval_limit) |
| Sets an upper bound on the number of calls to the oracle (use negative numbers for no limit). More... | |
| void | cb_set_inner_update_limit (cb_problemp p, int update_limit) |
| Set an upper bound on the number of inner updates for the cutting model with primal slacks within one null step (use negative numbers for no limit). More... | |
| void | cb_set_active_bounds_fixing (cb_problemp p, int allow_fixing) |
| If set to true (the default is false), some variables will be fixed automatically to the center value if their bounds are strongly active (i.e., the corresponding multipliers are big). More... | |
| int | cb_get_fixed_active_bounds (cb_problemp p, int *indicator) |
| Returns the indicator vector of variables temporarily fixed to the center value due to significantly positive multipliers for the box constraints, see cb_set_active_bounds_fixing(). More... | |
| void | cb_set_print_level (cb_problemp p, int pril) |
| Specifies the output level (<0 no output at all, =0 errors and warnings, >0 increasingly detailed information) More... | |
Detailed Description
Solve 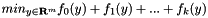 for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here. Internal details are sketched in Internal implementation of the "C" interface.
for convex functions f_i, the y-variables may be bounded or box constrained. The most important steps are explained here. Internal details are sketched in Internal implementation of the "C" interface.
Setting up the Problem, the Functions, and the Main Loop
First open a new problem by calling cb_construct_problem(0) [use cb_construct_prolbem(1) in order to employ a minimal bundle solver with just one aggregate and one new subgradient in each iteration; this is an attractive choice, if fast iterations and/or little memory consumption are of special importance]. The returned pointer of type cb_problemp will be needed for every manipulation of this problem. Once you are done with the problem, however, do not forget to destroy this pointer with cb_destruct_problem().
Next, set the dimension of the design variables/argument as well as possible box constraints on these by the function cb_init_problem().
Now set up your functions f_i as functions of type cb_functionp. Via these functions you will supply, for a given argument, the function value and a subgradient (=the gradient if the function is differentiable) to the solver.
The cb_functionp representations have to be added to the solver using the routine cb_add_function().
Once all functions are added, the optimization process can be started. If you know a good starting point then set it with cb_set_new_center_point() now, otherwise the method will pick the zero vector or, in the case of box constraints, the point closest to zero as starting point.
Finally, set up a loop that calls cb_do_descent_step() until cb_termination_code() is nonzero.
Setting up the Problem, the Functions, and the Main Loop
After the first call to cb_do_descent_step() you can retrieve, at any time, the current objective value by cb_get_objval() and the argument leading to this value by cb_get_center(). For some screen output, use cb_set_print_level().
Lagrangean Relaxation, Primal Approximations, and Cutting Planes
If you are optimizing a Lagrangean relaxation, you might be interested in getting an approximation to your primal optimal solution. This can be done by specifying in each function for each (epsilon) subgradient the corresponding primal vectors that generate it, see cb_functionp and cb_add_function() as a start. Then for each of your functions, you can retrieve the current primal approximation using cb_get_approximate_primal().
If, in addition, you plan to improve your primal relaxation via cutting planes, that are strongly violated by the current primal approximation, you should have a look at cb_append_variables(), cb_subgextp, cb_reinit_function_model(), cb_get_approximate_slacks(), and cb_delete_variables().
Typedef Documentation
◆ cb_functionp
| typedef int(* cb_functionp) ( void *function_key, double *arg, double relprec, int max_subg, double *objective_value, int *n_subgrads, double *subg_values, double *subgradients, double *primal) |
function oracle; describe your function as a function of this type to pass it to the solver
The oracle interface is used to describe a convex function. The dimension of the argument vector of the function must be set in cb_init_problem(), let it be m in the following.
If the sum of several such functions is to be minimized, it is the task of the user to guarantee that all dimensions match.
In many applications, computing the function value is an iterative process that approaches the true function value from below. The code offers a bound for the function value, above which it is certain that the code will reject the current point. If in the iterative process a lower bound on the function value exceeds this bound, then it is sufficient to return, instead of the true function value and a subgradient, the current lower bound and a vector so that together they describe a supporting hyperplane (an epsilon subgradient, lying completely below the function) to the function at this point.
If the function corresponds to Lagrangean relaxation of a primal maximization problem one may want to generate a primal approximate solution. In this case, set in cb_add_function() the desired primal dimension. Then the solver will provide memory in primal for returning in the function the generating primal vectos for each subgradient. If the primal dimension is set to zero, primal will be NULL and no aggregation takes place.
If primal aggregation is used then it is possible to implement a primal cutting plane framework. This requires the introduction of new (dual) variables in the design space of the function. In this case a function of type cb_subgextp (see below) should be provided for filling in the missing coordinates in existing subgradients. This function need not be specified even if constraints are added, but then the cutting model of the objective is lost at each addition of constraints.
- Parameters
-
[in] function_key void pointer supplied by the user on entering the function. May be useful if multiple copies of the same function are used with parameters [in] arg (pointer to double array of length m) argument of the function (e.g. the Lagrange multipliers) [in] relprec relative precision requirement for objective values that may lead to descent steps (this precision is not required if it is already certain that the function value will be too poor) [in] max_subg at most max_subg epsilon-subgradients and subg_values may be returned, but at least one must be returned! [in,out] objective_value (pointer to a double of the caller) - on input: value gives the threshold for a null step; you may stop, if a cutting plane yields at least this;
- on output: return an upper bound on the true function value within relprec *(abs(objval)+1.), if there is no hyperplane cutting above the threshold specified in objective_value on input. Otherwise the return value should be the max of subg_values.
[out] n_subgrads (pointer to an int of the caller) give the number of epsilon-subgradients returned [out] subg_values (pointer to double array of length max_subg, memory already provided by caller) store for each epsilon subgradient the value at the argument [out] subgradients (pointer to double array of length max_subg * m, memory already provided by caller) Format: s1y1,...,s1ym,s2y1,...,s2ym,... (siyj = coefficient of subgradient i at y-coordinate j) [out] primal (pointer to double array, may be NULL or memory of length n*max_subgalready provided by caller) If the function arises from Lagrangean relaxation and a primal approximation is desired then set the primal dimension in cb_add_function() and return the primal solutions corresponding to the eps-subgradients in the array pointed to by primal. Format: p1x1,..,p1xn,p2x1,...,p2xn,...
- Returns
- 0, all correct
- !=0, failure. This does not necessarily terminate the bundle method. Termination is forced only if no new subgradient is returned.
◆ cb_subgextp
| typedef int(* cb_subgextp) ( void *function_key, double *generating_primal, int n_indices, int *variable_indices, double *new_subgradient_values) |
This routine is not needed unless variabls (constraints in Lagrangean relaxation) are added on the fly.
The solver calls this routine whenever new variables have been added on the fly in order to extend old subgradients to the new coordinates. If primal data was supplied for the subgradients then generating_primal holds a pointer to this (possibly aggregated) data, otherwise it is NULL.
In the presence of primal data, the new coordinates correspond to the violation of the new primal constraints. These have to be returned in the array new_subgradient_values; more precisely, for i=0 to n_indices-1 the element new_subgradient_values[i] has to hold the subgradient information of constraint variable_indices[i];
If generating_primal is NULL, then the routine can only successfully extend the subgradients, if the new coordinates have no influence on the function; then the new subgradient coordinates are all zero and the components of new_subgradient_values have to be initialized to zero.
If you do indeed need this, you have to provide one such function with each evaluation function.
- Parameters
-
[in] function_key void pointer supplied by the user on entering the function. May be useful if multiple copies of the same function are used with parameters [in] generating_primal (NULL or pointer to double array of primal length n) if not Null it holds the (possibly aggregated) primal solution that generated the subgradient that needs to be extendend [in] n_indices (int) gives the number of indices for which the subgradient value has to be computed [in] variable_indices (pointer to int array of length n_indices) for the y variables with indices variable_indices[i], i=0,..,@ n_indices-1 the subgradient coefficient has to be computed [out] new_subgradient_values (pointer to double array of length n_indices provided by caller) store the the subgradient coefficient of y variable with index variable_indices[i] at new_subgradient_values[i] for i=0,..,@ n_indices-1
- Returns
- 0 on success,
- 1 if extension is impossible
Function Documentation
◆ cb_add_function()
| int cb_add_function | ( | cb_problemp | p, |
| void * | function_key, | ||
| cb_functionp | f, | ||
| cb_subgextp | se, | ||
| int | primaldim | ||
| ) |
Adds the function, the sum of which should be minimized, to the problem description.
Each function added must be given a unique function_key (this may be the address of the function [if unique], an index, or some parameter information), f supplies the evaluation function and must not be zero, se can be used to specify a routine for extending subgradients, but it may be NULL. primaldim can be used if an approximate primal solution should be aggregated (In this case storage will be supplied in the call to the evaluation function for storing for each subgradient the generating primal vector). It may be zero if this is not needed.
- Parameters
-
[in] p (cb_problemp) pointer to the problem to which the function should be added [in] function_key (void *) The value of the funciton_key must UNIQUELY identify the function, (it may be the address of the funciton [if unique], or give the address of a struct holding additional user parameters) [in] f (cb_functionp) The pointer to the function [in] se (cb_subgextp) This parameter my be NULL, otherwise the respective function will be called in order to compute coefficients for new subgradient coordinates resulting from added variables. [in] primaldim (int) May be zero, otherwise in each call to f enough storage will be provided to store a primal generating vector for each subgradient returned. The primal solutions will be aggregated along with the subgradients. This allows to generate approximate primal optimal solutions, e.g., in Lagrangean relaxation.
- Returns
- 0 on success
- != 0 otherwise
◆ cb_append_variables()
| int cb_append_variables | ( | cb_problemp | p, |
| int | n_append, | ||
| double * | lower_bound, | ||
| double * | upper_bound | ||
| ) |
Append new variables (always in last postions in this order).
If 0 is feasible for the new coordinates then this is selected as starting value for the new coordinates; otherwise, the number closest to zero is used. If all new coordinates can be set to zero then it is assumed that for an existing center point the function values need not be recomputed (this is e.g. the case in Lagrangean relaxation; if this is not correct call cb_reinit_function_model() below). Otherwise the old function values will be marked as outdated and will be recomputed at the next call to e.g. cb_do_descent_step().
- Attention
- Be sure to update your objective functions so that they can handle the new variables before you call this and any further ConicBundle routines that require function evaluations. Also, these operations may lead to inavailability of certain other data such as subgradients and primal approximations.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] n_append (int) number of variables to append (always in last position in the same order) [in] lower_bound (NULL or pointer to double array of size n_append) If NULL, all appended variables are considered unbounded below, otherwise lowerb[i] gives the minimum feasible value for variable y[i], use cb_get_minus_infinity() for unbounded below. [in] upper_bound (NULL or pointer to double array of size n_append) If NULL, all appended variables are considered unbounded above, otherwise lowerb[i] gives the minimum feasible value for variable y[i], use cb_get_plus_infinity() for unbounded below.
- Returns
- 0 on success
- != 0 otherwise
◆ cb_clear()
| void cb_clear | ( | cb_problemp | p | ) |
Clears all data structures and problem information but keeps ouptut settings and algorithmic parameter settings.
- Parameters
-
[in] p (cb_problemp) pointer to the cureent problem
◆ cb_clear_fail_counts()
| void cb_clear_fail_counts | ( | cb_problemp | p | ) |
clears all fail counts on numerical function oder model failures, may be useful if this caused premature termination.
- Parameters
-
[in] p (cb_problemp) pointer to the problem
◆ cb_construct_problem()
| cb_problemp cb_construct_problem | ( | int | no_bundle | ) |
Creates a a new problem object and returns a pointer to it.
- Parameters
-
[in] no_bundle if nonzero, then the minimal bundle consisting of just one new and one aggregate gradient is used so that there is no real bundle available and bundle size options are then meaningless.
- Returns
- ==0, construction of problem object failed
- !=0, pointer to the problem object
◆ cb_delete_variables()
| int cb_delete_variables | ( | cb_problemp | p, |
| int | n_del, | ||
| int * | delete_indices, | ||
| int * | map_to_old | ||
| ) |
Deletes variables corresponding to the specified indices.
The indices of the remaining variables are reassigned so that they are consecutive again, the routine returns in map_to_old a vector giving for each new index of these remaining variables the old coordinate. The memory for map_to_old has to be provided by the caller, who has also to guarantee that it is long enough!
If all of the deleted variables are zero, function values are assumed to remain correct (if this is not so, call cb_reinit_function_model() below) Otherwise the old function values will be marked as outdated and will be recomputed at the next call to e.g. cb_do_descent_step().
- Attention
- Be sure to update your objective functions so that they can handle the new variables before you call any further ConicBundle routines that require function evaluations. Also, these operations may lead to inavailability of certain other data such as subgradients and primal approximations.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] n_del (int) number of variables to be deleted [in] delete_indices (pointer to int array of length n_del) the entries delete_indices[i] with i=0,...,n_del-1 specify the indices of the variables to be deleted [out] map_to_old (pointer to int array of length cb_get_dim()-n_del provided by the caller) after the call element map_to_old[i] gives the old index (before the call) of the variable that now has index position i.
- Returns
- 0 on success
- != 0 otherwise
◆ cb_destruct_problem()
| int cb_destruct_problem | ( | cb_problemp * | p | ) |
Destructs and frees the problem object.
- Parameters
-
[in,out] p (cb_problemp*) address of the main pointer to the problem that should be destructed. the problem pointer will be set to zero upon successful destruction
- Returns
- 0, all correct
- >0, failure
◆ cb_get_approximate_primal()
| int cb_get_approximate_primal | ( | cb_problemp | p, |
| void * | function_key, | ||
| double * | primal | ||
| ) |
Returns the current approximate primal solution for the function having this function_key.
The function_key must match the one specified in cb_add_function(). Likewise, the routine is meaningful only if primaldim was set in cb_add_function() and primal vectors were returned along with the subgradients in all calls to cb_functionp with this function_key. In this case it returns the current approximate primal solution aggregated alongside with the aggregate subgradient. A primal solution may not be available after addition of constraints, if extension of the aggregate subgradient to the new coordinates failed.
If no primal dimension was set for this function, the routine does nothing.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function() [out] primal (pointer to double array of length @ primaldim provided by caller) primal[i] will be filled with the coordinate value i
- Returns
- 0 on success
- != 0 otherwise
◆ cb_get_approximate_slacks()
| int cb_get_approximate_slacks | ( | cb_problemp | p, |
| double * | slacks | ||
| ) |
Returns the multipliers for the bound constraints on the design variables; in Lagrangean relaxation they may be interpreted as primal slacks for inequality constraints.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [out] slacks (pointer to double array of length cb_get_dim() provided by caller) slacks[i] will be filled with the coordinate value i
- Returns
- 0 on success
- != 0 otherwise
◆ cb_get_bundle_parameters()
| int cb_get_bundle_parameters | ( | cb_problemp | p, |
| void * | function_key, | ||
| int * | max_modelsize, | ||
| int * | max_bundelsize | ||
| ) |
Retrieves the two bundle parameters specified in the routines cb_set_max_modelsize() and cb_set_max_bundlesize(). for the function having this function_key.
The function_key must match the one specified in cb_add_function().
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function() [out] max_modelsize (pointer to int) returns the maximum number of subgradients to be used in forming the cutting model [out] max_bundelsize (pointer to int) returns maximum number of subgradients stored for use in formint the cutting model
- Returns
- 0 on success
- != 0 otherwise
◆ cb_get_candidate()
| int cb_get_candidate | ( | cb_problemp | p, |
| double * | candidate | ||
| ) |
Returns the last point, the "candidate", at which the function was evaluated in cb_do_descent_step().
If this evaluation lead to a descent step, it is the same point as in cb_get_center().
- Parameters
-
[in] p (cb_problemp) pointer to the problem [out] candidate (pointer to double array of length cb_get_dim() provided by caller) center[i] will be the value of design variable y_i of the point
- Returns
- 0 on success
- != 0 otherwise
◆ cb_get_candidate_primal()
| int cb_get_candidate_primal | ( | cb_problemp | p, |
| void * | function_key, | ||
| double * | primal | ||
| ) |
Returns the best primal solution returned by the last evaluation of the function having this function_key in the point cb_get_candidate().
The function_key must match the one specified in cb_add_function(). Likewise, the routine is meaningful only if primaldim was set in cb_add_function() and primal vectors were returned along with the subgradients in calls to cb_functionp with this function_key. If no primal dimension was set for this function, the routine does nothing.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function() [out] primal (pointer to double array of length @ primaldim provided by caller) primal[i] will be filled with the coordinate value i
- Returns
- 0 on success
- != 0 otherwise
◆ cb_get_candidate_value()
| double cb_get_candidate_value | ( | cb_problemp | p | ) |
Returns the objective value computed in the last step of do_descent_step(), independent of whether this was a descent step or a null step (initially undefined).
If no problem modification routines were called since then, it is the objective value at the point returned by cb_get_candidate(). If this last evaluation led to a descent step, then it is the same value as in get_objval().
◆ cb_get_center()
| int cb_get_center | ( | cb_problemp | p, |
| double * | center | ||
| ) |
Returns the next center point that was produced by the last call to cb_do_descent_step (in some problem modification routines the center point may be updated immediately, in others the center point will be corrected automatically directly before starting the next descent step and its values may be infeasible till then).
- Parameters
-
[in] p (cb_problemp) pointer to the problem [out] center (pointer to double array of length cb_get_dim() provided by caller) center[i] will be the value of design variable y_i in the next center point (mostly the result of the latest descent step)
- Returns
- 0 on success
- != 0 otherwise
◆ cb_get_center_primal()
| int cb_get_center_primal | ( | cb_problemp | p, |
| void * | function_key, | ||
| double * | primal | ||
| ) |
Returns the best primal solution obtained in the current center point in evaluating the function having this function_key.
The function_key must match the one specified in cb_add_function(). Likewise, the routine is meaningful only if primaldim was set in cb_add_function() and primal vectors were returned along with the subgradients in calls to cb_functionp with this function_key. If no primal dimension was set for this function, the routine does nothing.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function() [out] primal (pointer to double array of length @ primaldim provided by caller) primal[i] will be filled with the coordinate value i
- Returns
- 0 on success
- != 0 otherwise
◆ cb_get_fixed_active_bounds()
| int cb_get_fixed_active_bounds | ( | cb_problemp | p, |
| int * | indicator | ||
| ) |
Returns the indicator vector of variables temporarily fixed to the center value due to significantly positive multipliers for the box constraints, see cb_set_active_bounds_fixing().
Such a fixing indicates that the corresponding variables would like to stay at their bounds. If no variables were fixed, the dimension of the vector is zero.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [out] indicator (pointer to int array of length cb_get_dim() @ provided by caller) indicator[i] will be 1 if the variable i was fixed to the bound and 0 otherwise
- Returns
- 0 on success
- != 0 otherwise
◆ cb_get_function_status()
| int cb_get_function_status | ( | cb_problemp | p, |
| void * | function_key | ||
| ) |
Returns the return value of the latest evaluation call to the function with this function_key.
Remember, a unique function_key must be specified in cb_add_function().
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function()
- Returns
- return value of latest call to the function having this function_key
◆ cb_get_last_weight()
| double cb_get_last_weight | ( | cb_problemp | p | ) |
Returns the current weight for the quadratic term in the augmented subproblem (may be interpreted as 1./step_size or 1./trustregion-radius).
- Parameters
-
[in] p (cb_problemp) pointer to the problem
- Returns
- double weight value
◆ cb_get_objval()
| double cb_get_objval | ( | cb_problemp | p | ) |
Returns the objective value resulting from last descent step (initially undefined).
If no problem modification routines were called since then, it is the objective value at the point returned by cb_get_center().
- Parameters
-
[in] p (cb_problemp) pointer to the problem
- Returns
- double objective value
◆ cb_get_sgnorm()
| double cb_get_sgnorm | ( | cb_problemp | p | ) |
Returns Euclidean norm of the latest aggregate subgradient.
- Parameters
-
[in] p (cb_problemp) pointer to the problem
- Returns
- norm of the latest aggregate subgradient
◆ cb_get_subgradient()
| int cb_get_subgradient | ( | cb_problemp | p, |
| double * | subgradient | ||
| ) |
Returns the latest aggregate subgradient.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [out] subgradient (pointer to double array of length cb_get_dim() provided by caller) subgradient[i] will be filled with the coordinate value i
- Returns
- 0 on success
- != 0 otherwise
◆ cb_init_problem()
| int cb_init_problem | ( | cb_problemp | p, |
| int | m, | ||
| double * | lowerb, | ||
| double * | upperb | ||
| ) |
Initializes the problem by setting the design space (the dimension and possible box constraints of the variables)
Clears all data structures and sets the dimension @ m for a new problem. for solving min_{y in R^m} f_0(y) + f_1(y) + ... Box constraints may be specified for y, the functions f_i must be added by cb_add_function().
Lower and/or upper bounds must be speicified for all variables or for none of them. To specify no bounds at all, give Null pointers. Otherwise use cb_get_minus_infinity() for unbounded below and cb_get_plus_infinity() for unbounded above. For NULL pointers, unbounded will be used as default for all variables. Specifying bounds selectively is also possible by cb_set_lower_bound() or cb_set_upper_bound().
- Parameters
-
[in] p (cb_problemp) pointer to the current problem [in] m (int) the dimension of the argument/design space/the number of Lagrange multipliers [in] lowerb (either pointer to double array of length m or NULL) If NULL, all variables are considered unbounded below, otherwise lowerb[i] gives the minimum feasible value for variable y[i], use cb_get_minus_infinity() for unbounded below. [in] upperb (either pointer to double array of length m or NULL) If NULL, all variables are considered unbounded above, otherwise upperb[i] gives the maximum feasible value for variable y[i], use cb_get_plus_infinity() for unbounded above.
- Returns
- 0 on success
- != 0 otherwise
◆ cb_print_termination_code()
| int cb_print_termination_code | ( | cb_problemp | p | ) |
Outputs a text version of termination code, see cb_termination_code().
- Parameters
-
[in] p (cb_problemp) pointer to the problem
- Returns
- 0 on success
- != 0 otherwise
◆ cb_reassign_variables()
| int cb_reassign_variables | ( | cb_problemp | p, |
| int | n_assign, | ||
| int * | assign_new_from_old | ||
| ) |
Reassigns variables to new index positions by mapping to position i the variable that previously had index assign_new_from_old[i].
Old variables, that are not mapped to any position will be deleted. It is allowed to generate several copies of old variables.
If all of the deleted variables as well as new multiple copies are zero, function values are assumed to remain correct (if this is not so, call cb_reinit_function_model() below). Otherwise the old function values will be marked as outdated and will be recomputed at the next call to e.g. cb_do_descent_step().
- Attention
- Be sure to update your objective functions so that they can handle the new variables before you call any further ConicBundle routines that require function evaluations. Also, these operations may lead to inavailability of certain other data such as subgradients and primal approximations.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] n_assign (int) number of variables after reassignment [in] assign_new_from_old (pointer to int array of length n_assign) entry assign_new_from_old[i] with i=0,...,n_assign-1 specifies the old index of the variable, that has to be copied to index position i.
- Returns
- 0 on success
- != 0 otherwise
◆ cb_reinit_function_model()
| int cb_reinit_function_model | ( | cb_problemp | p, |
| void * | function_key | ||
| ) |
Clears cutting model, subgradients and stored function values for the function with this function_key.
This has to be called whenever the specified function was modified so that the old subgradients and/or primal generators are no longer valid.
The function_key must match the one specified in cb_add_function().
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function()
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_active_bounds_fixing()
| void cb_set_active_bounds_fixing | ( | cb_problemp | p, |
| int | allow_fixing | ||
| ) |
If set to true (the default is false), some variables will be fixed automatically to the center value if their bounds are strongly active (i.e., the corresponding multipliers are big).
The coordinates to be fixed are redetermined in each call following a descent step or a change of the function. An indicator vector of the variables fixed in the last call can be obtained via the routine cb_get_fixed_active_bounds().
Setting this value to true might improve the performance of the algorithm in some instances but there is no convergence theory. It might be particularly helpful within Lagrangian relaxation if a primal cutting plane approach is used and non-tight inequalities should be eliminated quickly (fixing then indicates large primal slack values).
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] allow_fixing (0 or 1)
◆ cb_set_defaults()
| void cb_set_defaults | ( | cb_problemp | p | ) |
Sets default values for algorithmic parameters that are not function specific (e.g., relative precision, weight and weight bounds for the augmentedproblem, etc.)
- Parameters
-
[in] p (cb_problemp) pointer to the cureent problem
◆ cb_set_eval_limit()
| void cb_set_eval_limit | ( | cb_problemp | p, |
| int | eval_limit | ||
| ) |
Sets an upper bound on the number of calls to the oracle (use negative numbers for no limit).
If this number is reached, the algorithm will terminate independently of whether the last step was a descent or a null step. A negative number will be interepreted as no limit.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] eval_limit (int)
◆ cb_set_inner_update_limit()
| void cb_set_inner_update_limit | ( | cb_problemp | p, |
| int | update_limit | ||
| ) |
Set an upper bound on the number of inner updates for the cutting model with primal slacks within one null step (use negative numbers for no limit).
A negative number will be interepreted as no limit, i.e., the updates will be done till a certain precision of the cutting model is achieved.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] update_limit (int)
◆ cb_set_lower_bound()
| int cb_set_lower_bound | ( | cb_problemp | p, |
| int | i, | ||
| double | lower_bound | ||
| ) |
set lower bound for variable i, use cb_get_minus_infinity() for unbounded from below.
The algorithm may have to adapt the center point aftwards. In this case the old function values will be marked as outdated and will be recomputed at the next call to e.g. cb_do_descent_step().
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] i (int) index of the variable [in] lower_bound (double) value of the lower bound on variable i
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_max_bundlesize()
| int cb_set_max_bundlesize | ( | cb_problemp | p, |
| void * | function_key, | ||
| int | bundlesize | ||
| ) |
Sets the maximum number of subgradients stored for use in forming the model or determining metric information of the function having this function_key. it must be as least as large as max_modelsize (and is increased to this if not)
The function_key must match the one specified in cb_add_function().
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function() [in] bundlesize (int) maximum number of subgradients to be used in forming the cutting model
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_max_modelsize()
| int cb_set_max_modelsize | ( | cb_problemp | p, |
| void * | function_key, | ||
| int | modelsize | ||
| ) |
Sets the maximum number of subgradients used in forming the cutting model of the function having this function_key.
The function_key must match the one specified in cb_add_function().
Quite often a very small model, e.g., 2, yields very fast iterations and good progress in time (sometimes at the cost of more evaluations). By limited numerical experience, a significant reduction in the number of evaluations can only be expected if the bundle is large enough to wrap the function rather tightly. Quite frequently, unfortunately, this entails that solving the quadratic subproblems is more expensive than function evaluation.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function() [in] modelsize (int) maximum number of subgradients to be used in forming the cutting model
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_max_new_subgradients()
| int cb_set_max_new_subgradients | ( | cb_problemp | p, |
| void * | function_key, | ||
| int | max_new_subg | ||
| ) |
Sets the maximum number of epsilon subgradients that can be returned in one call to the function having this function_key.
The function_key must match the one specified in cb_add_function().
The parameter max_new_subg corresponds directly to the parameter max_subg in cb_functionp.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] function_key (void *) unique identifier as set in cb_add_function() [in] max_new_subg (int) maximum number of new epsilon subgradients to be returned in an evaluation call to the function
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_max_weight()
| int cb_set_max_weight | ( | cb_problemp | p, |
| double | max_weight | ||
| ) |
Sets an upper bound on the weight for the quadratic term of the augmented subproblem.
Nonpositive values indicate no bound. The new value shows its effect only at first dynamic change of the weight.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] max_weight (double)
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_min_weight()
| int cb_set_min_weight | ( | cb_problemp | p, |
| double | min_weight | ||
| ) |
Sets a lower bound on the weight for the quadratic term of the augmented subproblem.
Nonpositive values indicate no bound. The new value shows its effect only at first dynamic change of the weight.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] min_weight (double)
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_new_center_point()
| int cb_set_new_center_point | ( | cb_problemp | p, |
| double * | center | ||
| ) |
Set the starting point/center that will be used in the next call to cb_do_descent_step(). Each call to this routine causes an immediate evaluation of all oracles.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] center (pointer to double array of length cb_get_dim()) center[i] holds the value of design variable y_i
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_next_weight()
| int cb_set_next_weight | ( | cb_problemp | p, |
| double | weight | ||
| ) |
Sets the weight (>0) to be used in the quadratic term of the next augmented subproblem (may be interpreted as 1./step_size or 1./trustregion-radius).
Independent of whether the weight violates current min- and max-bounds set in cb_set_min_weight() and cb_set_max_weight(), the next model will be computed for this value. Thereafter, however, it will be updated as usual; in particular, it may be truncated by min and max bounds immediately after the first subproblem.
In order to guarantee a constant weight (e.g. 1 is frequently a reasonable choice if the automatic default heuristic performs poorly), set the min and max bounds to the same value, too.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] weight (double)
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_print_level()
| void cb_set_print_level | ( | cb_problemp | p, |
| int | pril | ||
| ) |
Specifies the output level (<0 no output at all, =0 errors and warnings, >0 increasingly detailed information)
Output levels:
- <0 ... no output, not even errors or warnings
- 0 ... no output except for errors and warnings
- 1 ... line summary after each descent step
- >1 ... undocumented and increasingly detailed log information. These higher levels should only be used if requested for debugging purposes.
Example for level 1:
00:00:00.00 endit 1 1 1 563. 563. 39041.188 39043.162 00:00:00.00 endit 2 2 2 563. 559. 38488.165 38490.200 00:00:00.00 endit 3 3 3 56.3 555. 33014.533 33211.856 00:00:00.00 endit 4 4 4 5.63 517. -14306.459 2738.0343 00:00:00.00 endit 5 5 5 4.04 148. -2692.1131 2.2150883 00:00:00.00 endit 6 6 6 4.01 1.29 1.7908952 2.0000581 00:00:00.00 endit 7 7 7 3.95 0.0213 1.9999387 2.0000000 00:00:00.00 _endit 8 8 8 3.95 2.94e-05 2.0000000 2.0000000 Column 1 2 3 4 5 6 7 8 9
- Column 1: computation time in hh:mm:ss.dd,
- Column 2: "endit" is convenient for grep and stands for "end of iteration". Iterations with cb_termination_code()!=0 are marked with "_endit".
- Column 3: number of descent steps (= calls to cb_do_descent_step())
- Column 4: number of descent and null steps. Up to initialization calls and reevaluations, this is the number of evaluation calls to the function oracles from within the bundle method. In the example all calls led to descent steps.
- Column 5: number of innermost iterations. It differs from column 5 only in the case of variables with bounds in which case it gives the number of updates of the multipliers for the bounds (or primal slacks in Lagrangean relaxation). Exceedingly high numbers in this column indicate that some variables are constantly at their bounds and it might be possible to improve convergence by deleting them (i.e. set them as constants to this bound and remove the variable).
- Column 6: the weight of the quadratic term in the augmented problem.
- Column 7: the norm of the aggregate subgradient. If it is small, say below 0.1, then mostly this is good indication that the objective value is close to optimal.
- Column 8: the value of the cutting model in the last candidate point. It is always a lower bound on the true function value in this point
- Column 9: the objective value in the latest point that led to a descent step, i.e., the point returend by cb_get_center(). Whenever cb_termination_code() returns 0 this is also the objective value of the latest evaluation call to the function oracles and the value in the center point of the next iteration.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] pril (int) print level
◆ cb_set_term_relprec()
| int cb_set_term_relprec | ( | cb_problemp | p, |
| double | term_relprec | ||
| ) |
Sets the relative precision requirements for successful termination (default 1e-5).
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] term_relprec (double) The algorithm stops with termination code 1, if predicted progress for the next step is less than term_relprec times absolute function value plus one.
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_upper_bound()
| int cb_set_upper_bound | ( | cb_problemp | p, |
| int | i, | ||
| double | upper_bound | ||
| ) |
set upper bound for variable i, use cb_get_plus_infinity() for unbounded above.
The algorithm may have to adapt the center point aftwards. In this case the old function values will be marked as outdated and will be recomputed at the next call to e.g. cb_do_descent_step().
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] i (int) index of the variable [in] upper_bound (double) value of the upper bound on variable i
- Returns
- 0 on success
- != 0 otherwise
◆ cb_set_variable_metric()
| int cb_set_variable_metric | ( | cb_problemp | p, |
| int | do_variable_metric | ||
| ) |
Use a variable metric heuristic or switch it off alltogether. (the variable metric heuristic resets the quadratic term to some diagonal or low rank matrix, switching it off resets the proximal term to the identity)
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] do_variable_metric (int) - 0 switch off the scaling heuristic
- 1 use a diagonal scaling heuristic
- 2 use a diagonal scaling heuristic combined with one for the bounds
- Returns
- 0 on success
- != 0 otherwise
◆ cb_solve()
| int cb_solve | ( | cb_problemp | p, |
| int | maxsteps, | ||
| int | stop_at_descent_steps | ||
| ) |
solves or does a prescribed number of
Bundle methods solve a problem by a sequence of so called descent steps that actually bring progress by moving from the current "center point" to a new center with better objective. A descent step may consist of several function evaluations (null steps), that lead to no immediate progress but mainly improve a cutting model of the objective function close to the current center point. A minimizer to the model is accepted as descent step if the function value at this point satisfies a sufficient decrease criterion in comparison to the decrease predicted by the model. Having found a descent step, the next center is automatically shifted to this successful candidate. Termination criteria may stop the process of seeking for a descent step, in which case the current center is kept and the routine termination_code() returns the termination code.
Restarting, after each descent step, the bundle method from scratch with the new center as starting point does not endanger convergence. Therefore, a descent step is the smallest unit, after which user interaction can take place safely. To allow this there is a flag stop_at_descent_steps that will cause the code to return after the next descent step.
If you know what your are doing, you may also use the input parameter maxsteps to force the algorithm to return after at most maxsteps null steps. Calling solve again without any intermediate problem configurations will then simply continue the process where it stopped and convergence is save. During null steps one may not decrease the weight or delete nonzero variables of the center or the current candidate!
In a Lagrangean relaxation cutting plane approach one may want to separate and enlarge the dimension after a certain number of null steps. In this case the code will try to preserve the model, given appropriate subgradient extension routines have been provided. If the model cannot be extended, it has to be discarded (if subgradient extension is not successful this is done automatically), and the algorithm will be restarted from the current center point.
- Parameters
-
[in] p (cb_problemp) pointer to the problem [in] maxsteps (int) use value =0 as default (anything <= serves as infinite upper bound), if maxsteps>0 the code returns after at most so many null steps [in] stop_at_descent_steps (int) if true(!=0) the code also returns whenever a descent step occured, if false(==0) it only stops after maxsteps or when a termination criterion is met
- Returns
- 0 on success
- != 0 otherwise
◆ cb_termination_code()
| int cb_termination_code | ( | cb_problemp | p | ) |
Returns the termination code of the bundle algorithm for the latest descent step.
For resetting all counters relevant for termination see cb_clear_fail_counts() .
- Returns
- 0 : Not terminated. (Continue with the next cb_do_descent_step())
- 1 : Relative precision criterion satisfied. (See cb_set_term_relprec())
- 2 : Timelimit exceeded. (Currently the C interface does not offer a timelimit.)
- 4 : Maximum number of function reevaluations exceeded. (Indicates that there is a problem with one of the function oracles that seems to deliver no valid upper bounds on the true function value for descent steps)
- 8 : Maximum number of quadratic subproblem failures exceeded. (Indicates that the numerical limits of the inner quadratic programming solver are reached, no further progress expected)
- 16 : maximum number of model evaluation failures exceeded (Indicates that the numerical limits of the setup of the subproblem are reached, no further progress expected)
- 32 : maximum number of failures to increase the augmented model value exceeded (Indicates that the numerical limits of the interplay between subproblem and quadratic programming solver are reached, no further progress expected)
- 64 : maximum number of oracle calls (function evaluations) exceeded, see cb_set_eval_limit()
- 128 : maximum number of oracle failures exceeded. This refers to function evaluations that terminate with insufficient precision but still provide a new approximate subgradient. A failure typically indicates numerical difficulties with the precision requirements. (Currently the interface does not allow to manipulate the limit, it is set to 10)
 1.8.13
1.8.13