defines the abstract interface for QPSolverBasicStructures that the basic routines there need to access the cost and constraint data; it also defines the interface to QPSolverBasicStructures, how to call those routines and how to retrieve the results. More...
#include <QPSolverBasicStructures.hxx>
Public Member Functions | |
| virtual | ~QPSolverBasicInterface () |
| virtual destructor | |
interface for QPSolverBasicStructures for getting the data | |
| virtual CH_Matrix_Classes::Integer | QPget_xdim () const =0 |
| dimension of the quadratic variable x | |
| virtual CH_Matrix_Classes::Integer | QPget_ydim () const =0 |
| dimension of the dual variables to the linear constraints (number of rows of A) | |
| virtual CH_Matrix_Classes::Matrix & | QPadd_Qx (const CH_Matrix_Classes::Matrix &vecin, CH_Matrix_Classes::Matrix &vecout) const =0 |
| vecout += quadratic term * vecin | |
| virtual CH_Matrix_Classes::Matrix & | QPadd_Ax (const CH_Matrix_Classes::Matrix &xin, CH_Matrix_Classes::Matrix &outplusAx) const =0 |
| outplusAx += A * xin | |
| virtual CH_Matrix_Classes::Matrix & | QPadd_Aty (const CH_Matrix_Classes::Matrix &yin, CH_Matrix_Classes::Matrix &outplusAty) const =0 |
| outplusAty += transpose(A) * yin | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_c () const =0 |
| returns the linear cost vector for the quadratic variable x | |
| virtual CH_Matrix_Classes::Real | QPget_gamma () const =0 |
| returns a potential constant offset of the cost function | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_rhslb () const =0 |
| returns rhslb of rhslb <= Ax | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_rhsub () const =0 |
| returns rhsub of Ax <= rhsub | |
| virtual const CH_Matrix_Classes::Indexmatrix & | QPget_rhslbind () const =0 |
| returns the indices where rhslb is not minus infinity (sorted increasingly) | |
| virtual const CH_Matrix_Classes::Indexmatrix & | QPget_rhsubind () const =0 |
| returns the indices where rhsub is not plus infinity (sorted increasingly) | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_lb () const =0 |
| returns lb of lb <= x | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_ub () const =0 |
| returns ub of x <= ub | |
| virtual const CH_Matrix_Classes::Indexmatrix & | QPget_lbind () const =0 |
| returns the indices where lb is not minus infinity (sorted increasingly) | |
| virtual const CH_Matrix_Classes::Indexmatrix & | QPget_ubind () const =0 |
| returns the indices where ub is not plus infinity (sorted increasingly) | |
interface for calling the routines and querying the result of QPSolverBasicStructures | |
| virtual void | QPIclear ()=0 |
| reset all values of the internal basic structures and variables | |
| virtual int | QPset_solver_parameters (QPSolverParameters *params)=0 |
| pass on new parameters, ownership is tranferred to this, will be deleted here | |
| virtual int | QPset_startx (const CH_Matrix_Classes::Matrix &startx)=0 |
| set a starting value for the quadratic variables | |
| virtual int | QPset_starts (const CH_Matrix_Classes::Matrix &starts)=0 |
| set a starting value for the slack variables of the constraints | |
| virtual int | QPset_starty (const CH_Matrix_Classes::Matrix &starty)=0 |
| set a starting value for the dual variables of the constraints | |
| virtual int | QPset_startzlb (const CH_Matrix_Classes::Matrix &startlb)=0 |
| set a starting value for the dual variables of the lower bounds on the quadratic variables | |
| virtual int | QPset_startzub (const CH_Matrix_Classes::Matrix &startub)=0 |
| set a starting value for the dual variables of the upper bounds on the quadratic variables | |
| virtual int | QPset_startmu (CH_Matrix_Classes::Real startmu)=0 |
| set a starting value for the barrier parameter mu | |
| virtual int | QPIsolve (bool reinitialize=true, CH_Matrix_Classes::Real skip_factor=-1.)=0 |
| solve the problem to the precision specified by the parameters; if the problem is resolved for slightly modified cost data (the feasible set should not change), setting reinitialize=false and a skip_factor for previous "central path" solutions might help to speed up the resolve | |
| virtual CH_Matrix_Classes::Real | QPget_primalval () const =0 |
| after QPIsolve, retrieve the primal objective value (of the quadratic variables) | |
| virtual CH_Matrix_Classes::Real | QPget_dualval () const =0 |
| after QPIsolve, retrieve the dual objective value (quadratic and dual variables) | |
| virtual QPSolverParameters * | QPget_parameters () const =0 |
| return the current parameters for potential modification (do not delete!) | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_x () const =0 |
| return the current value of the quadratic variables (after a successful QPIsolve the optimal solution) | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_y () const =0 |
| return the current value of the dual variables to the constraints (after a successful QPIsolve the optimal solution) | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_zlb () const =0 |
| return the current value of the dual variables to the lower bounds of the quadratic variables (after a successful QPIsolve the optimal solution) | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_zub () const =0 |
| return the current value of the dual variables to the upper bounds of the quadratic variables (after a successful QPIsolve the optimal solution) | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_s () const =0 |
| return the current value of the slack variables of the constraints (after a successful QPIsolve the optimal solution) | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_rhszlb () const =0 |
| return the current value of the dual variables to the lower bounds of the constraints (after a successful QPIsolve the optimal solution) | |
| virtual const CH_Matrix_Classes::Matrix & | QPget_rhszub () const =0 |
| return the current value of the dual variables to the upper bounds of the constraints (after a successful QPIsolve the optimal solution) | |
| virtual CH_Matrix_Classes::Real | QPget_mu () const =0 |
| return the current value of the barrier parameter mu | |
 Public Member Functions inherited from ConicBundle::CBout Public Member Functions inherited from ConicBundle::CBout | |
| virtual void | set_out (std::ostream *out=0, int print_level=1) |
| Specifies the output level (out==NULL: no output at all, out!=NULL and level=0: errors and warnings, level>0 increasingly detailed information) More... | |
| virtual void | set_cbout (const CBout *cb, int incr=-1) |
| Specifies the output level relative to the given CBout class. More... | |
| void | clear_cbout () |
| reset to default settings (out=0,print_level=1) | |
| CBout (const CBout *cb=0, int incr=-1) | |
| calls set_cbout | |
| CBout (std::ostream *outp, int pl=1) | |
| initialize correspondingly | |
| CBout (const CBout &cb, int incr=0) | |
| copy constructor | |
| virtual bool | cb_out (int pl=-1) const |
| Returns true if out!=0 and (pl<print_level), pl<0 should be used for WARNINGS and ERRORS only, pl==0 for usual output. | |
| std::ostream & | get_out () const |
| If cb_out() returned true, this returns the output stream, but it will abort if called with out==0. | |
| std::ostream * | get_out_ptr () const |
| returns the pointer to the output stream | |
| int | get_print_level () const |
| returns the print_level | |
| virtual int | mfile_data (std::ostream &out) const |
| writes problem data to the given outstream | |
Detailed Description
defines the abstract interface for QPSolverBasicStructures that the basic routines there need to access the cost and constraint data; it also defines the interface to QPSolverBasicStructures, how to call those routines and how to retrieve the results.
Ignoring the model part, the routines solve 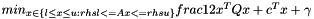
NOTE: as this is taken in part from an independent code, the roles of y and x switch here in comparison to their standard use in ConicBundle.
Q needs to be positive definite. Q and A are supposed to be available by matrix-vector multiplication and the diagonal of Q must be extractable for use in a preconditioner. If the bound constraints are few, they still must be provided in full length, but they may be acessed by indexvectors.
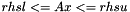 is implemented by introducing an additional variable
is implemented by introducing an additional variable 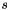 with
with 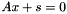 and
and 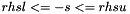 . If in certain componnets the lower and upper bounds are identical,
. If in certain componnets the lower and upper bounds are identical, 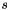 is fixed to this value.
is fixed to this value.
The interpretation of the dual variables may be read of from the Lagrangian 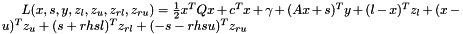
The main entry point is QPIsolve() where I is short for internal; see the general explanations in QPSolverBasicStructures for an outline of the inner workings thereof.
The documentation for this class was generated from the following file:
 1.8.13
1.8.13