abstract class for setting up and solving the primal dual KKT System within QPSolverBasicStructures More...
#include <QPKKTSolverObject.hxx>
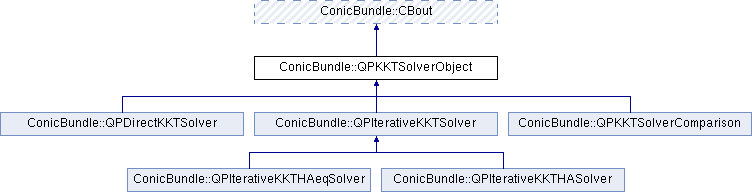
Public Member Functions | |
| virtual void | clear () |
| reset data to empty | |
| QPKKTSolverObject (CBout *cb=0, int cbinc=-1) | |
| default constructor | |
| virtual | ~QPKKTSolverObject () |
| virtual destructor | |
| virtual int | QPinit_KKTdata (QPSolverProxObject *Hp, QPModelBlockObject *model, const CH_Matrix_Classes::Sparsemat *A, const CH_Matrix_Classes::Indexmatrix *eq_indices)=0 |
| returns 1 if this class is not applicable in the current data situation, otherwise it stores the data pointers and these need to stay valid throught the use of the other routines but are not deleted here More... | |
| virtual int | QPinit_KKTsystem (const CH_Matrix_Classes::Matrix &KKTdiagx, const CH_Matrix_Classes::Matrix &KKTdiagy, CH_Matrix_Classes::Real Hfactor, CH_Matrix_Classes::Real prec, QPSolverParameters *params)=0 |
| set up the primal dual KKT system for being solved for predictor and corrector rhs in QPsolve_KKTsystem | |
| virtual int | QPsolve_KKTsystem (CH_Matrix_Classes::Matrix &solx, CH_Matrix_Classes::Matrix &soly, const CH_Matrix_Classes::Matrix &primalrhs, const CH_Matrix_Classes::Matrix &dualrhs, CH_Matrix_Classes::Real rhsmu, CH_Matrix_Classes::Real rhscorr, CH_Matrix_Classes::Real prec, QPSolverParameters *params)=0 |
| solve the KKTsystem to precision prec for the given right hand sides that have been computed for the value rhsmu of the barrier parameter and in which a rhscorr fraction (out of [0,1] of the corrector term have been included; in iterative solvers solx and soly may be used as starting points | |
| virtual CH_Matrix_Classes::Real | QPget_blockH_norm () |
| for judging violation this returns (an estimate of) the norm of the H-row in the latest system | |
| virtual CH_Matrix_Classes::Real | QPget_blockA_norm () |
| for judging violation this returns (an estimate of) the norm of the A-row in the latest system | |
| virtual CH_Matrix_Classes::Integer | QPget_nmult () const |
| for evaluation purposes with iterative solvers, return the number of matrix vector multiplications since the latest call to QPinit_KKTsystem (returns 0 for direct solvers) | |
| virtual CH_Matrix_Classes::Real | QPget_condition_number () |
| for evaluation purposes with iterative solvers, return an estimate of the condition number (returns -1. for direct solvers or if not supplied) | |
| virtual CH_Matrix_Classes::Integer | QPget_precond_rank () |
| for evaluation purposes with iterative solvers, return the rank of the precondiontioner used (or the number of n-vector multiplications per call) | |
| virtual CH_Matrix_Classes::Integer | QPget_system_size () |
| for evaluation purposes with iterative solvers, return the size of the system matrix | |
 Public Member Functions inherited from ConicBundle::CBout | |
| virtual void | set_out (std::ostream *out=0, int print_level=1) |
| Specifies the output level (out==NULL: no output at all, out!=NULL and level=0: errors and warnings, level>0 increasingly detailed information) More... | |
| virtual void | set_cbout (const CBout *cb, int incr=-1) |
| Specifies the output level relative to the given CBout class. More... | |
| void | clear_cbout () |
| reset to default settings (out=0,print_level=1) | |
| CBout (const CBout *cb=0, int incr=-1) | |
| calls set_cbout | |
| CBout (std::ostream *outp, int pl=1) | |
| initialize correspondingly | |
| CBout (const CBout &cb, int incr=0) | |
| copy constructor | |
| virtual bool | cb_out (int pl=-1) const |
| Returns true if out!=0 and (pl<print_level), pl<0 should be used for WARNINGS and ERRORS only, pl==0 for usual output. | |
| std::ostream & | get_out () const |
| If cb_out() returned true, this returns the output stream, but it will abort if called with out==0. | |
| std::ostream * | get_out_ptr () const |
| returns the pointer to the output stream | |
| int | get_print_level () const |
| returns the print_level | |
| virtual int | mfile_data (std::ostream &out) const |
| writes problem data to the given outstream | |
Protected Attributes | |
| QPSolverProxObject * | Hp |
| points to the quadratic cost representation, may NOT be NULL afer init | |
| QPModelBlockObject * | model |
| points to the cutting model information, may be NULL | |
| const CH_Matrix_Classes::Sparsemat * | A |
| points to a possibly present constraint matrix, may be NULL | |
| const CH_Matrix_Classes::Indexmatrix * | eq_indices |
| if not NULL, these rows of A correspond to equations; needed for checking applicability of this Object | |
| CH_Matrix_Classes::Real | blockH_norm |
| for judging violation: (an estimate of) the norm of the H-row in the system | |
| CH_Matrix_Classes::Real | blockA_norm |
| for judging violation: (an estimate of) the norm of the A-row in the system | |
Detailed Description
abstract class for setting up and solving the primal dual KKT System within QPSolverBasicStructures
For initializing such a solver, first call QPinit_KKTdata(), whose arguments must give access to the data objects describing the basic problem data of all KKT Systems in this call to the QP solver. QPinit_KKTdata() is only called once in the beginning of solving a QP probem and gives the following data:
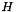describes the prox term given by the QPSolverProxObject,
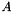is the matrix giving the linear constraints of the groundset
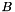describe the bundle with subgradient information given as rows in the QPModelBlockObject,
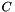describes the collected trace/penalty constraints of the models in QPModelBlockObject.
For forming each particular primal dual KKT system to be used in one predictor and mostly followed by one corrector solve, the routine QPinit_KKTsystem() and the model will provide positive (definite) barrier contributions. QPinit_KKTsystem() will be called at the beginning of each interior point iteration (before computing predictor and corrector step). The barrier contributions are represented here by
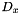(box constraints on variables, KKTdiagx in QPinit_KKTsystem()),
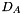(maybe box constraints on linear constraints 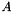unless 0 for equations, KKTdiagy in QPinit_KKTsystem()),
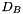(model variables obtained implicitly from the QPModelBlockObject),
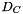(maybe slack variables on trace constraints of the model unless 0 for equations, obtained implicitly from the QPModelBlockObject).
Finally one predictor and one corrector call to QPsolve_KKTsystem() per interior point iteration asks to solve for the right hand side values
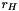"dual" right hand side (dualrhs in QPsolve_KKTsystem())
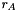"primal" right hand side of the ground set (primalrhs in QPsolve_KKTsystem())
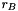"bundle" right hand side of the model (provided by QPModelBlockObject)
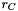and a model constraint right hand side (provided by QPModelBlockObject).
With these the primal dual KKT System of a QPKKTSolverObject reads
![\[ \left[\begin{array}{cccc} H + D_x & A^\top & B^\top & 0 \\ A & -D_A & 0 & 0 \\ B & 0 & -D_B & C \\ 0 & 0 & C & D_C \end{array} \right] \left(\begin{array}{c}x\\y\\ \xi \\ \zeta\end{array}\right) = \left(\begin{array}{c}r_H\\r_A\\ r_B \\r_C\end{array}\right) \]](form_158.png)
Correspondingly we will speak of the blocks H, A, B, C of the system.
Internally the QPKKTSolverObject may of course form variants via partial Schur complements and the like in order to best match the structural requirements of the model or application at hand.
One choice involves modelling the quadratic term H internally by a second order cone. Eliminating this part just results in using a scaled version of H. This is the Hfactor used in QPinit_KKTsystem(). Without the second order cone has value 1.
Some implemented examples are indicated in Internal QP Solver for linearly constrained groundsets.
Member Function Documentation
◆ QPinit_KKTdata()
|
pure virtual |
returns 1 if this class is not applicable in the current data situation, otherwise it stores the data pointers and these need to stay valid throught the use of the other routines but are not deleted here
- Parameters
-
Hp may not be be NULL model may be NULL A may be NULL eq_indices if not NULL these rows of A correspond to equations
Implemented in ConicBundle::QPKKTSolverComparison, ConicBundle::QPDirectKKTSolver, ConicBundle::QPIterativeKKTHAeqSolver, and ConicBundle::QPIterativeKKTSolver.
Referenced by QPKKTSolverObject().
The documentation for this class was generated from the following file:
