This text explains the theory and implementation of the example file "mc_triangle.cxx" whose source code is appended at the end. The text is structured as follows. It first introduces the max-cut problem and its canonical semidefinite relaxation and explains how this basic relaxation is implemented in the "main()" routine. Then it describes the Goemans-Williamson rounding procedure with its implementation in the subroutine "GW_rounding()". Finally the triangle inequalities are introduced and it is explained how they are added dynamically in the routine "update_triangle_constraints()".
Max-Cut and Semidefinite Relaxation
Given a graph 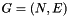 on node set s
on node set s 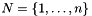 and edge set
and edge set 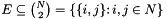 , the (unweighted) max-cut problem asks for a subset
, the (unweighted) max-cut problem asks for a subset 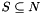 so that the cardinality
so that the cardinality 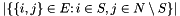 of the edges in the cut (running between
of the edges in the cut (running between 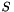 and
and 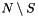 ) is maximized.
) is maximized.
For introducing the semidefinite relaxation we first need an algebraic formulation. Let the partition of nodes into 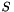 and
and 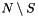 be represented by a vector
be represented by a vector 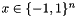 (it does not matter, whether 1 or -1 represents
(it does not matter, whether 1 or -1 represents 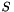 ). Then
). Then 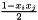 is 1 if
is 1 if 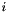 and
and 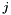 are on different sides and 0 otherwise. So, if
are on different sides and 0 otherwise. So, if 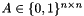 is the adjacency matrix with
is the adjacency matrix with 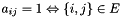 , the an algebraic formulation of Max-Cut is
, the an algebraic formulation of Max-Cut is
![\[ \mbox{(MC)}\quad \max_{x\in\{-1,1\}^n} \sum_{i<j}a_{ij}\frac{1-x_ix_j}2.\]](form_20.png)
This can be expressed in concise form with the graph Laplacian 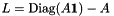 [it collects the sum of the edges (the degree) on the diagonal and is minus the adjacency matrix on the offdiagonal elements],
[it collects the sum of the edges (the degree) on the diagonal and is minus the adjacency matrix on the offdiagonal elements],
![\[ \mbox{(MC)}\quad\Leftrightarrow\quad \max_{x\in\{-1,1\}^n} \frac14x^\top L x\]](form_22.png)
The factor 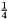 accounts for the
accounts for the 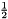 of the indicator term and the summing over both
of the indicator term and the summing over both 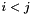 and
and 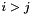 .
.
For the next step we need the inner product between matrices 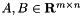 for arbitrary dimensions
for arbitrary dimensions 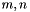 . We use the trace- or Frobenius inner product
. We use the trace- or Frobenius inner product ![$\langle A,B\rangle:=\mathrm{trace}(B^\top A)=\sum_i[A^\top B]_{ii}=\sum_{i,j} A_{ij}B_{ij}$](form_29.png) , then
, then
![\[ x^\top Lx=\langle Lx,x\rangle =\langle L,xx^\top\rangle. \]](form_30.png)
Observe that 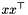 is a positive semidefinite matrix of rank one with all diagonal entries equal to one (because
is a positive semidefinite matrix of rank one with all diagonal entries equal to one (because 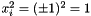 ). The canonical semidefinite relaxation of Poljak and Rendl is now obtained by relaxing
). The canonical semidefinite relaxation of Poljak and Rendl is now obtained by relaxing 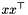 to a positive semidefinite matrix
to a positive semidefinite matrix 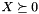 with all diagonal entries equal to one,
with all diagonal entries equal to one, 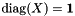 , while dropping the nonconvex rank one constraint,
, while dropping the nonconvex rank one constraint,
![\[ \mbox{(SMC)} \quad \begin{array}{ll} \max & \langle\frac14 L,X\rangle\\ \mbox{s.t.} & \mathrm{diag}(X)=\mathbf{1} \\ & X\succeq 0 \end{array} \]](form_35.png)
ConicBundle::PSCAffineFunction offers the support function (i.e., the supremum of a linear function over some set) 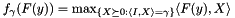 , where
, where 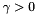 and
and 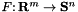 is an affine matrix function like
is an affine matrix function like 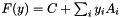 . To get (SMC) into this form, we may exploit that any feasible
. To get (SMC) into this form, we may exploit that any feasible 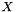 satisfies
satisfies 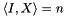 , but we need to introduce Lagrange multipliers to move the diagonal constraints into the cost function,
, but we need to introduce Lagrange multipliers to move the diagonal constraints into the cost function,
![\[ \mbox{(SMC)}\quad\Leftrightarrow\quad \min_{y\in\mathbf{R}^n} \max_{\{X\succeq 0\colon \langle I,X\rangle =n\}}[\langle\frac14 L-\sum_{i=1}^n y_iE_{ii},X\rangle +\mathbf{1}^\top y],\]](form_42.png)
where 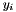 is the multiplier for the i-th diagonal constraint
is the multiplier for the i-th diagonal constraint 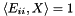 . The matrix
. The matrix 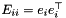 has a single one in diagonal entry
has a single one in diagonal entry 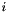 and is zero otherwise. As an aside, adding the trace constraint while keeping all diagonal constraints introduces redundancy and the dual solutions are not unique, but we do not worry about this here. The equivalence is otherwise guaranteed by standard semidefinite duality theory.
and is zero otherwise. As an aside, adding the trace constraint while keeping all diagonal constraints introduces redundancy and the dual solutions are not unique, but we do not worry about this here. The equivalence is otherwise guaranteed by standard semidefinite duality theory.
Implementing the Semidefinite Relaxation
With this we may now start to look at the routine "main()" in the source code of "mc_triangle.cxx" at the end of the text.
Reading the Graph Input Format
The first few lines read the graph description with nnodes and medges=  edges of the form
edges of the form  with (ignored) weight
with (ignored) weight 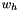 for
for 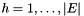 from standard input in the input format (as produced by the random graph generator rudy with indices starting at 1)
from standard input in the input format (as produced by the random graph generator rudy with indices starting at 1)
nnodes medges i_1 j_1 2_1 i_2 j_2 w_2 ... i_medges j_medges w_medges
For generating the sparse matrix representation of the Laplacian each of the index vectors to i (indi) and j (indj) is stored in a CH_Matrix_Classes::Indexmatrix, but in ConicBundle and in CH_Matrix_Classes indexing starts with 0, so each index is reduced by one. The uniform edge weight one is stored in the vector val of the same length and of type CH_Matrix_Classes::Matrix (replace this if you want general weights).
Generating 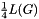 with averaged diagonal
with averaged diagonal
Next, in the code the CH_Matrix_Classes::Sparsesym L will almost hold the matrix 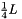 from above with the difference, that the final diagonal elements will all have the identical value
from above with the difference, that the final diagonal elements will all have the identical value 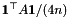 which seems to be a slightly better starting point in general. For this, L is first initialized by (nnodes,medges,indi,indj,val), the potential diagonal elements are deleted [it would be more efficient to ignore them on reading the input but this would complicate explanations], the sign of the offdiagonals is flipped and the averaged degree is added on the diagonal. Finally the factor
which seems to be a slightly better starting point in general. For this, L is first initialized by (nnodes,medges,indi,indj,val), the potential diagonal elements are deleted [it would be more efficient to ignore them on reading the input but this would complicate explanations], the sign of the offdiagonals is flipped and the averaged degree is added on the diagonal. Finally the factor 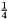 is applied. The solution vector bestcut (representing the best found
is applied. The solution vector bestcut (representing the best found 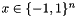 ) is initialized to the empty cut and the corresponding value is stored in bestcut_val.
) is initialized to the empty cut and the corresponding value is stored in bestcut_val.
Setting up the ConicBundle::PSCAffineFunction
In the next step the affine matrix function
![\[F(y)=C+\sum_{i=1}^m y_iA_i\quad \to \quad mc(y)=\frac14 L-\sum_{i=1}^n y_iE_{ii}\]](form_53.png)
is formed. In general a ConicBundle::PSCAffineFunction may have diagonal blocks of different orders and these sizes are communicated by a CH_Matrix_Classes::Indexmatrix Xdim (here there is only one block of order nnodes); the coefficients are specified by a ConicBundle::SparseCoeffmatMatrix C having only one column of the block diagonal form Xdim and a ConicBundle::SparseCoeffmatMatrix opAt with 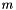 (here initially nnodes many) columns of block diagonal form Xdim. In the code Xdim signals one block of order nnodes, C is initialized to block structure Xdim and one column, its element (0,0) is then set to hold a coefficient matrix of type ConicBundle::CMsymsparse which is initialized to a copy of L. Likewise, opAt is initialized to diagonal block structure Xdim with nnodes columns, each element (0,i) is set to contain a coefficient matrix of type ConicBundle::CMsingleton holding
(here initially nnodes many) columns of block diagonal form Xdim. In the code Xdim signals one block of order nnodes, C is initialized to block structure Xdim and one column, its element (0,0) is then set to hold a coefficient matrix of type ConicBundle::CMsymsparse which is initialized to a copy of L. Likewise, opAt is initialized to diagonal block structure Xdim with nnodes columns, each element (0,i) is set to contain a coefficient matrix of type ConicBundle::CMsingleton holding 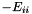 for i=1,..,nnodes. Now the PSCAffineFunction mc is initialized with C and opAt and, as last and optional argument, it is passed a ConicBundle::GramSparsePSCPrimal object initialized to contain the support of L. Passing this "Primal" instructs the code on what kind of primal information it should form / aggregate along with forming the aggregate subgradient. The internal solution of the semidefinite quadratic subproblem is of the form
for i=1,..,nnodes. Now the PSCAffineFunction mc is initialized with C and opAt and, as last and optional argument, it is passed a ConicBundle::GramSparsePSCPrimal object initialized to contain the support of L. Passing this "Primal" instructs the code on what kind of primal information it should form / aggregate along with forming the aggregate subgradient. The internal solution of the semidefinite quadratic subproblem is of the form 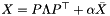 , where
, where 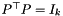 describes a face of the semidefinite cone of order k,
describes a face of the semidefinite cone of order k, 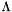 is a diagonal matrix and
is a diagonal matrix and 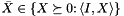 is an aggregate matrix so that
is an aggregate matrix so that 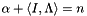 . The aggregate
. The aggregate 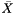 is not stored in full (for large orders this would not be efficient), but only on the support specified by the Primal, so here on the support of L. By the default bundle update rule the main information is kept in
is not stored in full (for large orders this would not be efficient), but only on the support specified by the Primal, so here on the support of L. By the default bundle update rule the main information is kept in 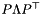 and the ConicBundle::GramSparsePSCPrimal instructs the code to return the matrix
and the ConicBundle::GramSparsePSCPrimal instructs the code to return the matrix 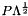 as the Gram part of the primal. This will be important for the triangle separation part. The final line of this code part sets the output options of mc to report only warnings and errors.
as the Gram part of the primal. This will be important for the triangle separation part. The final line of this code part sets the output options of mc to report only warnings and errors.
Initializing the Solver with Design Variables and Function
The next block initializes the bundle solver cbsolver and adds the function mc that is to be optimized. In ConicBundle::MatrixCBSolver::init_problem() the dimension of the design variables (here the initial number of 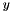 -variables is nnodes) is set with the lower and upper bounds lb and ub on these variables, no starting values, but linear cost coefficients in rhs (here the rhs vector is the
-variables is nnodes) is set with the lower and upper bounds lb and ub on these variables, no starting values, but linear cost coefficients in rhs (here the rhs vector is the 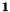 vector of the diagonal constraints) [instead of lb and ub one could just pass the NULL vector because they only give the default values]. Then the function mc is added with function factor
vector of the diagonal constraints) [instead of lb and ub one could just pass the NULL vector because they only give the default values]. Then the function mc is added with function factor 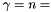 nnodes as an objective function, so that
nnodes as an objective function, so that 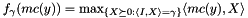 is the function optimized. Of the last two arguments in ConicBundle::MatrixCBSolver::add_function() the 0 informs the solver that there is no AffineFunctionTransformation, and the "true" tells the solver that the argument vector of the function will be adapted dynamically with any addition or deletion of design variables. This will again be important for the addition of triangle inequalities.
is the function optimized. Of the last two arguments in ConicBundle::MatrixCBSolver::add_function() the 0 informs the solver that there is no AffineFunctionTransformation, and the "true" tells the solver that the argument vector of the function will be adapted dynamically with any addition or deletion of design variables. This will again be important for the addition of triangle inequalities.
The Main Loop for Solving the Relaxation with Intermediate Interaction
If the optimization problem is not changed during runtime, a call to ConicBundle::MatrixCBSolver::solve() without arguments would suffice for solving the problem. Here, however, the point is to add further inequalities to (SMC) on the fly. As we solve the Lagrangian dual, the Lagrange multipliers to new inequalities are added as new design variables to the problem. In linear programming this would be done via call back routines, but in ConicBundle everything is designed to work with Lagrangian relaxation of inequalities that affect several otherwise unrelated convex functions a the same time. So typically call backs cannot be assigned to single functions but a global view of the problem is needed. Therefore ConicBundle offers a reverse interface by allowing to interrupt the algorithm after every descent step (safest variant) or even after every so many null steps for applying problem modifications. The draw back is that the user has to make sure that the selected dynamic problem modifications do not endanger convergence to the solution of the intended problem.
Before the main loop is started, some preparations are made for adding triangle inequalities like initializing the set of added triangle inequalities, their maximum violation observed. The call to ConicBundle::MatrixCBSolver::set_active_bounds_fixing() allows the solver to fix design variables at their bounds if they show no tendency to move away from the bounds. Here, for the nonnegative Lagrange multipliers of inequality constraints, this amounts to internally ignore inequalities whose multipliers stay at 0 in future QP subproblem as if they had not been added at all. This may speed up the subproblem solution considerably. A variable fixed at zero by this heuristic can be removed without problems afterwards.
The main loop itself starts with calling ConicBundle::MatrixCBSolver::solve() with the options to stop after at most 10 null steps as well as after each descent step. ConicBundle::MatrixCBSolver::get_approximate_primal() then retrieves the current approximate primal solution primalX in the representation selected in setting up the affine matrix function mc(). This primalX is then used in the GW_rounding() routine to generate a hopefully good partition for the max-cut problem. The best partition maximizing 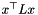 so far is returned in bestcut and its value is given in bestcut_val. Because all edge weights are set to one, optimality of bestcut_val is guaranteed if the gap between the bound returned by ConicBundle::MatrixCBSolver::get_objval() and bestcut_val is less than one, in which case the code exits the loop. Otherwise ConicBundle::MatrixCBSolver::get_fixed_active_bounds() retrieves the indices to Lagrange multipliers of inequalities that were fixed to zero by the internal heuristic and calls the routine update_triangle_constraints() for adding new violated triangle inequalities and deleting previously added inequalities that now seem irrelevant.
so far is returned in bestcut and its value is given in bestcut_val. Because all edge weights are set to one, optimality of bestcut_val is guaranteed if the gap between the bound returned by ConicBundle::MatrixCBSolver::get_objval() and bestcut_val is less than one, in which case the code exits the loop. Otherwise ConicBundle::MatrixCBSolver::get_fixed_active_bounds() retrieves the indices to Lagrange multipliers of inequalities that were fixed to zero by the internal heuristic and calls the routine update_triangle_constraints() for adding new violated triangle inequalities and deleting previously added inequalities that now seem irrelevant.
The main loop is terminated once no more sufficiently violated inequalities are found and no significant further progress is expected in the bound or if the last call to solve resulted in some error termination condition.
The "main()" routine ends with displaying the reason for termination.
This also ends the description of the "main()" routine, and the text next describes the rounding procedure "GW_rounding()" which will be followed by the description of the routine for dynamically adding and deleting triangle inequalities.
Goemans Williamson Random Hyperplane Rounding
The approximation algorithm of Goemans and Williamson for max-cut is based on random hyperplane rounding that can be applied to any feasible solution of (SMC). Let 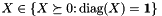 and factorize
and factorize 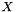 into
into 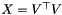 with
with ![$V=[v_1,\dots,v_n]$](form_71.png) . The
. The 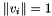 are unit vectors satisfying
are unit vectors satisfying 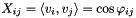 with
with 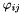 the angle between the two vectors. The larger the angle, the more likely i and j should end up in opposite partitions. A consistent way of doing so is achieved by picking a random hyperplane via choosing its normal vector
the angle between the two vectors. The larger the angle, the more likely i and j should end up in opposite partitions. A consistent way of doing so is achieved by picking a random hyperplane via choosing its normal vector 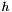 according to some spherically symmetric distribution, e.g. the multivariate standard normal distribution and setting
according to some spherically symmetric distribution, e.g. the multivariate standard normal distribution and setting
![\[ x_i=\left\{\begin{array}{rl} 1 & \mbox{if }\langle h,v_i \rangle > 0,\\ -1 & \mbox{if }\langle h,v_i \rangle \le 0.\\ \end{array}\right. \]](form_76.png)
For nonnegative edge weights the expected value of 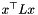 is then at least
is then at least 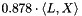 .
.
Implementation in GW_rounding()
In the routine GW_rounding() the input parameter primalX holds the available information on the current approximation to the primal matrix 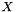 in the form conceived in the spectral bundle method of Helmberg and Rendl. I.e., one may think of the primal approximate solution as given in the form
in the form conceived in the spectral bundle method of Helmberg and Rendl. I.e., one may think of the primal approximate solution as given in the form 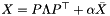 with
with 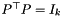 ,
, 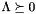 diagonal,
diagonal, 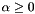 with
with 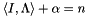 and an aggregate matrix
and an aggregate matrix 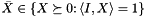 that is not available explicitly unless aggregated along on some support. The internal update rule for the orthonormal column vectors in
that is not available explicitly unless aggregated along on some support. The internal update rule for the orthonormal column vectors in 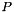 try to ensure that these capture the most important eigenspace of
try to ensure that these capture the most important eigenspace of 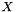 and
and 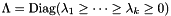 give the approximate sorted eigenvalues of
give the approximate sorted eigenvalues of 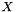 . The default update rule tries to ensure that
. The default update rule tries to ensure that 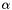 is small enough so that
is small enough so that 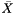 is not of relevance here.
is not of relevance here.
In the code the call to ConicBundle::GramSparsePSCPrimal::get_grammatrix() for primalX (which was obtained via ConicBundle::MatrixCBSolver::get_approximate_primal()) returns 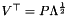 in the matrix Gram_mat, so the first column of Gram_mat actually holds the most important information about the current
in the matrix Gram_mat, so the first column of Gram_mat actually holds the most important information about the current 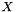 .
.
The first code block uses the signs of the first column of Gram_mat to produce a partition vector cut 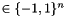 and evaluates it for the cost matrix L. If the result is better then the best partition vector found so far, it is stored as the new best partition.
and evaluates it for the cost matrix L. If the result is better then the best partition vector found so far, it is stored as the new best partition.
The second block actually uses Goemans Williamson random hyperplane rounding. It fixes a number of tries (the maximum of nnodes/10 and 10). The loop executes these tries by drawing a random direction (the normal vector 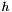 of above) according to the multivariate normal distribution into rand_dir. genmult computes Gram_mat*rand_dir into cut, so cut(i) holds the inner product of rand_dir with row i of Gram_mat, which corresponds to the value
of above) according to the multivariate normal distribution into rand_dir. genmult computes Gram_mat*rand_dir into cut, so cut(i) holds the inner product of rand_dir with row i of Gram_mat, which corresponds to the value 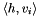 above. Then the signs of cut are used to generate the partition vector cut
above. Then the signs of cut are used to generate the partition vector cut 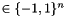 , which is again evaluated and compared.
, which is again evaluated and compared.
The final line of the routine outputs the current best value known.
It should be noted that a practical implementation might well try to use some local improvement heuristics on the outcomes of the random rounding procedure but this seems inappropriate for this tutorial.
Dynamic Addition and Deletion of Triangle Inequalities
The elliptope, i.e., the primal feasible set 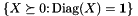 of (SMC), is a convex relaxation (a blown up version) of the matric cut polytope
of (SMC), is a convex relaxation (a blown up version) of the matric cut polytope 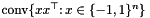 , see the book by Deza and Laurent for a full account of polyhedral theory related to the cut polytope and its variants and for further references. The most basic facet defining inequalities of the matric cut polytope are the so called triangle inequalities
, see the book by Deza and Laurent for a full account of polyhedral theory related to the cut polytope and its variants and for further references. The most basic facet defining inequalities of the matric cut polytope are the so called triangle inequalities
![\[ \begin{array}{cccccccl} &X_{ij}&+& X_{ik}&+&X_{jk}&\ge & -1,\\ &X_{ij}&-& X_{ik}&-&X_{jk}&\ge & -1,\\ - &X_{ij}&+& X_{ik}&-&X_{jk}&\ge & -1,\\ - &X_{ij}&-& X_{ik}&+&X_{jk}&\ge & -1. \end{array} \]](form_92.png)
Combinatorially they reflect that in a triangle graph on nodes i,j,k at most two of the edges ij, ik, jk can be in any cut and if there is one edge in the cut then another one must be in the cut as well.
In fact, for any cycle of the graph a cut always intersects an even number of the cycle's edges. The corresponding cycle inequalities can be separated in polynomial time. In linear programming approaches, these cycle inequalities form the basis of most relaxations. The cycle inequalities provide a complete description of the cut polytope of planar graphs. If all triangle inequalities are satisfied, all cycle inequalities are satisfied as well. In linear programming relaxations adding triangle inequalities for edges that are not in the support of the cost matrix does not help. In the semidefinite relaxation, however, even triangle inequalities outside the support may improve the value of the relaxation, because the semidefiniteness condition leads to nonlinear crossconnections between all matrix elements. For large sparse graphs it may be computationally too expensive to work work with the full matrix 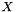 and separating the sparse cycle inequalities on a carefully selected support may improve running times considerably without a big loss in quality (see the work of Armbruster, Fuegenschuh, Helmberg and Martin). This, however, is clearly outside the scope of this tutorial implementation. So here, for the sake of simplicity, we will not worry about forming and using the dense
and separating the sparse cycle inequalities on a carefully selected support may improve running times considerably without a big loss in quality (see the work of Armbruster, Fuegenschuh, Helmberg and Martin). This, however, is clearly outside the scope of this tutorial implementation. So here, for the sake of simplicity, we will not worry about forming and using the dense 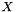 for full separation of the triangle inequalities by direct enumeration. Yet, forming the full matrix here is the sole reason why this example implementation is not a viable option for large scale sparse instances.
for full separation of the triangle inequalities by direct enumeration. Yet, forming the full matrix here is the sole reason why this example implementation is not a viable option for large scale sparse instances.
Suppose now that for some index set 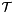 the triangle inequalities (multiplied by -1)
the triangle inequalities (multiplied by -1) 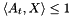 are added to (SMC), then
are added to (SMC), then
![\[ \mbox{(SMC)} \quad \begin{array}{ll} \max & \langle\frac14 L,X\rangle\\ \mbox{s.t.} & \mathrm{diag}(X)=\mathbf{1}, \\ & \langle A_t,X\rangle \le 1, \quad t\in\mathcal{T},\\ & X\succeq 0 \end{array} \quad\Leftrightarrow\quad \min_{y\in\mathbf{R}^{n+|\mathcal{T}|},y_{\mathcal{T}}\ge 0} \max_{\{X\succeq 0\colon \langle I,X\rangle =n\}}[\langle\frac14 L-\sum_{i=1}^n y_iE_{ii}-\sum_{t\in \mathcal{T}} y_tA_{t},X\rangle +\mathbf{1}^\top y] \]](form_95.png)
Thus, adding these primal inequalities corresponds to appending variables 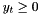 for
for 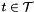 and appending the coefficient matrices
and appending the coefficient matrices 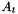 to the affine matrix function.
to the affine matrix function.
A central difference of the Lagrangian relaxation approach to standard linear programming implementations is that an approximate primal solution 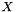 will only roughly satisfy newly added inequalities. Because Lagrange multipliers only penalize violations but do not prohibit violations, most added cutting planes will actually still be violated by the approximate primal solutions generated by the bundle method. So the same inequalities may be separated and added over and over again unless precautions are taken against that. It can be shown that it suffices to add the most violated cutting planes whenever they are not already present in the model in order to guarantee convergence. The implementation will therefore keep identifiers of the added triangle inequalities in a separate set, add violated inequalities only if their identifiers are not yet in the set, and delete inactive inequalities only after this test.
will only roughly satisfy newly added inequalities. Because Lagrange multipliers only penalize violations but do not prohibit violations, most added cutting planes will actually still be violated by the approximate primal solutions generated by the bundle method. So the same inequalities may be separated and added over and over again unless precautions are taken against that. It can be shown that it suffices to add the most violated cutting planes whenever they are not already present in the model in order to guarantee convergence. The implementation will therefore keep identifiers of the added triangle inequalities in a separate set, add violated inequalities only if their identifiers are not yet in the set, and delete inactive inequalities only after this test.
Implementation in update_triangle_constraints()
The routine consists of a small initial block for 0. forming the approximate primal X matrix and four successive blocks for 1. finding the most violated triangle inequalities, 2. building the coefficient matrices for those that are not yet included in the set of added triangle inequalities, 3. adding the new variables and coefficient matrices to the problem, and 4. deleting old inequalities whose multipliers have been fixed to zero in the heuristic for active bounds fixing.
0. Forming the Approximate Primal X Matrix
As described before, the input parameter primalX, retrieved by ConicBundle::MatrixCBSolver::get_approximate_primal() in the main loop, holds the available information on the current approximation to the primal matrix 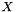 in the form conceived in the spectral bundle method of Helmberg and Rendl. I.e., internally the primal approximate solution is given in the form
in the form conceived in the spectral bundle method of Helmberg and Rendl. I.e., internally the primal approximate solution is given in the form 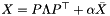 with
with 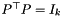 ,
, 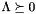 diagonal,
diagonal, 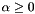 with
with 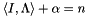 and an aggregate matrix
and an aggregate matrix 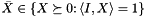 that is not available explicitly unless aggregated along on some support. The internal update rule for the orthonormal column vectors in
that is not available explicitly unless aggregated along on some support. The internal update rule for the orthonormal column vectors in 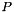 try to ensure that these capture the most important eigenspace of
try to ensure that these capture the most important eigenspace of 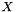 and
and 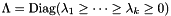 give the approximate sorted eigenvalues of
give the approximate sorted eigenvalues of 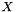 . Even though the default update rule tries to ensure that
. Even though the default update rule tries to ensure that 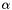 is small, it might be important for separation to have
is small, it might be important for separation to have 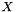 available on the original support of
available on the original support of 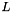 as precisely as possible. For this purpose the support of
as precisely as possible. For this purpose the support of 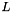 was entered in setting up the generating primal information when initializing the affine matrix function mc() in the routine main(). Due to this, any aggregation leading to the conceptual
was entered in setting up the generating primal information when initializing the affine matrix function mc() in the routine main(). Due to this, any aggregation leading to the conceptual 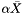 is carried out explicitly on the support of
is carried out explicitly on the support of 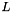 and available only on this support as CH_Matrix_Classes::Sparseym in the sparse symmetric matrix part of the class ConicBundle::GramSparsePSCPrimal, while the Gram matrix part retrievable by the call to ConicBundle::GramSparsePSCPrimal::get_grammatrix() returns
and available only on this support as CH_Matrix_Classes::Sparseym in the sparse symmetric matrix part of the class ConicBundle::GramSparsePSCPrimal, while the Gram matrix part retrievable by the call to ConicBundle::GramSparsePSCPrimal::get_grammatrix() returns 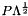 . So if
. So if 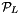 denotes the projection onto the support of
denotes the projection onto the support of 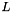 , primalX holds
, primalX holds 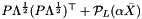 .
.
With the initialization "Symmatrix X(*primalX);" the variable X is initialized as a dense symmetric matrix with sparse symmetric matrix part 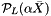 stored in primalX. The second line "rankadd(primalX->get_grammatrix(),X,1.,1.);" adds
stored in primalX. The second line "rankadd(primalX->get_grammatrix(),X,1.,1.);" adds 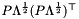 to X.
to X.
1. Finding the Most Violated Triangle Inequalities
For organizational purposes triangle inequalities are identified by the index triple 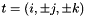 as implemented in the class Triangle which is equipped with a total order operator< for comparisons in the standard template library implementation std::set<Triangle> underlying the type AddedTriangles. The input/output parameter added_triangles holds the set of triangle inequalities
as implemented in the class Triangle which is equipped with a total order operator< for comparisons in the standard template library implementation std::set<Triangle> underlying the type AddedTriangles. The input/output parameter added_triangles holds the set of triangle inequalities 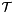 added to the problem. For identifying the most violated inequalities the class TriangleViolation stores a Triangle identifier together with the "violation value"
added to the problem. For identifying the most violated inequalities the class TriangleViolation stores a Triangle identifier together with the "violation value" 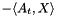 and offers a operator< so that the least violated inequalities (largest value
and offers a operator< so that the least violated inequalities (largest value 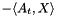 ) come first in the standard template library implementation std::priority_queue<TriangleViolation> most_violated.
) come first in the standard template library implementation std::priority_queue<TriangleViolation> most_violated.
The block starts with fixing an upper bound at_most_n_violated on the number of violated triangle inequalities to be added in this call and a threshold on the "violation value" 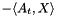 (everything below -1 is violated, so the value -1-1e-3 corresponds to an actual minimum violations of 1e-3).
(everything below -1 is violated, so the value -1-1e-3 corresponds to an actual minimum violations of 1e-3).
The three loops enumerate all possible triangles. A inequality violated according to the threshold is added to the priority queue if there is still room or if it is more violated then the least violated one of the queue, which is then popped followed by insertion of the new inequality.
2. Building the Coefficient Matrices
For later initialization of the ConicBundle::SparseCoeffmatMatrix that needs to be appended to mc(), it will be convenient to collect the coefficient matrices of new triangles inequalities in the ConicBundle::CoeffmatVector tr_ineqs which is simply a std::vector of ConicBundle::CoeffmatPointer (pointers to coefficient matrices). For each triangle inequality the appropriate format of a coefficient matrix is a ConicBundle::CMsymsparse which needs to be initialized via sparse symmetric matrix CH_Matrix_Classes::Sparsesym A, which will have the three nonzero elements corresponding to the pairs ij, ik, jk. The corresponding vectors describing the indices and values of A are initialized to the appropriate sizes before entering the loop on the violated triangle inequalities.
The loop continues as long as the priority queue most_violated still holds entries. The top element is checked on containment in the set added_triangles and skipped if it is in there. Otherwise its tree violation is computed for displaying some statistical information, it is added into added_triangles, and a new coefficient matrix formed via the Sparsesym A is appended to tr_ineqs.
Note that it may happen that all separated inequalities are already in the set added_triangles because a few iterations of the bundle method may not suffice to reduce violation sufficiently for other inequalities to emerge. In this case the reported violation is 0 and may not reflect to correct state of things.
3. Adding the New Variables and Coefficient Matrices
When appending new variables via MatrixCBSolver::append_variables() it is also necessary to communicate to the function mc() how to modify itself via specifying in the function object modification map ConicBundle::FunObjModMap modmap a corresponding ConicBundle::PSCAffineModification object funmod for the function mc(). For performing consistency checks all modification objects have to be initialized with the current dimensions of the object to be modified; after that, modifications can be added consistently to the modification object which collects them for later collective application to the intended object. Here a ConicBundle::SparseCoeffmatMatrix scm holding as columns the new coefficient matrices collected in tr_ineqs is appended to funmod in a call to its routine ConicBundle::PSCAffineModification::add_append_vars(). The reference to funmod is then entered into the modification map modmap for mc(). In the call to ConicBundle::MatrixCBSolver::append_variables() this modification map modmap is then passed along with the number of variables to be appended, their lower bounds (value 0 for nonnegative), upper bounds (Null pointer for not existing), two null pointers for constraint columns and starting values, and the cost vector of all ones.
Note that in adding new inequalities 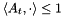 whose support is outside
whose support is outside 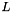 the corresponding subgradient entry
the corresponding subgradient entry 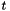 cannot be recovered for the aggregate
cannot be recovered for the aggregate 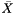 , because the precise values of some entries of
, because the precise values of some entries of 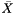 needed in the evaluation of
needed in the evaluation of 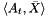 are not available. So whenever such inequalities are added, the aggregate will automatically be removed from the cutting model of the bundle method. This may lead to a noticeable loss in the quality of the cutting model whenever the corresponding coefficient
are not available. So whenever such inequalities are added, the aggregate will automatically be removed from the cutting model of the bundle method. This may lead to a noticeable loss in the quality of the cutting model whenever the corresponding coefficient 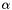 is sizable. This is another reason in favor of bundle updating rules that keep
is sizable. This is another reason in favor of bundle updating rules that keep 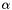 small as well as in favor of separating inequalities on the updated support of
small as well as in favor of separating inequalities on the updated support of 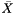 .
.
4. Deleting old inequalities
In deleting inequalities and their associated Lagrange multipliers it is convenient if the current function evaluations and cutting models stay valid. The cutting model is generated by a subset of 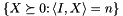 and the latter is not affected by deletions of coordinates in existing subgradients, so the cutting model is not affected in any way by deletions. For function evaluations the matter is more delicate. Here the objective is a support function evaluated for a cost vector affinely depending on the design variables y. For such functions any deletion of variables of value zero does not affect the outcome. Therefore deleting variables that are exactly zero in the current center and the current candidate (they coincide after descent steps) is safe. If, however, the deleted variable has a value ever so slightly deviating from zero, ConicBundle will automatically reevaluate the function at the respective point. In order to be sure that problem modifications do not cause additional evaluations it is convenient to use the heuristic enabled by ConicBundle::MatrixCBSolver::set_active_bounds_fixing() in main(). If the current center has a variable at its bounds and for a candidate the same bound is strongly active for the same variable, this variable is fixed to this bound for the next iterations until a descent step occurs. If, after the descent step, the variable is not deleted, it is set free again (and maybe fixed anew directly afterwards).
and the latter is not affected by deletions of coordinates in existing subgradients, so the cutting model is not affected in any way by deletions. For function evaluations the matter is more delicate. Here the objective is a support function evaluated for a cost vector affinely depending on the design variables y. For such functions any deletion of variables of value zero does not affect the outcome. Therefore deleting variables that are exactly zero in the current center and the current candidate (they coincide after descent steps) is safe. If, however, the deleted variable has a value ever so slightly deviating from zero, ConicBundle will automatically reevaluate the function at the respective point. In order to be sure that problem modifications do not cause additional evaluations it is convenient to use the heuristic enabled by ConicBundle::MatrixCBSolver::set_active_bounds_fixing() in main(). If the current center has a variable at its bounds and for a candidate the same bound is strongly active for the same variable, this variable is fixed to this bound for the next iterations until a descent step occurs. If, after the descent step, the variable is not deleted, it is set free again (and maybe fixed anew directly afterwards).
Here the only bounds are the lower bounds zero and any variable fixed to this bound by the heuristic will be exactly zero for the candidate as well. If the multiplier of a new inequality does not even start to get positive, its center coordinate still has value zero and so this quickly helps to get rid of less relevant inequalities. If multipliers got positive initially for some center point but then turned zero again, they may get fixed for this new center so that they are only deleted if their usefulness is in doubt repeatedly. The heuristic seems to work well but it is also not more than a rather simple heuristic.
The input variable fixed_indices provides a pointer to the indicator vector of fixed variable indices, if such a pointer was returned by the call to ConicBundle::MatrixCBSolver::get_fixed_active_bounds() in the main loop of main(). The variables to indices with nonzero entries in this vector are save to delete.
For didactic purposes rather than out of necessity each nonzero index is first tested for indeed having value zero in the center point centery retrieved by ConicBundle::MatrixCBSolver::get_center() before it is appended to the Indexmatrix delind. For each index in delind the corresponding coefficient matrix is extracted from mc() and cast into a pointer to ConicBundle::CMsymsparse. The sparse representation indi,indj,val obtained by calling ConicBundle::CMsymsparse::sparse() is then used to form the corresponding Triangle indicator t for finding and deleting t in the set added_triangles.
Finally the call to ConicBundle::MatrixCBSolver::delete_variables() with argument delind internally generates or updates the necessary modification objects that will be passed to the bundle method and the function mc() for actually deleting these indices and their associated bounds and coefficient matrices. The assignment of the new indices after deletion to the old indices before deletion is returned in map_to_old but this map is not needed here.
The deletion of variables is executed at the end of the function update_triangle_constraints() on purpose for two reasons. First, it seems pointless to add violated inequalities whose multipliers did not turn positive before even if the inequalities are still violated, so they should sill be present in added_triangles when testing for the addition of new inequalities. Second, when retrieving data after some variables have been deleted, the accumulated modifications on the problem description are executed first before returning the data. This may cause unnecessary additional work and even difficulties if some data like function values is invalidated by these modifications.
 1.8.13
1.8.13