Next: The ansatz
Up: Notation, the NDFT and
Previous: Inverse NDFT
For clarity of presentation the ideas behind the NFFT will be shown for the case 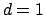 and the algorithm ndft.
The generalisation of the FFT is an approximative algorithm and has computational complexity
and the algorithm ndft.
The generalisation of the FFT is an approximative algorithm and has computational complexity
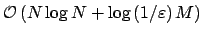 , where
, where
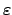 denotes the desired accuracy.
The main idea is to use standard FFTs and a window function
denotes the desired accuracy.
The main idea is to use standard FFTs and a window function 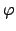 which is well localised in the
time/spatial domain
which is well localised in the
time/spatial domain
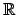 and in the frequency domain
and in the frequency domain
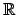 . Several window functions were proposed,
see [5,2,22,9,8].
. Several window functions were proposed,
see [5,2,22,9,8].
The considered problem is the fast evaluation of
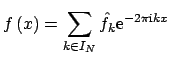 |
(2.6) |
at arbitrary knots
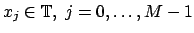 .
.
Subsections
Stefan Kunis
2004-09-03