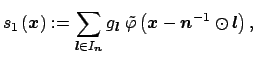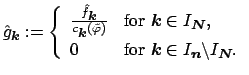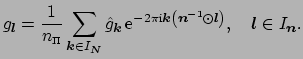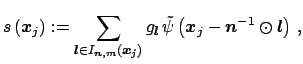The case $d>1$

Starting with the original problem of evaluating the multivariate trigonometric polynomial in (2.1) one has to do a few generalisations. The window function is given by

$$\varphi\left(\mbox{\boldmath {${x}$}}\right):=\varphi_0\left(x_0\right) \varphi_1\left(x_1\right) \hdots \varphi_{d-1}\left(x_{d-1}\right)$$

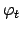where $\varphi_t$ is an univariate window function. Thus, a simple consequence is

$$c_{\mbox{\boldmath\scriptsize {${k}$}}}\left(\tilde \varphi\right... ...ft(\tilde \varphi_1\right) \hdots c_{k_{d-1}}\left(\tilde \varphi_{d-1}\right).$$

The ansatz is generalised to

$$s_1\left(\mbox{\boldmath {${x}$}}\right) := \sum_{\mbox{\boldmath... ...h {${x}$}} - \mbox{\boldmath {${n}$}}^{-1}\odot\mbox{\boldmath {${l}$}}\right),$$

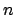
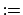
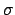
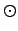
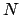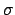
where the fft-size is given by ${n}$$:=$${\sigma}$$\odot$   ${N}$ and the oversampling factors by 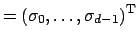${\sigma}$$=\left(\sigma_0,\hdots,\sigma_{d-1}\right)^{\rm T}$. Along the lines of (2.10) one defines

$$\hat g_{\mbox{\boldmath\scriptsize {${k}$}}} := \left\{ \begin{a... ... \backslash I_{\mbox{\boldmath\scriptsize {${N}$}}} . \\ \end{array} \right.$$

The values 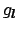$g_{\mbox{\boldmath\scriptsize {${l}$}}}$ can be obtained by a (multivariate) FFT of size 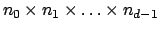$n_0 \times n_1 \times \hdots \times n_{d-1}$ as

$$g_{\mbox{\boldmath\scriptsize {${l}$}}} = \frac{1}{n_{\text{\tiny... ..., \quad \mbox{\boldmath {${l}$}} \in I_{\mbox{\boldmath\scriptsize {${n}$}}}.$$

Using the compactly supported function $\psi\left(\mbox{\boldmath {${x}$}}\right)=\varphi\left(\mbox{\boldmath {${x}$}}\right)\chi_{[-{m \over n},{m \over n}]^d}\left(\mbox{\boldmath {${x}$}}\right)$, one obtains

$$s\left(\mbox{\boldmath {${x}$}}_j\right) := \sum_{\mbox{\boldmath... ...}$}}_j - \mbox{\boldmath {${n}$}}^{-1}\odot\mbox{\boldmath {${l}$}}\right) \, ,$$

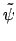where $\tilde \psi$ again denotes the one periodic version of 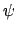$\psi$ and the multi index set is given by

$$I_{\mbox{\boldmath\scriptsize {${n}$}},m} \left(\mbox{\boldmath {... ...{n}$}} \odot \mbox{\boldmath {${x}$}}_j + m \mbox{\boldmath {${1}$}}\right\}\,.$$