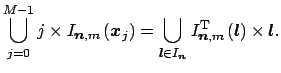Next: Window functions
Up: NFFT
Previous: The case
In summary, the following Algorithm 1 is obtained for the fast computation of
(2.2) with
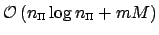 arithmetic operations.
arithmetic operations.
![\begin{algorithm}
% latex2html id marker 529
[ht]
\caption{\tt NFFT
}
Input:...
...gorithmic}
Output: approximate values $f_j,\;j=0,\hdots,M-1$.
\end{algorithm}](img175.png)
Algorithm 1 reads in matrix vector notation as
where
 denotes the real
denotes the real
 sparse matrix
sparse matrix
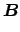 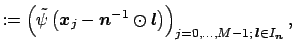 |
(2.12) |
where
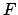 is the Fourier matrix of size
is the Fourier matrix of size
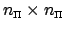 ,
and where
,
and where
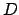 is the real
is the real
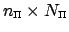 'diagonal' matrix
'diagonal' matrix
with zero matrices
 of size
of size
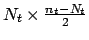 .
.
The corresponding computation of the adjoint matrix vector product reads as
With the help of the transposed index set
one obtains Algorithm 2 for the adjoint nfft.
![\begin{algorithm}
% latex2html id marker 596
[htbp]
\caption{\tt NFFT$^{\rm H}...
...boldmath {${k}$}} \in I_{\mbox{\boldmath\scriptsize {${N}$}}}$.
\end{algorithm}](img193.png)
Due to the characterisation of the non zero elements of the matrix
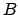 , i.e.,
, i.e.,
the multiplication with the sparse matrix
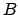
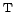 is implemented in a 'transposed' way in the library,
summation as outer loop and only using the multi index sets
is implemented in a 'transposed' way in the library,
summation as outer loop and only using the multi index sets
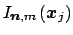 .
.



Next: Window functions
Up: NFFT
Previous: The case
Stefan Kunis
2004-09-03
![\begin{algorithm}
% latex2html id marker 529
[ht]
\caption{\tt NFFT
}
Input:...
...gorithmic}
Output: approximate values $f_j,\;j=0,\hdots,M-1$.
\end{algorithm}](img175.png)
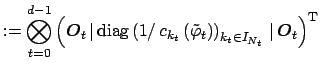
![\begin{algorithm}
% latex2html id marker 596
[htbp]
\caption{\tt NFFT$^{\rm H}...
...boldmath {${k}$}} \in I_{\mbox{\boldmath\scriptsize {${N}$}}}$.
\end{algorithm}](img193.png)