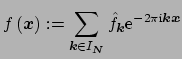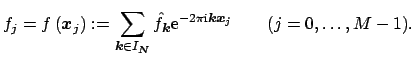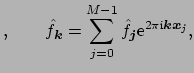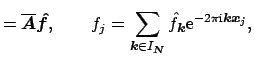Next: Equispaced knots
Up: NDFT
Previous: NDFT
The first problem to be adressed can be regarded as a matrix vector multiplication. For a finite number of
given Fourier coefficients
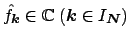 one wants to evaluate the trigonometric polynomial
one wants to evaluate the trigonometric polynomial
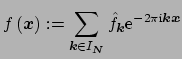 |
(2.1) |
at given non equispaced knots
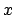
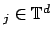 .
Thus, our concern is the evaluation of
.
Thus, our concern is the evaluation of
In matrix vector notation this reads as
where
As already mentioned, all 'vec'-operation are omitted, and the matrix vector product is defined by
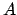
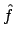
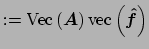 .
The straight forward algorithm of this matrix vector product, which is called ndft, takes
.
The straight forward algorithm of this matrix vector product, which is called ndft, takes
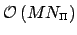 arithmetical operations.
arithmetical operations.
Related matrix vector products are the adjoint ndft
the conjugated ndft
and the transposed ndft
where
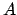
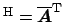 .
.



Next: Equispaced knots
Up: NDFT
Previous: NDFT
Stefan Kunis
2004-09-03