


Next: Inverse NDFT
Up: NDFT
Previous: Direct NDFT
For
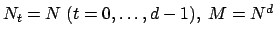 and equispaced knots
and equispaced knots
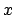
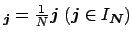 the computation of
(2.2) is known as (multivariate) discrete Fourier transform (DFT). In this special case,
the input data
the computation of
(2.2) is known as (multivariate) discrete Fourier transform (DFT). In this special case,
the input data
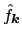 are called discrete Fourier coefficients and the samples
are called discrete Fourier coefficients and the samples
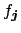 can be computed by the well known fast Fourier transform (FFT) with only
can be computed by the well known fast Fourier transform (FFT) with only
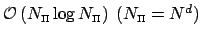 arithmetic operations. Furthermore, one has an inversion formula
arithmetic operations. Furthermore, one has an inversion formula
which does NOT hold true for the non equispaced case in general.
Stefan Kunis
2004-09-03