


Next: NFFT
Up: NDFT
Previous: Equispaced knots
In general there is no simple inversion formula, hence one deals with the following reconstruction or recovery problem.
Given the values
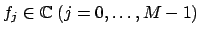 at non equispaced knots
at non equispaced knots
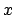
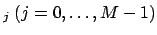 , the aim
is to reconstruct a trigonometric polynomial
, the aim
is to reconstruct a trigonometric polynomial 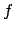 resp. its Fourier-coefficients
resp. its Fourier-coefficients
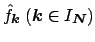 with
with
Often, the number of nodes 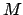 and the dimension of the space of the polynomials
and the dimension of the space of the polynomials
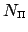 do not coincide, i.e., the matrix
do not coincide, i.e., the matrix
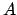 is rectangular. A standard
method is to use the Moore-Penrose-pseudoinverse solution
is rectangular. A standard
method is to use the Moore-Penrose-pseudoinverse solution
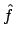
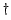 which solves the general linear least squares problem, see e.g.
[3, p. 15],
which solves the general linear least squares problem, see e.g.
[3, p. 15],
Of course, computing the pseudoinverse by the singular value decomposition is
very expensive here and no practical way at all.
For a comparative low polynomial degree
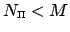 the linear
system
the linear
system
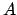
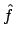
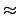
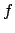 is over-determined, so that in general
the given data
is over-determined, so that in general
the given data
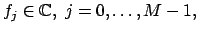 will be only approximated
up to the residual
will be only approximated
up to the residual
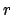
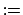
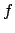
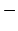
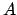
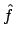 . One considers the
weighted approximation problem
. One considers the
weighted approximation problem
which may incorporate weights 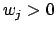 ,
,
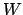
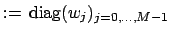 ,
to compensate for clusters in the sampling set
,
to compensate for clusters in the sampling set 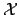 .
This problem is equivalent to the weighted normal equation of first kind
.
This problem is equivalent to the weighted normal equation of first kind
For a comparative high polynomial degree
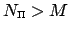 one expects to interpolate the
given data
one expects to interpolate the
given data
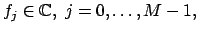 exactly. The (consistent)
linear system
exactly. The (consistent)
linear system
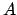
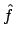
 is under-determined. One considers the
damped minimisation problem
is under-determined. One considers the
damped minimisation problem
which may incorporate 'damping factors'
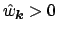 ,
,
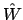
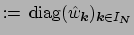 . A smooth solution is favoured, i.e.,
a decay of the Fourier coefficients
. A smooth solution is favoured, i.e.,
a decay of the Fourier coefficients
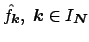 , for
decaying damping factors
, for
decaying damping factors
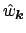 . This problem is equivalent to the
damped normal equation of second kind
. This problem is equivalent to the
damped normal equation of second kind



Next: NFFT
Up: NDFT
Previous: Equispaced knots
Stefan Kunis
2004-09-03
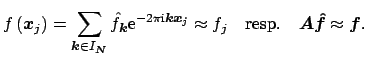
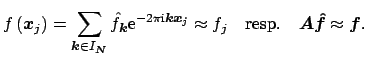
![]() the linear
system
the linear
system
![]()
![]()
![]()
![]() is over-determined, so that in general
the given data
is over-determined, so that in general
the given data
![]() will be only approximated
up to the residual
will be only approximated
up to the residual
![]()
![]()
![]()
![]()
![]()
![]() . One considers the
weighted approximation problem
. One considers the
weighted approximation problem
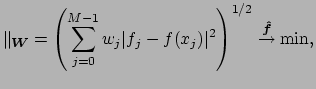
![]() one expects to interpolate the
given data
one expects to interpolate the
given data
![]() exactly. The (consistent)
linear system
exactly. The (consistent)
linear system
![]()
![]()
![]()
![]() is under-determined. One considers the
damped minimisation problem
is under-determined. One considers the
damped minimisation problem