


Next: Direct NDFT
Up: Notation, the NDFT and
Previous: Notation, the NDFT and
Let the torus
of dimension 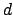 be given. It will serve as domain where the non equispaced knots
be given. It will serve as domain where the non equispaced knots
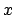 are taken from.
Thus, the sampling set is given by
are taken from.
Thus, the sampling set is given by
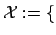
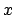
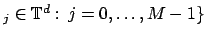 .
.
The space of all (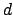 -variate, one-periodic) functions
-variate, one-periodic) functions
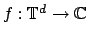 is restricted
to the space of
is restricted
to the space of 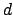 -variate trigonometric polynomials
-variate trigonometric polynomials
with degree
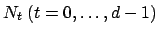 in the
in the 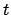 -th dimension. Possible frequencies
-th dimension. Possible frequencies
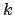 are
collected in the multi index set
are
collected in the multi index set
where
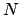
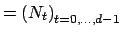 is the multi bandlimit. The dimension of
the space of
is the multi bandlimit. The dimension of
the space of 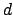 -variate trigonometric polynomials is given by
-variate trigonometric polynomials is given by
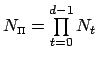 .
.
The inner product between the frequency
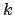 and the time/spatial knot
and the time/spatial knot
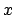 is defined in the usual way by
is defined in the usual way by
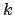
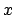
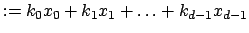 .
Furthermore, two vectors may be linked by the pointwise product
.
Furthermore, two vectors may be linked by the pointwise product
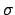
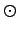
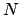
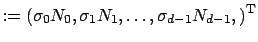 with its
inverse
with its
inverse
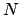
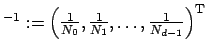 .
.
For clarity of presentation the multiindex
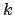 adresses elements of vectors and matrices as well, i.e.,
the plain index
adresses elements of vectors and matrices as well, i.e.,
the plain index
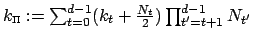 is not used here.
is not used here.
Subsections



Next: Direct NDFT
Up: Notation, the NDFT and
Previous: Notation, the NDFT and
Stefan Kunis
2004-09-03
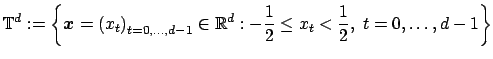
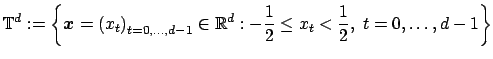
![]() -variate, one-periodic) functions
-variate, one-periodic) functions
![]() is restricted
to the space of
is restricted
to the space of ![]() -variate trigonometric polynomials
-variate trigonometric polynomials
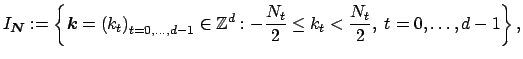
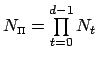 .
.
![]() and the time/spatial knot
and the time/spatial knot
![]() is defined in the usual way by
is defined in the usual way by
![]()
![]()
![]() .
Furthermore, two vectors may be linked by the pointwise product
.
Furthermore, two vectors may be linked by the pointwise product
![]()
![]()
![]()
![]() with its
inverse
with its
inverse
![]()
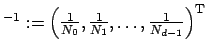 .
.
![]() adresses elements of vectors and matrices as well, i.e.,
the plain index
adresses elements of vectors and matrices as well, i.e.,
the plain index
![]() is not used here.
is not used here.