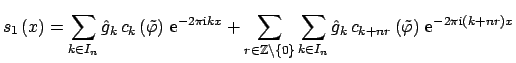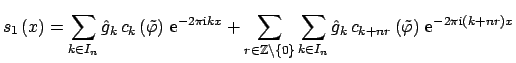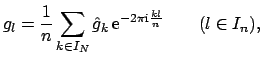next up previous
Next: The second approximation - Up: NFFT Previous: The window function

The first approximation - cutting off in frequency domain

Switching from the definition (2.7) to the frequency domain, one obtains

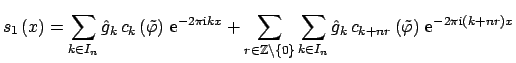$\displaystyle s_1\left(x\right) =\sum_{k \in I_n} \hat g_k \, c_k\left(\tilde... ...(\tilde \varphi\right) \, {\rm e}^{-2\pi{\mbox{\scriptsize {i}}} (k + n r)x }$ (2.8)

with the discrete Fourier coefficients

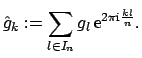$\displaystyle \hat g_k := \sum_{l \in I_n} g_l \, {\rm e}^{ 2\pi{\mbox{\scriptsize {i}}} \frac{k l}{n}}.$ (2.9)

Comparing (2.6) to (2.7) and assuming 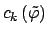$ c_k\left(\tilde\varphi\right)$ small for 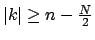$ \vert k\vert\ge n-\frac{N}{2}$ suggests to set

$\displaystyle \hat g_k := \left\{ \begin{array}{ll} \frac{\hat f_k}{c_k \left... ...\\ [1ex] 0 & \text{for } k \in I_n \backslash I_N . \\ \end{array} \right.$ (2.10)

Then the values 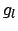$ g_l$ can be obtained from (2.9) by

$\displaystyle g_l = \frac{1}{n}\sum\limits_{k \in I_N} \hat g_k \, {\rm e}^{-2\pi{\mbox{\scriptsize {i}}} \frac{k l}{n}} \qquad (l \in I_n),$    

a FFT of size 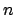$ n$.

This approximation causes an aliasing error.


Stefan Kunis 2004-09-03