Study in Chemnitz. To know what is good.






  • FacebookTwitterYoutube
Polar FFT

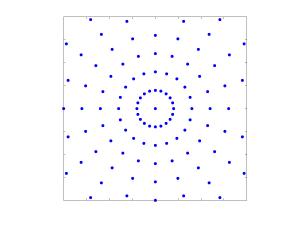
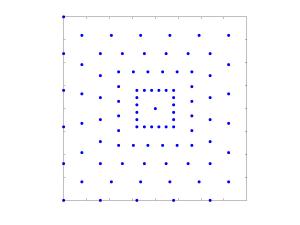
Polar FFT

The polar as well as the pseudo-polar FFT can be computed very accurately and efficiently by the nonequispaced FFT. Furthermore, we apply the reconstruction of a 2d signal from its Fourier transform samples on a (pseudo-)polar grid by means of the inverse nonequispaced FFT.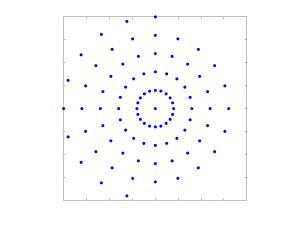

Left to right: polar, modified polar, and linogram grid

We demonstrated that one can compute polar/pseudo-polar FFTs and their inverses very efficiently and accurately.


The algorithms are implemented by Markus Fenn and Stefan Kunis in ./applications/polarFFT. Related paper are

oFenn, M., Kunis, S., and Potts, D.
On the computation of the polar FFT.
Appl. Comput. Harm. Anal. 22, 257-263,   (full paper ps, pdf),   2007

oBöttcher, A. and Potts, D.
Probability against condition number and sampling of multivariate trigonometric random polynomials.
Electron. Trans. Numer. Anal. , 26, 178-189,   (full paper ps, pdf),   2007

oBöttcher, A., Potts, D. and Wenzel, D
A probability argument in favor of ignoring small singular values.
Operator Theory: Advances and Applications, 1, 31-43,   (full paper ps, pdf),   2007