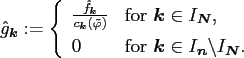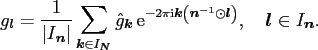Next: The algorithm
Up: NFFT - nonequispaced fast
Previous: The second approximation -
Contents
Starting with the original problem of evaluating the multivariate
trigonometric polynomial in (2.1) one has to do a few
generalisations.
The window function is given by
where 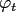 is an univariate window function.
Thus, a simple consequence is
is an univariate window function.
Thus, a simple consequence is
The ansatz is generalised to
where the FFT size is given by
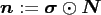 and the
oversampling factors by
and the
oversampling factors by
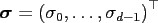 .
Along the lines of (2.7) one defines
.
Along the lines of (2.7) one defines
The values
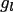 can be obtained by a (multivariate) FFT of size
can be obtained by a (multivariate) FFT of size
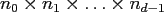 as
as
Using the compactly supported function
![$ \psi\left(\ensuremath{\boldsymbol{x}}\right)=\varphi\left(\ensuremath{\boldsym...
...ght)\chi_{[-{m \over n},{m \over
n}]^d}\left(\ensuremath{\boldsymbol{x}}\right)$](img123.png) ,
one obtains
,
one obtains
where
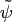 again denotes the one periodic version of
again denotes the one periodic version of 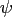 and the
multi-index set is given by
and the
multi-index set is given by




Next: The algorithm
Up: NFFT - nonequispaced fast
Previous: The second approximation -
Contents
Jens Keiner
2006-11-20