



Next: The case
Up: NFFT - nonequispaced fast
Previous: The first approximation -
Contents
If 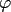 is well localised in time/space domain
is well localised in time/space domain
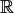 it can be
approximated by a function
it can be
approximated by a function
with
![$ {\rm supp} \, \psi \, \left[-{m \over n},{m \over n}\right], \;m \ll
n,\; m\in \ensuremath{\mathbb{N}}$](img104.png) .
Again, one defines its one periodic version
.
Again, one defines its one periodic version
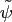 with compact support
in
with compact support
in
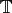 as
as
With the help of the index set
an approximation to 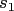 is defined by
is defined by
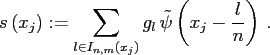 |
(2.8) |
Note, that for fixed
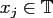 , the above sum contains at most
, the above sum contains at most
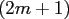 nonzero summands.
nonzero summands.
This approximation causes a truncation error.
Jens Keiner
2006-11-20