M. Pester - LV im SS 2017
  • Anmelden

Übungen zur Arithmetik (2)

( als PDF-Datei )

  1. Bestimmung der Zahl 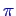\bgroup\color{blue}$\pi$\egroup (=halbe Bogenlänge des Einheitskreises) als obere Grenze der Umfangswerte einbeschriebener regelmäßiger n-Ecke. Für n=2k (k > 1) kann man die Seitenlänge der n-Ecke über die Rekursion
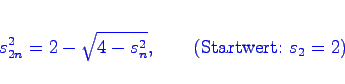
    \begin{displaymath}\bgroup\color{blue} s_{2n}^2 = 2 - \sqrt{4-s_n^2}, \qquad (\mbox{Startwert: }s_2=2) \egroup\end{displaymath}

    bestimmen. Stellen Sie mit Hilfe eines Fortran-Programms fest, wie genau man (bei einfach und doppelt genauer Rechnung) nach dieser Formel die Näherung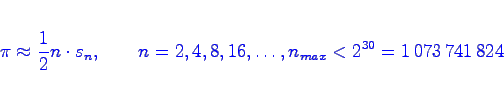
    \begin{displaymath}\bgroup\color{blue} \pi \approx \frac12 n\cdot s_n,\qquad n=2,4,8,16,\ldots,n_{max} < 2^{30}=1\,073\,741\,824 \egroup\end{displaymath}

    erhalten kann (Ausgabe aller Näherungswerte für n=2k,  k=1,2,3,...).

    Suchen Sie nach Ursachen für eventuelle Ungenauigkeiten.
    Formen Sie die Rekursionsformel anschließend äquivalent um, so dass die Berechnung genauer wird.
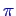    (\bgroup\color{blue}$\pi$\egroup = 3.1415926535897932384626433832795028841971693993751...)

  2. Testen Sie eine weitere Möglichkeit, die Zahl 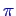\bgroup\color{blue}$\pi$\egroup mittels einer Reihe
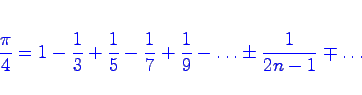
    \begin{displaymath}\bgroup\color{blue} \frac{\pi}4 = 1 - \frac13 +\frac15 -\frac17 +\frac19 -\ldots \pm \frac1{2n-1}\mp \ldots \egroup\end{displaymath}

    zu berechnen, indem Sie jeweils bis zu einer gewünschten Genauigkeit rechnen ( 2 bis 7 gültige Ziffern). Wie steigt die Rechenzeit mit der Genauigkeit?

  3. Bestimmen Sie die Grenzwerte folgender Reihen durch Berechnung der Partialsummen
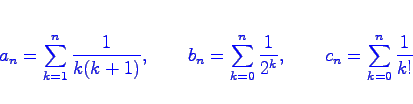
    \begin{displaymath}\bgroup\color{blue} a_n = \sum_{k=1}^n \frac{1}{k(k+1)},\qq... ...^n \frac1{2^k}, \qquad c_n = \sum_{k=0}^n \frac1{k!} \egroup\end{displaymath}

    für n=1,...,nmax, wobei nmax vorher vom Nutzer abgefragt wird.
    Hinweis:
    formatierte Ausgabe aller drei Partialsummen in einer Tabelle 
          write(*,100) n, a, b, c
100   FORMAT( I6,3F20.16 )