|
Aktive Atomnetzwerke in Quasikristallen |
|
Eine selbstkonsistente Rechnung an der Elementazelle des Approximanten
(128 bzw 138 Atome) liefert die Streuphasen der Atome. In einem Superblock aus Elementarzellen (etwa 10000 Atome) werden alle Atome außer das jeweilige Übergangsmetall gestrichem, nur etwa 1000 Atome bleiben. Mit Hilfe einer zweiseitigen Rekursionsmethode (RM) im Rahmen des MTSW-Konzepts wird für ein Atom im Zentrum der Teil der lokalen Zustandsdichte ermittelt, der in einer Rechnung am vollständigen Superblock durch Streuwege entstehen würde, die ausschließlich Übergangsatome enbeziehen. Im Fall des AlCuFe-(1/1)-Approximanten (Cockayne Modell) gleicht das Ergebnis bis auf eine Verschiebung enlang der Energieachse (im Bild nicht gezeigt) dem Ergebnis der ASA-LMTO Rechnung. |
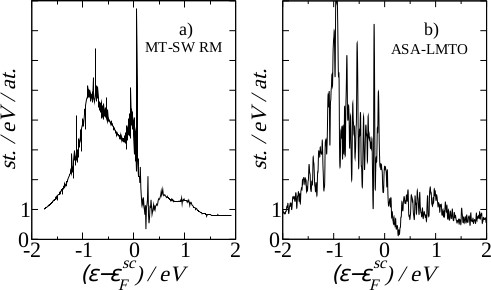 |
| Das Fe-Netzwerk besteht je Zelle aus 12 Fe innerhalb von Bergman clustern und weiteren 4 Fe im glue. Nur bei Einbeziehung der glue-Fe kann sich die atomare d-Resonanz zu einer Netzresonanz entwickeln. Ohne die glue-Fe tritt das tiefe pseudogap nicht auf. |
|
|
Arbeiten zum Thema |
| H. Solbrig, C. V. Landauro,
"Systems with icosahedral clusters: Direct links between atoms in cluster-recursion methods and DOS spectral fine structure", Pbysica B 292(2000)47
|
| H. Solbrig, M. Schubert,
"Towards the influence of the d-resonance splitting on the electronic density of states of an amorphous trnsition metal", J. Phys.: Condens. Matter 4(1992)4441-4457
|
| H. Solbrig,
"Recursive Scattered-Wave Approach to the Electronic Density of States of Topologically Disordered Systems", phys. stat. sol. (b) 139,223(1987)
|
| T. Schmidt, "Saturated bonds and anomalous electronic transport in transition-metal aluminides", Dissertation, Fak. Naturwiss., TU Chemnitz 2006 (diss) |




