


Next: Bibliography
Up: Examples
Previous: CPU-time &
Reconstruction of functions
The usage of the inverse NFFT is e.g. shown in ./example/interpolation_1d, Figure 6, and
./example/glacier, Figure 7. For theoretical result see [16].
Figure:
Real part of different interpolation polynomials for 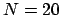 for the
function
for the
function
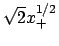 sampled at
sampled at 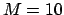 nodes;
nodes; 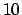 iterations and the six
kernels: Dirichlet, Fejer, Jackson (
iterations and the six
kernels: Dirichlet, Fejer, Jackson (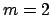 ), Jackson (
), Jackson (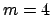 ), Sobolev (
), Sobolev (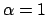 ),
and inverse multi-quadric-type (
),
and inverse multi-quadric-type (
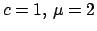 ).
).
|
|
Figure:
Reconstruction of the glacier data set vol87.dat from
[11] with radial (
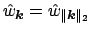 )
inverse multi-quadric-type damping factors (
)
inverse multi-quadric-type damping factors (
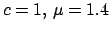 );
);
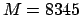 nodes,
nodes, 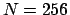 ,
, 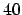 iterations.
iterations.
|
|
Stefan Kunis
2004-09-03