


Next: Reconstruction of functions
Up: Examples
Previous: Accuracy &
Figure 4 compares computational times for both the NDFT and the NFFT, see ./example/timing.
Figure:
The elapsed CPU-time with respect to 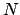 for Kaiser Bessel window, parameters
for Kaiser Bessel window, parameters
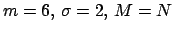 ;
left,
;
left, 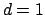 : NDFT (circle), NFFT (no precomputation, x), NFFT (simple interface,
: NDFT (circle), NFFT (no precomputation, x), NFFT (simple interface, 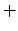 ), NFFT (maximum precomputation, triangle);
middle,
), NFFT (maximum precomputation, triangle);
middle, 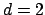 : NDFT (circle), NFFT (simple interface,
: NDFT (circle), NFFT (simple interface, 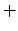 );
right,
);
right, 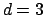 : NDFT (circle), NFFT (simple interface,
: NDFT (circle), NFFT (simple interface, 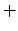 ).
).
|
|
Figure 5 compares computational times for single steps of the NFFT, see ./example/timing.
Figure:
The elapsed CPU-time with respect to 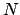 for Kaiser Bessel window, parameters
for Kaiser Bessel window, parameters
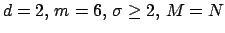 ;
from left to right: multiplication with
;
from left to right: multiplication with
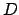 ,
,
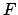 , and
, and
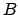 respectively; no precomputation (x),
simple interface (
respectively; no precomputation (x),
simple interface (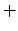 ), and maximum precomputation (triangle).
), and maximum precomputation (triangle).
|
|
Stefan Kunis
2004-09-03