Divalent elements like zinc are close to
![]() where a strong trend towards constructive electronic interference
can be supposed.
We employ the linear muffin-tin orbital method in the atomic-sphere
approximation (LMTO [10]) and calculate the ASDOS
of zinc in the crystalline hcp structure and in the liquid state at 723 K.
The following details of our approach are to be noted:
local exchange-correlation potential [12],
hcp zinc represented by the cubical cell with four atoms,
4096
where a strong trend towards constructive electronic interference
can be supposed.
We employ the linear muffin-tin orbital method in the atomic-sphere
approximation (LMTO [10]) and calculate the ASDOS
of zinc in the crystalline hcp structure and in the liquid state at 723 K.
The following details of our approach are to be noted:
local exchange-correlation potential [12],
hcp zinc represented by the cubical cell with four atoms,
4096 ![]() -points with gaussian broadening of the eigenvalues
(
-points with gaussian broadening of the eigenvalues
(![]() au), liquid zinc represented by a 92-atom supercell
obtained from the experimental
au), liquid zinc represented by a 92-atom supercell
obtained from the experimental ![]() function [11] by means of
a reverse Monte-Carlo method, 20 special
function [11] by means of
a reverse Monte-Carlo method, 20 special ![]() -points are considered
with the same broadening of eigenvalues.
Corresponding LMTO results have been reported by Jank and Hafner [9]
in a more extended study of divalent elements.
They employed 64-atom supercell models of the liquid phases.
-points are considered
with the same broadening of eigenvalues.
Corresponding LMTO results have been reported by Jank and Hafner [9]
in a more extended study of divalent elements.
They employed 64-atom supercell models of the liquid phases.
Fig.2
shows the ASDOS of hcp zinc.
A pronounced pseudogap at the Fermi energy indicates the
stabilizing influence of the electrons.
We obtain the Fermi energy ![]() eV above the bottom of the total
conduction band.
However, this is not the right reference energy
for a reasonable nearly-free electron description at the Fermi level.
Hybridization with the narrow d-band has consequences which
are hardly to estimate.
We proceed as follows:
Non-overlapping muffin-tin spheres (
eV above the bottom of the total
conduction band.
However, this is not the right reference energy
for a reasonable nearly-free electron description at the Fermi level.
Hybridization with the narrow d-band has consequences which
are hardly to estimate.
We proceed as follows:
Non-overlapping muffin-tin spheres (![]() au) are put into
the atomic spheres (
au) are put into
the atomic spheres (![]() au).
The average potential between the two spheres (muffin-tin zero)
is our choice of the reference energy.
This provides
au).
The average potential between the two spheres (muffin-tin zero)
is our choice of the reference energy.
This provides ![]() eV=0.614 au,
eV=0.614 au,
![]()
![]() ,
,
![]() au, the scattering phase shifts
au, the scattering phase shifts
![]() ,
,
![]() =0.2340,
=0.2340,
![]() and the bare ASDOS
and the bare ASDOS
![]() states/eV,
states/eV,
![]() states/eV
and
states/eV
and
![]() states/eV.
Contributions with
states/eV.
Contributions with ![]() are disregarded in the following.
are disregarded in the following.
We will demonstrate that the stable shell sequence even of hcp zinc
meets the requirements of stability as derived in the former section
from the interference of scattering-path loops with only one scattering event.
Fig.3
shows the pair correlation function ![]() of hcp zinc,
where an additional radial gaussian broadening is applied (
of hcp zinc,
where an additional radial gaussian broadening is applied (![]() au).
au).
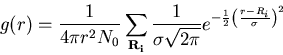 |
(19) |
The results with liquid zinc are less conclusive (
(Fig.2).
A possible weak pseudogap is seen below ![]() .
This challenges some comment.
As a first peculiarity, the pseudogap at
.
This challenges some comment.
As a first peculiarity, the pseudogap at ![]() may be blurred by
residual oscillations due to the incomplete
may be blurred by
residual oscillations due to the incomplete ![]() -space treatment.
However, this should not account for the obvious shift to lower energy.
Note as a second peculiarity that really an artificial neighbour-shell
sequence enters the LMTO calculation upon applying periodic boundary
conditions, in particular if small supercells with only 64 or 92 atoms
are used.
Suppose the discussion of the former section applies,
i.e. the pseudogap at
-space treatment.
However, this should not account for the obvious shift to lower energy.
Note as a second peculiarity that really an artificial neighbour-shell
sequence enters the LMTO calculation upon applying periodic boundary
conditions, in particular if small supercells with only 64 or 92 atoms
are used.
Suppose the discussion of the former section applies,
i.e. the pseudogap at ![]() is controlled by the interference
of scattered waves which emerge from the stack of neighbour shells.
In liquid metals, there are only four or five shells.
They occupy distances where dominating short-range effects must
be expected due to higher angular momenta.
On such conditions, a weak pseudogap at
is controlled by the interference
of scattered waves which emerge from the stack of neighbour shells.
In liquid metals, there are only four or five shells.
They occupy distances where dominating short-range effects must
be expected due to higher angular momenta.
On such conditions, a weak pseudogap at ![]() should very sensitively
depend on the medium-range order which really acts in the supercell
calculation.
Fig.4
shows the effective pair correlation function which enters our
LMTO calculation.
It is derived from the content of our 92-atom supercell upon applying
periodic boundary conditions with a gaussian broadening (
should very sensitively
depend on the medium-range order which really acts in the supercell
calculation.
Fig.4
shows the effective pair correlation function which enters our
LMTO calculation.
It is derived from the content of our 92-atom supercell upon applying
periodic boundary conditions with a gaussian broadening (![]() au).
The shells beyond the basic cube are slightly too wide.
Moreover, due to the periodic translation of the supercell
and in contrast to the experiment [11] the artificial
shell structure continues up to large distances.
Hence, with the excessive shell spacing the pseudogap must occur at
lower energies.
The absence of pseudogaps precisely at
au).
The shells beyond the basic cube are slightly too wide.
Moreover, due to the periodic translation of the supercell
and in contrast to the experiment [11] the artificial
shell structure continues up to large distances.
Hence, with the excessive shell spacing the pseudogap must occur at
lower energies.
The absence of pseudogaps precisely at ![]() in the results of small-supercell
calculations for liquid zinc cannot be taken as a proof.
Larger supercells are required which comprise themselves the proper
shell sequence.
Moreover, unphysical long-range tails due to the employed periodic
boundary conditions are to be suppressed.
in the results of small-supercell
calculations for liquid zinc cannot be taken as a proof.
Larger supercells are required which comprise themselves the proper
shell sequence.
Moreover, unphysical long-range tails due to the employed periodic
boundary conditions are to be suppressed.