In this section both the ![]() and the
and the ![]() scattering in the environment
are considered to act on both the
scattering in the environment
are considered to act on both the ![]() and the
and the ![]() ASDOS.
Again, we start from the single-scattering approximation (12)
to the
ASDOS.
Again, we start from the single-scattering approximation (12)
to the
![]() and obtain
and obtain
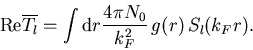 |
(16) |
| (17) | |||
| (18) | |||
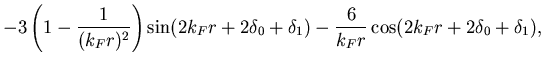 |
|||
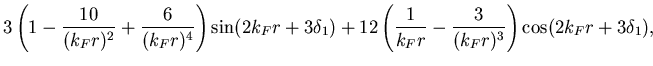 |
|||
 |
The following general conclusions can be drawn:
(i) According to (10,16) low
![]() is obtained if the shells (the maxima of
is obtained if the shells (the maxima of ![]() ) coincide with
the minima of
) coincide with
the minima of ![]() .
However, stability requires low total ASDOS,
.
However, stability requires low total ASDOS,
![]() .
The really stable shell sequence will thus result from the competition
between
.
The really stable shell sequence will thus result from the competition
between
![]() and
and
![]() .
(ii) Asymptotically, the shells must be uniformly spaced with the
Friedel wave length,
.
(ii) Asymptotically, the shells must be uniformly spaced with the
Friedel wave length,
![]() .
This is just the demand of the Nagel-Tauc condition.
The distant shells act "in phase" on the central atomic sphere.
(iii) At smaller distances, the polynomials of powers of
.
This is just the demand of the Nagel-Tauc condition.
The distant shells act "in phase" on the central atomic sphere.
(iii) At smaller distances, the polynomials of powers of
![]() (18) give rise to deviations from the extrapolated
asymptotic bahaviour.
This is due to the
(18) give rise to deviations from the extrapolated
asymptotic bahaviour.
This is due to the ![]() scattering in the environment.
Note that the cosine terms decay only as
scattering in the environment.
Note that the cosine terms decay only as ![]() and act thus
up to considerable distances.
The short-range sensitivity is increased due to the higher powers of
and act thus
up to considerable distances.
The short-range sensitivity is increased due to the higher powers of
![]() .
On the other hand, contraction and dilation of the close neighbour shells
may also arise from the involved higher electronic angular momenta.
(iv) The condition
.
On the other hand, contraction and dilation of the close neighbour shells
may also arise from the involved higher electronic angular momenta.
(iv) The condition
![]() defines the remarkable situation
where the standards (18) have no long-range parts.
The asymptotic contributions due to
defines the remarkable situation
where the standards (18) have no long-range parts.
The asymptotic contributions due to ![]() and
and ![]() scattering in the environment
cancel out each other.
On such conditions, the system gets short-range confined.
It must be stressed again that the above conclusions are drawn from
single-scattering formulas.
They are derived from the state of the electronic interference which
in turn is a guide line for the multiple scattering.
scattering in the environment
cancel out each other.
On such conditions, the system gets short-range confined.
It must be stressed again that the above conclusions are drawn from
single-scattering formulas.
They are derived from the state of the electronic interference which
in turn is a guide line for the multiple scattering.