We deal with the local electronic density of states of atomic spheres
(ASDOS) within the multiple-scattering approach.
A model is adopted where the same representative
muffin-tin (MT) potential is put into each atomic sphere.
![]() ,
, ![]() ,
, ![]() and
and
![]() designate the
electron energy, the angular momentum, the MT scattering phase shifts
and the partial scattering amplitudes, respectively.
The partial ASDOS of the embedded atomic sphere number
designate the
electron energy, the angular momentum, the MT scattering phase shifts
and the partial scattering amplitudes, respectively.
The partial ASDOS of the embedded atomic sphere number ![]() ,
,
| (10) |
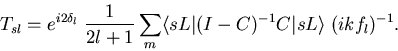 |
(11) |
We want to know the radial sequence of neighbour shells which provides
low ASDOS at the Fermi energy.
Suppose an approximation to the ensemble average of the
environment correction (11)
where the pair correlation function ![]() is compared with
certain standards of the radial behaviour similar to the
is compared with
certain standards of the radial behaviour similar to the
![]() in (7).
In that case the neighbour-shell radii and the radii where the
standards have extreme values have to be correlated in just the same
way as demonstrated in connection with (7) and (8).
This kind of approximation to (11) is obtained upon confining
to single-scattering in the environment (
in (7).
In that case the neighbour-shell radii and the radii where the
standards have extreme values have to be correlated in just the same
way as demonstrated in connection with (7) and (8).
This kind of approximation to (11) is obtained upon confining
to single-scattering in the environment (![]() replaced
by
replaced
by ![]() ).
The ensemble average can be performed and we arrive at
).
The ensemble average can be performed and we arrive at
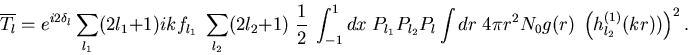 |
(12) |
The following items are to be noted:
(i) Similar to (7) one finds in (12) the pair correlation function ![]() correlated with certain standards of the radial behaviour,
correlated with certain standards of the radial behaviour,
![]() .
At
.
At ![]() the atomic spheres resolve the close-range behaviour
of the neighbour-shell sequence
the atomic spheres resolve the close-range behaviour
of the neighbour-shell sequence ![]() via Fresnel-type diffraction.
This is beyond the information extracted by
via Fresnel-type diffraction.
This is beyond the information extracted by ![]() in (7).
(ii) Hybridization effects are represented by
scattering-path loops which include at least three scattering events
with two different angular-momentum channels of the considered atomic sphere.
Hybridization is thus disregarded in (12).
Nevertheless, the hybridizing elements of the linking matrix
in (7).
(ii) Hybridization effects are represented by
scattering-path loops which include at least three scattering events
with two different angular-momentum channels of the considered atomic sphere.
Hybridization is thus disregarded in (12).
Nevertheless, the hybridizing elements of the linking matrix ![]() which
are non-diagonal in the angular momentum contribute in (12).
which
are non-diagonal in the angular momentum contribute in (12).
The Nagel-Tauc stability concept demands a minimum
of the ASDOS at the Fermi energy.
According to (10) ASDOS minima arise from strongly negative values
of Re
![]() .
In the following, employing the single-scattering approximation (12),
the trends are inferred which follows the neighbour-shell sequence
in order to achieve low ASDOS at
.
In the following, employing the single-scattering approximation (12),
the trends are inferred which follows the neighbour-shell sequence
in order to achieve low ASDOS at ![]() .
.