The Fermi sphere, the interference cube and
![]() are connected by the well-known free-electron relation
are connected by the well-known free-electron relation
| (1) |
In order to answer this question we associate
the six quadratic surface planes of the interference cube
with corresponding parts of the Fermi surface:
As seen from the common center of the two bodies,
each quadratic face fills a solid angle of 4![]() /6=2
/6=2![]() /3.
We conclude that each quadratic face is "responsible" for just
the part of the Fermi surface which belongs to its solid angle (fig.1b).
Suppose a cap (solid angle
/3.
We conclude that each quadratic face is "responsible" for just
the part of the Fermi surface which belongs to its solid angle (fig.1b).
Suppose a cap (solid angle ![]() ) of each
) of each ![]() /3 Fermi surface
lies outside the interference cube and
the rest, 2
/3 Fermi surface
lies outside the interference cube and
the rest, 2![]() /3 -
/3 - ![]() , lies inside.
The following statement is fundamental for this approach:
Transitions which start at any point of any cap outside the interference cube
and terminate on the opposit side at any point inside the interference cube
have one component of the momentum transfer
approximately equal to the side length of the interference cube.
Hence, they are accompanied by constructive interference.
Just the same holds for the inside-outside transitions.
, lies inside.
The following statement is fundamental for this approach:
Transitions which start at any point of any cap outside the interference cube
and terminate on the opposit side at any point inside the interference cube
have one component of the momentum transfer
approximately equal to the side length of the interference cube.
Hence, they are accompanied by constructive interference.
Just the same holds for the inside-outside transitions.
Now, the condition for most-constructive interference among scattered waves
can be set up:
The total number of transitions, ![]() ,
is proportional to
,
is proportional to ![]() .
The part
.
The part ![]() of them which is accompanied by almost
constructive interference will be proportional to
of them which is accompanied by almost
constructive interference will be proportional to
| (2) |
 |
(3) |
| (4) |
The present treatment proceeds as follows:
(i) A model is postulated which describes the behaviour of the electrons at
the Fermi surface.
(ii) Employing this model, the conditions (3) and (4) are obtained
which ensure that the electrons respond most efficiently to the ions.
Former estimates of the critical electron concentration
have accounted for the perturbing influence of the core electrons.
The results scatter from 1.7 [3] to values between
1.7 and 2.5 [6].
Haeussler [4] estimated values below 2.0 in order to
achieve a space-filling arrangement of Fermi spheres.
Our final relation (3) can be contrasted with empirical results
for certain metallic alloys where the diffraction behaviour
is reasonably approximated by packings of almost equally-sized spheres.
Blétry [7] reported for such alloys
that both the packing fraction, ![]() ,
and the position of the first diffraction peak,
,
and the position of the first diffraction peak, ![]() ,
are well represented by
,
are well represented by
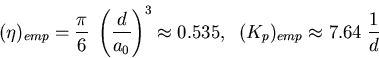 |
(5) |
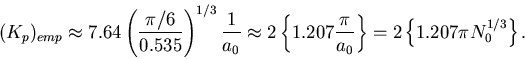 |
(6) |