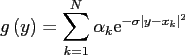Next: Summation of zonal functions
Up: Applications
Previous: Summation of smooth and
Contents
This is a special case of the fast summation method, we compute approximations
of the following sums.
Given complex coefficients
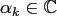 and source nodes
and source nodes
![$ x_k\in[-\frac{1}{4},\frac{1}{4}]$](img497.png) , our goal consists in the fast evaluation
of the sum
, our goal consists in the fast evaluation
of the sum
at the target nodes
![$ y_j \in [-\frac{1}{4},\frac{1}{4}]$](img499.png) ,
,
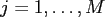 ,
where
,
where
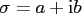 ,
, 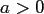 ,
,
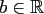 , denotes a complex parameter.
For details see [37] and the related paper [2] for
applications.
All numerical examples of [37] are produced by the programs in applications/fastgauss.
, denotes a complex parameter.
For details see [37] and the related paper [2] for
applications.
All numerical examples of [37] are produced by the programs in applications/fastgauss.
Jens Keiner
2006-11-20
![]() and source nodes
and source nodes
![]() , our goal consists in the fast evaluation
of the sum
, our goal consists in the fast evaluation
of the sum