Next: Fast Gauss transform
Up: Applications
Previous: Applications
Contents
We are interested in the fast evaluation of linear combinations of radial
functions, i.e. the computation of
for
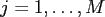 and nodes
and nodes
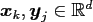 .
For smooth kernels
.
For smooth kernels 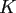 with an additional parameter
with an additional parameter 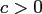 , e.g. the Gaussian
, e.g. the Gaussian
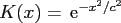 , the multiquadric
, the multiquadric
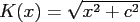 or the inverse
multiquadric
or the inverse
multiquadric
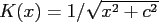 our algorithm requires
our algorithm requires
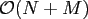 arithmetic operations.
In the case of singular kernels
arithmetic operations.
In the case of singular kernels 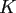 , e.g.,
, e.g.,
an additional regularisation procedure must be incorporated and the algorithm
has the arithmetic complexity
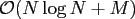 or
or
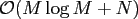 if
either the target nodes
if
either the target nodes
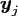 or the source nodes
or the source nodes
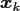 are
``reasonably uniformly distributed''.
are
``reasonably uniformly distributed''.
Note that the proposed fast algorithm [49,50,23]
generalises the diagonalisation of convolution matrices by Fourier matrices to
the setting of arbitrary nodes.
In particular, this yields nearly the same arithmetic complexity as the FMM
[5] while allowing for an easy change of various kernels.
A recent application in particle simulation is given in [43].
The directory applications/fastsum contains C and MATLAB programs
that show how to use the fast summation method.




Next: Fast Gauss transform
Up: Applications
Previous: Applications
Contents
Jens Keiner
2006-11-20