



Next: Fast Gaussian gridding
Up: Available window functions and
Previous: Tensor product based precomputation
Contents
For a large number of nodes 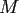 , the amount of memory can by further reduced
by the use of lookup table techniques.
For a recent example within the framework of gridding see [6].
We suggest to precompute from the even window function the equidistant samples
, the amount of memory can by further reduced
by the use of lookup table techniques.
For a recent example within the framework of gridding see [6].
We suggest to precompute from the even window function the equidistant samples
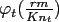 for
for
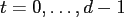 and
and
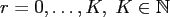 and then compute for the actual node
and then compute for the actual node
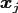 during the NFFT the values
during the NFFT the values
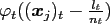 for
for
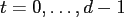 and
and
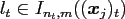 by means of the linear interpolation from its two
neighbouring precomputed samples.
by means of the linear interpolation from its two
neighbouring precomputed samples.
This method needs only a storage of 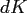 real numbers in total where
real numbers in total where 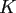 depends solely on the target accuracy but neither on the number of nodes
depends solely on the target accuracy but neither on the number of nodes 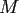 nor on the multidegree
nor on the multidegree
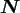 .
Choosing
.
Choosing 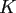 to be a multiple of
to be a multiple of 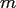 , we further reduce the computational
costs during the interpolation since the distance from
, we further reduce the computational
costs during the interpolation since the distance from
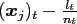 to the two neighbouring interpolation nodes and hence the
interpolation weights remain the same for all
to the two neighbouring interpolation nodes and hence the
interpolation weights remain the same for all
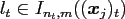 .
This method requires
.
This method requires 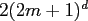 extra multiplications per node and is
used within the NFFT by the flag PRE_LIN_PSI. Error estimates for this approximation are given in [36].
extra multiplications per node and is
used within the NFFT by the flag PRE_LIN_PSI. Error estimates for this approximation are given in [36].




Next: Fast Gaussian gridding
Up: Available window functions and
Previous: Tensor product based precomputation
Contents
Jens Keiner
2006-11-20
![]() real numbers in total where
real numbers in total where ![]() depends solely on the target accuracy but neither on the number of nodes
depends solely on the target accuracy but neither on the number of nodes ![]() nor on the multidegree
nor on the multidegree
![]() .
Choosing
.
Choosing ![]() to be a multiple of
to be a multiple of ![]() , we further reduce the computational
costs during the interpolation since the distance from
, we further reduce the computational
costs during the interpolation since the distance from
![]() to the two neighbouring interpolation nodes and hence the
interpolation weights remain the same for all
to the two neighbouring interpolation nodes and hence the
interpolation weights remain the same for all
![]() .
This method requires
.
This method requires ![]() extra multiplications per node and is
used within the NFFT by the flag PRE_LIN_PSI. Error estimates for this approximation are given in [36].
extra multiplications per node and is
used within the NFFT by the flag PRE_LIN_PSI. Error estimates for this approximation are given in [36].