



Next: Linear interpolation from a
Up: Available window functions and
Previous: Fully precomputed window function
Contents
Using the fact that the window functions are built as tensor products one can
store
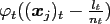 for
for
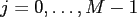 ,
,
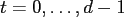 , and
, and
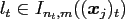 where
where
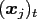 denotes the
denotes the 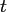 -th component of the
-th component of the 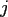 -th node.
This method uses a medium amount of memory to store
-th node.
This method uses a medium amount of memory to store 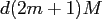 real numbers
in total.
However, one has to carry out for each node at most
real numbers
in total.
However, one has to carry out for each node at most 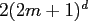 extra
multiplications to compute from the factors the multivariate window function
extra
multiplications to compute from the factors the multivariate window function
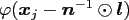 for
for
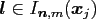 .
Note, that this technique is available for every window function discussed
here and can be used by means of the flag PRE_PSI which is also the
default method within our software library.
.
Note, that this technique is available for every window function discussed
here and can be used by means of the flag PRE_PSI which is also the
default method within our software library.
Jens Keiner
2006-11-20