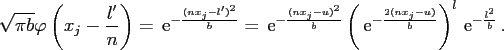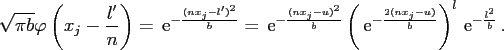Next: No precomputation of the
Up: Available window functions and
Previous: Linear interpolation from a
Contents
Two useful properties of the Gaussian window function (2.9) within
the present framework were recently reviewed in [29].
Beside its tensor product structure for 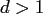 , which also holds for all other
window functions, it is remarkable that the number of evaluations of the form
exp() can be greatly decreased.
More precisely, for
, which also holds for all other
window functions, it is remarkable that the number of evaluations of the form
exp() can be greatly decreased.
More precisely, for 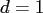 and a fixed node
and a fixed node 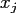 the evaluations of
the evaluations of
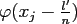 ,
,
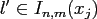 , can be reduced by the
splitting
, can be reduced by the
splitting
where
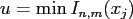 and
and
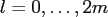 .
Note, that the first factor and the exponential within the brackets are
constant for each fixed node
.
Note, that the first factor and the exponential within the brackets are
constant for each fixed node 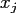 .
Once, we evaluate the second exponential, its
.
Once, we evaluate the second exponential, its 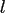 -th power can be computed
consecutively by multiplications only.
Furthermore, the last exponential is independent of
-th power can be computed
consecutively by multiplications only.
Furthermore, the last exponential is independent of 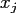 and these
and these 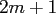 values are computed only once within the NFFT and their amount is negligible.
Thus, it is sufficient to store or evaluate
values are computed only once within the NFFT and their amount is negligible.
Thus, it is sufficient to store or evaluate 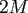 exponentials for
exponentials for 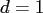 .
The case
.
The case 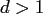 uses
uses 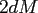 storages or evaluations by using the general tensor
product structure.
This method is employed by the flags FG_PSI and PRE_FG_PSI for
the evaluation or storage of
storages or evaluations by using the general tensor
product structure.
This method is employed by the flags FG_PSI and PRE_FG_PSI for
the evaluation or storage of 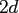 exponentials per node, respectively.
exponentials per node, respectively.




Next: No precomputation of the
Up: Available window functions and
Previous: Linear interpolation from a
Contents
Jens Keiner
2006-11-20