Johannes Kepler, 1571–1630.
Monument in Linz

Hommage à Johannes Kepler

See the derivation from Newton's laws >>here.

In 1609, J. Kepler publishes his first two laws in astronomia nova. They can be employed to locate bodies as planets, the moon, comets, the International Space Station (ISS), satellites etc. Here we describe all ingredients to compute the exact position of orbiting objects based on the 6 Keplerian elements, and apply them to find the planets on the sky. It will become apparent that Kepler's contributions constitute amazing achievements in science.

Kepler orbits

The position of the orbiting body along its orbit

Following Kepler's 1^st law, the orbits are ellipses. Let $a$ denote the semi-major axis and $e$ the eccentricity of the ellipse. Then the planar coordinates of the object in its orbital plane are $$x_t= a(\cos(E)- e),\quad y_t=a\sqrt{1-e^2}\sin(E),$$ where the parametric angle $E$ is called eccentric anomaly. This ellipse is shifted by -a e so that its right focus (the Sun) is in the origin.
The eccentric anomaly E is not linear in time, because the orbiting object is faster if close to the Sun. Denote by $M=M_0+\frac{t-t_0}{U}360°$ the mean anomaly, which evolves linearly in time $t$.

Kepler's famous equation $$M=E- e\cdot\sin E,$$ a consequence of Kepler's second law, relates the eccentric anomaly E and the mean anomaly M. Kepler's equation needs to be solved to position the body. This can be achieved by iterating, e.g., as $e < 1$. A useful approximation for small e is the Taylor series approximation $E=M+ e \sin(M)+ \frac{e^2}{2}\sin(2M)+\mathcal{O}(e^3)$. In 1818, Friedrich Bessel found the fascinating, closed form solution $$E=M+\sum_{n=1}\frac{2}{n}J_n(n e)\sin(n M)$$ of Kepler's nonlinear equation in terms of a Fourier-Kapteyn series ($J_n$ are Bessel functions of the first kind).

Keplerian elements (orbital elements)

Six parameters are enough to locate an orbiting object in the sky and for many objects they are listed in tables.

Google's doodle celebrating Kepler's birthday.
The orbit is an ellipse, and
the body is faster close to the Sun.

The 6 Keplerian elements are:

• The semi-major axis $a$ and
• the eccentricity $e$, describing the size and shape of the orbit.
• The inclination $I$ and
• longitude of the ascending node $\Omega$ describing the orientation of the orbital plane.
• The argument of periapsis (or argument of perihelion) $\omega$ specifies the orientation of the ellipse within its orbital plane,
• the mean anomaly $M$ parametrizes the object's motion along its orbit (with orbital period U) over time.

Kepler orbits for planets

The tables for the time dependent Keplerian elements can be found in many places, the numbers below are adapted from NASA.

Planet	period U/ y	$a$/ au*, **	$e$	$I$	$\Omega$	$\omega$	$M_0$
Mercury ☿	0.241	0.387	20.6%	7.00°	48.3°	29.13°	174.8°
Venus ♀	0.615	0.723	0.67%	3.39°	76.7°	54.92°	50.37°
Earth ♁	1.000	1.000	1.67%	0.00°	0.00°	102.9°	357.5°
Mars ♂	1.881	1.524	9.34%	1.85°	49.6°	284.5°	19.39°
Jupiter ♃	11.86	5.203	4.84%	1.30°	100.5°	274.3°	19.67°
Saturn ♄	29.45	9.537	5.39%	2.49°	113.7°	338.9°	317.4°

^* $U^2=a^3$ by Kepler's 3^rd law.
^** 1 au= 1.5·10⁸ km (astronomical unit) is the distance from the Earth to the Sun,
for which the light needs about 8.3 minutes.

This table comprises the visible planets. The table is valid with an error less than 0.2° in the actual position. Aberrations are caused by the fact that planets interfere among themselves.
The complete (nonrelativistic) dynamics were given by Isaac Newton, who published his Philosophiae Naturalis Principia Mathematica almost 80 years later. Albert Einstein found the relativistic corrections.

Celestial coordinates

Tycho Brahe, 1546–1601,
Johannes Kepler, 1571–1630.
Monument in Prague

Ecliptic and equatorial coordinates

Ecliptic coordinates are with respect to the Earth's orbital plane around the Sun. The Sun is the origin of the heliocentric ecliptic coordinate system.
(Heliocentric) equatorial coordinates are given in the plane of the Earth's equator with Sun in the origin. By further conventions on the axes they are related by $$\begin{pmatrix}x_{eq}\\y_{eq}\\z_{eq} \end{pmatrix}=\begin{pmatrix}1 & 0 & 0\\ 0 & \cos\varepsilon & -\sin\varepsilon\\ 0 & \sin\varepsilon & \cos\varepsilon \end{pmatrix}\begin{pmatrix}x_{ecl}\\y_{ecl}\\z_{ecl} \end{pmatrix},$$ where the Earth's obliquity is $\varepsilon= 23.43928°$.
Equatorial coordinates, expressed in spherical coordinates, are used to locate stars. The transformation is \begin{eqnarray*} x_{eq} & = & r\cos\delta\cos\alpha,\\ y_{eq} & = & r\cos\delta\sin\alpha,\\ z_{eq} & = & r\sin\delta, \end{eqnarray*} where $\alpha$ is called (right) ascension (ascensio recta, lat.) and $\delta$ is declination (declinatio, lat.). The right ascension is typically given in hours, where 24^h= 360° (i.e., 1^h= 15°).
Importantly, the equatorial coordinates of a star are the same for every observer on the Earth. As en example, Vega (the 2^nd brightest star in the northern hemisphere) can be found at $\alpha=$ 18^h37^m, $\delta=$ 38°47'.

Sidereal time

Sidereal time is measured by the rotation of the Earth with respect to the stars (rather than relative to the Sun). One sidereal day corresponds to the time taken for the Earth to rotate once with respect to the stars. The Earth's rotation around the Sun during a solar year accumulates for one additional sidereal day. The sidereal day thus is shorter, it lasts approximately 23 h 56 min 4.0916 s.
Given the coordinated universal time (UTC) $t_{UTC}$, the local sidereal time depending on the observer's longitude $\lambda_0$ is $$LST/ d= \left(1+\frac{1}{365.242189}\right)*(t_{UTC}-t_{\text{1. Jan. 2000, 12h}})/ d+0.7790572733+ \frac{\lambda_0}{360°}$$ with a precision of 0.1 seconds per century. The local sidereal time is adjusted for Greenwich at noon on Jan. 1^st, 2000 and expressed in days (d). Local sidereal time as well corresponds to the right ascension $\alpha$ (equatorial coordinate) of a star on the observer's meridian (for this reason right ascension is measured in hours).

Horizontal coordinates

Horizontal coordinates

The observer on the Earth's surface will see the object with equatorial coordinates $(\alpha,\delta)$ in his own, horizontal coordinates $(A,a)$. A is called azimuth, and a altitude (or elevation). This system is occasionally called az/el-system. The horizontal coordinates depend on

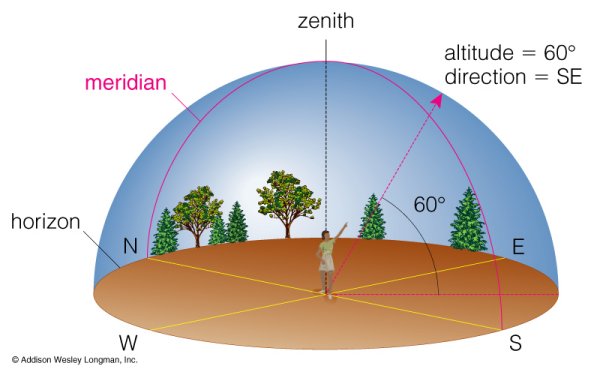
• the ecliptic coordinates $(\alpha,\delta)$,
• the local sidereal time LST and
• the geographical coordinates of the observer at longitude $\lambda_0$ and latitude $\varphi_0$.

The transformation \begin{eqnarray*} \tan(A)& = & \frac{\sin(LST-\alpha)}{\cos(LST-\alpha)\sin(\varphi_0)-\tan(\delta)\cos(\varphi_0)},\\ \sin(a)& = & \sin(\varphi_0)\sin(\delta)+\cos(\varphi_0)\cos(\delta)\cos(LST-\alpha) %\sin(A)& = & -\frac{\sin(LST-\alpha)\cos(\delta)}{\cos(a)}\,\text{or}\\ %\cos(A)& = & \frac{\sin(\delta)-\sin(a)\sin(\varphi)}{\cos(a)\cos(\varphi)}\\ \end{eqnarray*} is found by employing the law of the cosine from spherical trigonometry to the astronomical triangle, a triangle on the sphere. The quantity $h= LST\frac{360°}{24^h}-\alpha$ is also called local hour angle.
Because of the atmosphere's refraction and the solar disc parameter the sun rises and sets already for $a=-0.83°$. It is recommended to use atan2 to compute the azimuth angle.
 

The position of the orbit

Flip the orbiting object with planar coordinates $(x_t,y_t,0)$ to (heliocentric) ecliptic coordinates with respect to the angles $\Omega, I, \omega$ (Keplerian elements, cf. also Euler angles) by rotating backwards, $$\begin{pmatrix}x_{ecl}\\y_{ecl}\\z_{ecl}\end{pmatrix}= \begin{pmatrix} \cos\Omega & -\sin\Omega & 0\\ \sin\Omega & \cos\Omega & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos I & -\sin I\\ 0 & \sin I & \cos I \end{pmatrix} \begin{pmatrix} \cos\omega & -\sin\omega & 0\\ \sin\omega & \cos\omega & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix}x_t\\y_t\\0\end{pmatrix}.$$ $(x_{ecl}, y_{ecl}, z_{ecl})$ is the position of the orbiting object in heliocentric ecliptic coordinates. The Earth's position has to be subtracted to obtain geocentric ecliptic coordinates. Horizontal coordinates (A,a) are finally obtained as outlined above.

Planets and the Sun

Actual positions of the planets can be computed online here: online positioning.

The orbit of the International Space Station, ISS

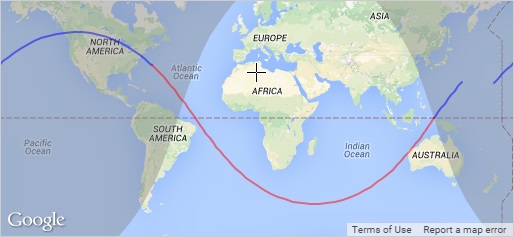The international space station is the brightest spot on the sky, if visible. Check if you can see the ISS today and follow its orbit here, ISS.

The analemma in Bergamo

The Earth reaches its perihelion (its nearest point to the Sun on the orbit) around January 3^rd and its aphelion around July 4^th (the date cannot be given more precisely, as the moon has some influence here). As a consequence of Kepler's 2^nd law, the earth is faster close to the Sun, and consequently the solar noons differ from day to day, during acceleration. The gap is up to 17 minutes and visualized by an analemma. In Bergamo, the anelemma is engraved in stone.

Corrections, improvements and suggestions are welcome at alois.pichler (at) univie.ac.at.
Math rendered by MathJax.