Ellipse

Rectangular coordinates

The equations $\sqrt{(x-e)^2+y^2}+\sqrt{(x+e)^2+y^2}=2a$ and \begin{equation}\label{eq:1} \left(\frac{x}{a}\right)^2+\left(\frac{y}{b}\right)^2=1 \end{equation} are equivalent, they define the same ellipse in rectangular coordinates.

• $e$ is the focal distance or linear eccentricity,
• $a$ is the semi-major axis,
• $b^2:=a^2-e^2$ is the semi-minor axis and
• $\varepsilon:=\frac{e}{a}=\sqrt{1-\frac{b^2}{a^2}}$ is the eccentricity.

Polar coordinates

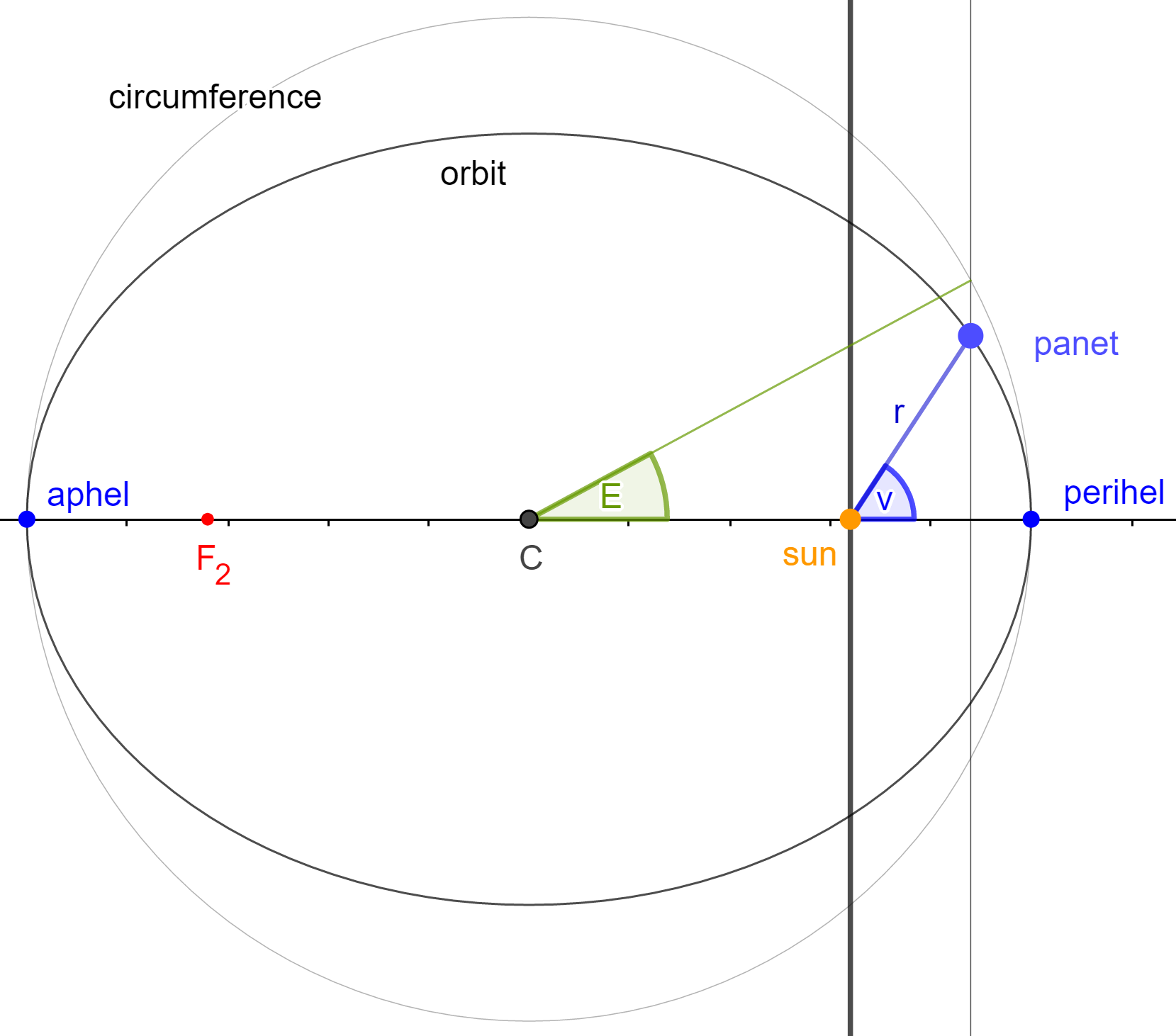
Important angles to describe the ellipse include

• the eccentric anomaly $E$ and
• the true anomaly $\nu$.

Polar form with respect to the center

Employing polar coordinates $(r_c,\varphi_c)$ with respect to the center the points of the ellipsoid are \begin{equation}\label{eq:2} \begin{pmatrix}x\\y\end{pmatrix} =\begin{pmatrix}a \cos E\\b \sin E\end{pmatrix} =r_c\begin{pmatrix}\cos \varphi_c\\\sin \varphi_c\end{pmatrix}. \end{equation} The relation $\tan \varphi_c=\frac{b}{a}\tan E$ derives from \eqref{eq:2} and the polar form \[r_c(\varphi_c)=\frac{b}{\sqrt{1-\varepsilon^2 \cos^2\varphi_c}}\] from \eqref{eq:1}.

Polar form with respect to the focus

The position, expressed in polar coordinates $(r,\nu)$ as seen from the focus $(e,0)$, is \begin{equation}\label{eq:3} \mathbf r= a \begin{pmatrix}\cos E-\varepsilon\\\sqrt{1-\varepsilon^2} \sin E\end{pmatrix} =r \begin{pmatrix}\cos\nu\\\sin\nu\end{pmatrix}. \end{equation} It follows from \eqref{eq:3} that $\tan\nu=\frac{\sqrt{1-\varepsilon^2} \sin E}{\cos E-\varepsilon}$, or equivalently, \[\tan\frac{\nu}{2} =\sqrt{\frac{1+\varepsilon}{1-\varepsilon}}\tan\frac{E}{2} =\frac{\sqrt{1+\varepsilon}\sin\frac{E}{2}}{\sqrt{1-\varepsilon}\cos\frac{E}{2}}. \] The radius $r=a(1-\varepsilon\cos E)$ and the polar form of the ellipse (with respect to the focus) \begin{equation}\label{eq:ell} r(\nu)=a\frac{1-\varepsilon^2}{1+\varepsilon\cos\nu} \end{equation} are immediate from \eqref{eq:3}.

Kepler orbits

From Newton's 2^nd law of motion and Newton's universal law of gravitatioin it follows that \begin{equation}\label{eq:Newton} m \ddot{\mathbf r}= -G \frac{m M}{|\mathbf r|^2}\frac{\mathbf r}{|\mathbf r|}. \end{equation} The angular momentum $\mathbf H:=\mathbf r\times\dot{\mathbf r}$ satisfies \[\frac{d}{dt}(\mathbf r\times\dot{\mathbf r})= \dot{\mathbf r}\times\dot{\mathbf r}+\mathbf r\times\ddot{\mathbf r}=0\] by \eqref{eq:Newton}, so that the motion is in a plane and we can assume that \[\mathbf r(t)= r(t)\begin{pmatrix}\cos\nu(t)\\\sin\nu(t)\end{pmatrix}. \] Note that $H:=|\mathbf r\times\dot{\mathbf r}|=\left|r\begin{pmatrix}\cos\nu\\\sin\nu\end{pmatrix}\times\left(\dot r\begin{pmatrix}\cos\nu\\\sin\nu\end{pmatrix} + r\dot\nu\begin{pmatrix}-\sin\nu\\\cos\nu\end{pmatrix}\right)\right|=r^2\dot\nu$ is constant. It follows from \eqref{eq:Newton} that \[\ddot{\mathbf r}=(\ddot r-r\dot\nu^2)\begin{pmatrix}\cos\nu\\ \sin\nu\end{pmatrix} + (2\dot r\dot\nu+r\ddot\nu)\begin{pmatrix}-\sin\nu\\ \cos\nu\end{pmatrix}=-\frac{GM}{r^2}\begin{pmatrix}\cos\nu\\\sin\nu\end{pmatrix}.\] Now $2\dot r\dot\nu+r\ddot\nu=0$ integrates to $r^2\dot\nu=H$. By changing the dependence of $r$ so that $r(t)=r(\nu(t))$ we find $\ddot\nu=\frac d{dt}\frac{H}{r^2}=-2\frac{H}{r^3}r^\prime\dot\nu=-2\frac{H^2}{r^5}r^\prime$ and consequently $\dot r=r^\prime \dot \nu$ and $\ddot r=r^{\prime\prime}\dot\nu^2+r^\prime\ddot\nu=r^{\prime\prime}\frac{H^2}{r^4}-2\frac{H^2}{r^5}{r^\prime}^2$. With this, the remaining equation $\ddot r-r\dot\nu^2+\frac{GM}{r^2}=0$ rewrites as the ordinary differential equation \[\frac{H^2}{r^4}\left(r^{\prime\prime}-2\frac{{r^\prime}^2}{r}-r\right)+\frac{GM}{r^2}=0.\] To solve this equation define the new function $s(\nu):=\frac{1}{r(\nu)}$ so that $r^\prime= -\frac{s^\prime}{s^2}$ and $r^{\prime\prime}=\frac{2s{s^\prime}^2-s^2s^{\prime\prime}}{s^4}$. The latter equation rewrites as \[H^2\left(s^{\prime\prime}+s\right)=GM\] with general solution $s(\nu)=\frac{GM}{H^2}(1+\varepsilon\cos(\nu-\nu_0))$ or \begin{equation}\label{eq:la2} r(\nu)=\frac{H^2}{GM}\frac{1}{1+\varepsilon\cos(\nu-\nu_0)}. \end{equation}

Kepler's first law

Compare the equations \eqref{eq:la2} and \eqref{eq:ell} to see that the orbit is an ellipse with $H=\sqrt{\frac{GM}{a}}\cdot b$.

Kepler's 2^nd law

The area is \[A(t,t_0)=\int_{\nu_0}^{\nu} \frac12 r(\nu)\cdot r(\nu)d \nu=\int_{t_0}^{t} \frac12 r(\nu(u))^2\dot\nu(u)d u.\] Now recall that $r^2\dot\nu=H$ so that $A(t,t_0)=\frac{H}2(t-t_0)$ grows linearly with time.

Kepler's third law

Using \[\mathbf r=a\begin{pmatrix}\cos E-\varepsilon\\ \sqrt{1-\varepsilon^2}\sin E\end{pmatrix} \quad\text{ and } \quad \dot{\mathbf r}=a\dot E\begin{pmatrix}-\sin E\\ \sqrt{1-\varepsilon^2}\cos E\end{pmatrix}\] we find that $H=|\mathbf r\times\dot{\mathbf r}| = a b(1-\varepsilon \cos E) \dot E$, which integrates to $H t= a b(E-\varepsilon\sin E)$ or \begin{equation}\label{eq:Kepler} E-\varepsilon\sin E = \sqrt{\frac{G M}{a^3}} t= \frac{2\pi t}{P}. \end{equation} This is Kepler's equation, where the period $P$ satisfies \[\frac{P^2}{a^3}= \frac{4\pi^2}{GM},\] Kepler's third law. Note as well the relation \[\dot E=\sqrt\frac{GM}{a^3}\frac{1}{1-\varepsilon\cos E}.\]

The velocity vector

We finally notice that \[\dot{\mathbf r}=\sqrt{\frac{G M}{a}}\frac{1}{1-\varepsilon\cos E}\begin{pmatrix}-\sin E\\\sqrt{1-\varepsilon^2}\cos E\end{pmatrix} =\frac{\sqrt{a G M}}{r}\begin{pmatrix}-\sin E\\\sqrt{1-\varepsilon^2}\cos E\end{pmatrix},\] an explicit expression of the velocity vector. With this and Kepler's equation \eqref{eq:Kepler}, Newton's equation \eqref{eq:Newton} can be verified directly ex post.