SOCSupportFunction is an implementation of ConicBundle::SOCOracle for the minimization of the support function over the second order cone with x0=1, which may be used for Lagrangian relaxation of linear programs over the second order cone. More...
Classes | |
| class | ConicBundle::SOCSupportMinorantExtender |
| Implementation of MinorantExtender for SOCSupportFunction. More... | |
| class | ConicBundle::SOCSupportFunction |
| general purpose implementation of SOCOracle as explained in implemention of a SOCOracle (SOCSupportFunction) More... | |
| class | ConicBundle::SOCSupportModification |
| Collects modifications for SOCSupportFunction for appending, deleting or reassigning variables. More... | |
Detailed Description
SOCSupportFunction is an implementation of ConicBundle::SOCOracle for the minimization of the support function over the second order cone with x0=1, which may be used for Lagrangian relaxation of linear programs over the second order cone.
The class SOCSupportFunction implements a general purpose version of SOCOracle for minimizing the support function
![\[f:\mathbf{R}^n\to\mathbf{R},\quad f(\tilde c)=\max\{\tilde c^\top{1 \choose \bar x}\colon 1\ge\|\bar x\|\}\]](form_298.png)
When adding this function to the solver by MatrixCBsolver::add_function(), one may specify a weight 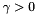 , a ConicBundle::FunctionTask, and an AffineFunctionTransformation
, a ConicBundle::FunctionTask, and an AffineFunctionTransformation 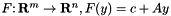 for given
for given 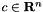 and
and 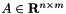 . Depending on the ConicBundle::FunctionTask, the solver actually minimizes the following:
. Depending on the ConicBundle::FunctionTask, the solver actually minimizes the following:
- FunctionTask::ObjectiveFunction
![\[ f_{\gamma,F}(y)=\gamma f(F(y))=\gamma\max\{(c+Ay)^\top {1 \choose \bar x}\colon 1\ge\|\bar x\|\},\]](form_299.png)
If in setting up the groundset within MatrixCBSolver the 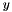 variables are introduced with a linear cost vector
variables are introduced with a linear cost vector 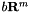 and appropriate sign constraints, this corresponds to Lagrangian relaxation of the linear constraints in the second order cone program
and appropriate sign constraints, this corresponds to Lagrangian relaxation of the linear constraints in the second order cone program
![\[ \mbox{maximize } c^\top x \mbox{ subject to } A^\top x \begin{array}{c}\le\\=\\\ge\end{array} b, x={x_0 \choose \bar x}\mbox{ with }\|\bar x\|\le x_0=\gamma \]](form_300.png)
- FunctionTask::ConstantPenaltyFunction
![\[ f^+_{\gamma,F}(y)=\gamma\max\{0,f(F(y))\},\]](form_263.png)
or, as above in the Lagrangean relaxation setting
![\[ \mbox{maximize } c^\top x \mbox{ subject to } A^\top x \begin{array}{c}\le\\=\\\ge\end{array} b, x={x_0 \choose \bar x}\mbox{ with }\|\bar x\|\le x_0\le\gamma \]](form_301.png)
- FunctionTask::AdaptivePenaltyFunction
![\[ f^+_{\infty,F}(y)=\gamma\max\{0,f(F(y))\}\mbox{ with }\gamma\to \infty,\]](form_302.png)
or, as above in the Lagrangean relaxation setting
![\[ \mbox{maximize } c^\top x \mbox{ subject to } A^\top x \begin{array}{c}\le\\=\\\ge\end{array} b, x={x_0 \choose \bar x}\mbox{ with }\|\bar x\|\le x_0\le\gamma\mbox{ and }\gamma\to \infty \]](form_303.png)
The standard use of a SOCSupportFunction is to initialize it on construction with dimension>=1 and then to add this function to the MatrixCBSolver. If dynamic changes to this SOCSupportFunction are required afterwards (only adding, deleting, rearranging coordinates with index != 0 is allowed), use the class ConicBundle::SOCSupportModification within the corresponding problem modification routines of the MatrixCBSolver interface.
The minorant generated for the input cost vector 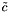 is a maximizing element of the second order cone, so it is itself the basic primal data and no extra primal data is needed.
is a maximizing element of the second order cone, so it is itself the basic primal data and no extra primal data is needed.
For facilitating input and output, SOCSupportFunction offers
- SOCSupportFunction::print_problem_data() that outputs the full function description so that it can be read again by read_problem_data
- SOCSupportFunction::read_problem_data() reads the problem data as output by print_problem_data()
- SOCSupportFunction::set_out() and SOCSupportFunction::set_cbout() work as described in ConicBundle::CBout
 1.8.13
1.8.13