The Full Conic Bundle method solver invoked by ConicBundle::MatrixCBSolver(), it uses a separate cutting model for each function. More...
#include <MatrixCBSolver.hxx>
Public Member Functions | |
| MatrixCBSolver (std::ostream *out=0, int print_level=0) | |
| default constructor allows to set output level options from start (see also set_out()) | |
| MatrixCBSolver (const CBout *cb, int incr=0) | |
| constructor for setting output options depending on existing CBout objects | |
Initialization | |
| void | clear () |
| Clears all data structures and problem information but keeps ouptut settings and algorithmic parameter settings. | |
| void | set_defaults () |
| Sets default values for algorithmic parameters that are not function specific (e.g., relative precision, weight and weight bounds for the augmentedproblem, etc.) | |
| int | init_problem (int dim, const CH_Matrix_Classes::Matrix *lbounds=0, const CH_Matrix_Classes::Matrix *ubounds=0, const CH_Matrix_Classes::Matrix *startval=0, const CH_Matrix_Classes::Matrix *costs=0, CH_Matrix_Classes::Real offset=0.) |
| Initializes the problem by setting up the design space (the dimension and possibly box constraints on the variables) More... | |
| int | add_function (FunctionObject &function, CH_Matrix_Classes::Real fun_factor=1., FunctionTask fun_task=ObjectiveFunction, AffineFunctionTransformation *aft=0, bool argument_list_may_change_dynamically=false) |
| Adds a function, typically derived from ConicBundle::FunctionOracle. If the dimension does not match the current one, specify an affine function transformation to map the current ground set to the argument of the function. More... | |
| int | set_lower_bound (int i, double lb) |
| Sets lower bound for variable i, use ConicBundle::CB_minus_infinity for unbounded from below. More... | |
| int | set_upper_bound (int i, double ub) |
| Sets upper bound for variable i, use ConicBundle::CB_plus_infinity for unbounded from below. More... | |
| int | append_variables (int n_append, const CH_Matrix_Classes::Matrix *lbounds=0, const CH_Matrix_Classes::Matrix *ubounds=0, const CH_Matrix_Classes::Sparsemat *constraint_columns=0, const CH_Matrix_Classes::Matrix *startval=0, const CH_Matrix_Classes::Matrix *costs=0, const FunObjModMap *affected_functions_with_modifications=0) |
| Append new variables (always in last postions in this order). More... | |
| int | delete_variables (const CH_Matrix_Classes::Indexmatrix &delete_indices, CH_Matrix_Classes::Indexmatrix &map_to_old, const FunObjModMap *affected_functions_with_modifications=0) |
| Deletes variables corresponding to the specified indices. More... | |
| int | reassign_variables (const CH_Matrix_Classes::Indexmatrix &assign_new_from_old, const FunObjModMap *affected_functions_with_modifications=0) |
| Reassigns variables to new index positions by mapping to position i the variable that previously had index assign_new_from_old[i]. More... | |
| int | append_constraints (CH_Matrix_Classes::Integer append_n_rows, const CH_Matrix_Classes::Sparsemat *append_rows=0, const CH_Matrix_Classes::Matrix *append_rhslb=0, const CH_Matrix_Classes::Matrix *append_rhsub=0) |
append 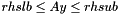 as linear constraints on the groundset variables as linear constraints on the groundset variables 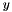 . . 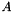 has append_n_rows new rows with coefficients given in append_rows (if NULL, use default value), lower bounds append_rhslb (if NULL use default) and upper bounds append_rhsub (if NULL use default) More... has append_n_rows new rows with coefficients given in append_rows (if NULL, use default value), lower bounds append_rhslb (if NULL use default) and upper bounds append_rhsub (if NULL use default) More... | |
Basic algorithmic routines and parameters | |
| int | solve (int maxsteps=0, bool stop_at_descent_steps=false) |
| solves or does a prescribed number of iterations More... | |
| int | termination_code () const |
| Returns the termination code of the bundle algorithm for the latest descent step. More... | |
| std::ostream & | print_termination_code (std::ostream &out) |
| Outputs a text version of termination code, see termination_code(). More... | |
| double | get_objval () const |
| Returns the objective value resulting from last descent step (initially undefined). If no problem modification routines were called since then, it is the objective value at the point returned by get_center(). | |
| int | get_center (CH_Matrix_Classes::Matrix ¢er) const |
| Returns the next center point that was produced by the latest call to solve (in some problem modification routines the center point may be updated immediately, in others the center point will be corrected automatically directly before starting the next descent step and its values may be infeasible till then). More... | |
| double | get_sgnorm () const |
| Returns Euclidean norm of the latest aggregate subgradient. | |
| int | get_subgradient (CH_Matrix_Classes::Matrix &subgradient) const |
| Returns the latest aggregate subgradient (of the entire problem with groundset as provided by the solver) More... | |
| double | get_cutval () const |
| Returns the cutting model value resulting from last call to solve() (initially undefined). | |
| double | get_candidate_value () const |
| Returns the objective value computed in the last step of solve(), independent of whether this was a descent step or a null step (initially undefined). More... | |
| int | get_candidate (CH_Matrix_Classes::Matrix ¢er) const |
| Returns the last point, the "candidate", at which the function was evaluated in solve(). More... | |
Advanced algorithmic routines and parameters | |
| int | set_term_relprec (const double term_relprec) |
| Sets the relative precision requirements for successful termination (default 1e-5). More... | |
| int | set_new_center_point (const CH_Matrix_Classes::Matrix ¢er_point) |
| Set the starting point/center that will be used in the next call to solve(). Each call to this routine causes an immediate evaluation of all oracles. More... | |
| int | get_function_status (const FunctionObject &function) const |
| Returns the return value of the latest evaluation call to this function. | |
| int | get_approximate_slacks (CH_Matrix_Classes::Matrix &) const |
| Returns the multipliers for the box constraints on the design variables; in Lagrangean relaxation they may be interpreted as primal slacks for inequality constraints. More... | |
| const PrimalData * | get_approximate_primal (const FunctionObject &function) const |
| returns the current approximate primal solution corresponding to the aggregate subgradient of the specified function. More... | |
| const PrimalData * | get_center_primal (const FunctionObject &function) const |
| Returns the primal solution corresponding to the best epsilon subgradient returned in the evaluation of the specified function at the current center point. If no primal data is availalbe, the function returns NULL. More... | |
| const PrimalData * | get_candidate_primal (const FunctionObject &function) const |
| Returns the primal solution corresponding to the best epsilon subgradient returned in the evaluation of the specified function at the point get_candidate. If no primal data is availalbe, the function returns NULL. More... | |
| int | set_sumbundle (bool use_sumbundle, int n_local_models=-1, const BundleParameters *bundle_parameters=0, int strategy=1) |
| Starts/ends the use of a common SumBundle of the given bundle_size with a heuristic rule for selecting up to n_local_models in each bundle iteration. More... | |
| int | set_max_modelsize (int max_modelsize, const FunctionObject *function=0) |
| Sets the maximum number of subgradients used in forming the cutting model of the specified function. More... | |
| int | set_max_bundlesize (int max_bundlesize, const FunctionObject *function=0) |
| Sets the maximum number of subgradients stored for use in forming the model or determining scaling information, it must be as least as large as max_modelsize (and is increased to this if not) More... | |
| int | set_bundle_parameters (const BundleParameters ¶ms, const FunctionObject *function=0) |
| Sets the maximum bundlesize and the maximum number of new subgradients added in a bundle update of the cutting model for the specified function. The meaning of this routine may differ from standard for predefined special functions with special bundle types. More... | |
| const BundleParameters * | get_bundle_parameters (const FunctionObject *function=0) const |
| Retrieves current bundle parameters (not the actual size in use!) as set for the cutting model of the specified function. More... | |
| int | set_sumbundle_parameters (const SumBundleParametersObject ¶ms, const FunctionObject *function=0) |
| Specifies the behavior of the model (of the specified function) concerning requests to join or start a SumBundle that subsumes several models instead of providing a separate model for each funciton. More... | |
| const BundleData * | get_bundle_data (const FunctionObject *function=0) const |
| Returns all current bundle data of the cutting model of the specified function. More... | |
| int | reinit_function_model (const FunctionObject *function=0) |
| Clears cutting model, subgradients and stored function values for the specified function (but only for the given one, not recursively) More... | |
| int | clear_aggregates (const FunctionObject *function=0) |
| Clears the aggregate parts of the cutting model of this function (but only for the given one, not recursively) More... | |
| int | call_primal_extender (const FunctionObject &function, PrimalExtender &primal_extender) |
| Asks function to call primal_extender for each of its primal objects (see also FunctionOracle::evaluate() ) More... | |
| double | get_last_weight () const |
| Returns the current weight for the quadratic term in the augmented subproblem (may be interpreted as 1./step_size or 1./trustregion-radius). | |
| double | get_next_weight () const |
| Returns the next weight for the quadratic term in the augmented subproblem suggested by the internal weight updating heuristic. | |
| int | set_next_weight (const double weight) |
| Sets the weight (>0) to be used in the quadratic term of the next augmented subproblem (may be interpreted as 1./step_size or 1./trustregion-radius). More... | |
| int | set_min_weight (const double min_weight) |
| Sets a lower bound on the weight for the quadratic term of the augmented subproblem. More... | |
| int | set_max_weight (const double max_weight) |
| Sets an upper bound on the weight for the quadratic term of the augmented subproblem. More... | |
| int | set_weight_update (BundleWeight *bw) |
| Replaces the internal update routine for choosing the weight used in the proximal term; input NULL reinstalls the default routine. More... | |
| int | adjust_multiplier (void) |
| Adjusts on all conic functions the penalty parameter for conic violations to twice the trace of the primal approximation. More... | |
| int | set_variable_metric (int do_variable_metric) |
| Use a variable metric heuristic or switch off general metrics alltogether. (variable metric resets the quadratic term e.g. to some diagonal matrix, switching it off resets the quadratic term to the identity times the weight) More... | |
| int | set_prox (BundleProxObject *proxp) |
| For variable metric install the BundleProxObject pointed to; the object is passed to the solver who will delete it on termination or when replaced. More... | |
| void | set_active_bounds_fixing (bool allow_fixing) |
| If set to true (the default is false), variables may be fixed automatically to active bounds if these are strongly active (i.e., the corresponding multipliers are big) and the center values are also right on these bounds already. More... | |
| void | clear_fail_counts (void) |
| clears all fail counts on numerical function oder model failures, may be useful if this caused premature termination. More... | |
| void | set_eval_limit (CH_Matrix_Classes::Integer eval_limit) |
| Sets an upper bound on the number of calls to the oracle (use negative numbers for no limit). More... | |
| void | set_inner_update_limit (CH_Matrix_Classes::Integer update_limit) |
| Set an upper bound on the number of inner updates for the cutting model with primal slacks within one null step (use negative numbers for no limit). More... | |
| void | set_time_limit (CH_Matrix_Classes::Integer time_limit) |
| Set an upper bound on the number of seconds (user time, use negative numbers for no limit) More... | |
| int | set_qp_solver (QPSolverParametersObject *qpparams, QPSolverObject *newqpsolver=0) |
Look up basic paramaters (dimension, number of functions, ...) | |
| int | get_dim () const |
| Returns the current dimension of the design space/argument or -1 if no dimension is set. | |
| int | get_n_functions () const |
| Returns the current number of functions in the problem. | |
| int | get_n_oracle_calls () const |
| Returns the number of function evaluations. | |
| int | get_n_descent_steps () const |
| Returns the number of function descent setps. | |
| int | get_n_inner_iterations () const |
| Returns the number of inner iterations of the bundle method. | |
| int | get_n_inner_updates () const |
| Returns the number of inner multiplier updates for the box constraints. | |
| bool | get_descent_step () const |
| returns true if the last evaluation of the last call to solve() resulted in a descent step More... | |
| bool | get_null_step () const |
| returns true if the last evaluation of the last call to solve() resulted in a null step More... | |
| int | get_costs (CH_Matrix_Classes::Matrix &costs) const |
| If a linear cost vector was specified, costs will hold these values, otherwise the vector is initialized to zero (for the current dimension) | |
| const CH_Matrix_Classes::Matrix * | get_lbounds () const |
| Returns a pointer to the vector of lower bounds or null if there is no such vector. | |
| const CH_Matrix_Classes::Matrix * | get_ubounds () const |
| Returns a pointer to the vector of upper bounds or null if there is no such vector. | |
| const CH_Matrix_Classes::Indexmatrix * | get_fixed_active_bounds () const |
| Returns NULL or (iff active bound fixing is turned on in set_active_bounds_fixing()) the indicator vector of variables temporarily fixed to the center value due to significantly positive multipliers for the box constraints. More... | |
| BundleProxObject * | get_prox () const |
| Returns the pointer to the current prox term of the bundle solver. | |
| bool | pending_oracle_modification (const FunctionObject &function, CH_Matrix_Classes::Integer &old_dim, CH_Matrix_Classes::Integer &new_dim, CH_Matrix_Classes::Integer &append_dim, const CH_Matrix_Classes::Indexmatrix *&map_to_old, const CH_Matrix_Classes::Indexmatrix *&deleted_indices, const CH_Matrix_Classes::Indexmatrix *&new_indices, const OracleModification *&oracle_modification) const |
| returns true if for function some modifications are pending, the arguments give information on these | |
Output | |
| void | set_out (std::ostream *out=0, int print_level=1) |
| Specifies the output level (out==NULL: no output at all, out!=NULL and level=0: errors and warnings, level>0 increasingly detailed information) More... | |
| std::ostream & | print_line_summary (std::ostream &out) const |
| print a one line summary of important evaluation data | |
| std::ostream & | print_statistics (std::ostream &out) const |
| print a cryptic summary of computation times of important components | |
 Public Member Functions inherited from ConicBundle::CBout Public Member Functions inherited from ConicBundle::CBout | |
| virtual void | set_cbout (const CBout *cb, int incr=-1) |
| Specifies the output level relative to the given CBout class. More... | |
| void | clear_cbout () |
| reset to default settings (out=0,print_level=1) | |
| CBout (const CBout *cb=0, int incr=-1) | |
| calls set_cbout | |
| CBout (std::ostream *outp, int pl=1) | |
| initialize correspondingly | |
| CBout (const CBout &cb, int incr=0) | |
| copy constructor | |
| virtual bool | cb_out (int pl=-1) const |
| Returns true if out!=0 and (pl<print_level), pl<0 should be used for WARNINGS and ERRORS only, pl==0 for usual output. | |
| std::ostream & | get_out () const |
| If cb_out() returned true, this returns the output stream, but it will abort if called with out==0. | |
| std::ostream * | get_out_ptr () const |
| returns the pointer to the output stream | |
| int | get_print_level () const |
| returns the print_level | |
| virtual int | mfile_data (std::ostream &out) const |
| writes problem data to the given outstream | |
Private Member Functions | |
| MatrixCBSolver (const MatrixCBSolver &) | |
| not available, blocked deliberately | |
| MatrixCBSolver & | operator= (const MatrixCBSolver &) |
| not available, blocked deliberately | |
Private Attributes | |
| MatrixCBSolverData * | data_ |
| pointer to internal solver data | |
Detailed Description
The Full Conic Bundle method solver invoked by ConicBundle::MatrixCBSolver(), it uses a separate cutting model for each function.
Minimizes the sum of convex functions that are given via ConicBundle::MatrixFunctionOracle interfaces, see the text explaining the C++ interface for Matrix Classes for a quick overview.
It provides special support for Lagrangean relaxation by generating primal approximate solutions if such information is provided in the function oracles.
Based on these primal approximations it is also possible to implement cutting plane schemes. Routines for adding and deleting corresponding dual variables as well as a framework for extending subgradients in order not to loose the cutting model are available.
Member Function Documentation
◆ add_function()
| int ConicBundle::MatrixCBSolver::add_function | ( | FunctionObject & | function, |
| CH_Matrix_Classes::Real | fun_factor = 1., |
||
| FunctionTask | fun_task = ObjectiveFunction, |
||
| AffineFunctionTransformation * | aft = 0, |
||
| bool | argument_list_may_change_dynamically = false |
||
| ) |
Adds a function, typically derived from ConicBundle::FunctionOracle. If the dimension does not match the current one, specify an affine function transformation to map the current ground set to the argument of the function.
Besides the standard ConicBundle::MatrixFunctionOracle the interface only accepts a few other prespecified derivations of the class FunctionObject that come along with the CH_Matrix_Classes interface (e.g. for semidefinite and second order cones). Functions not derived from these will fail to be added and return a value !=0.
The fun_factor allows to specify a scaling factor for the function. fun_factor must be a strictly positive number.
The ConicBundle::FunctionTask fun_task specifies whether the function is to be used as a an ObjectiveFunction, a ConstantPenaltyFunction with fun_factor as maximum penalty factor, or as an AdaptivePenaltyFunction with fun_factor at initial penalty guess that might be increased or decreased over time.
The AffineFunctionTransformation aft may be used to modify the argument and give an additional affine term (linear term plus offset). For adding an affine term there are several other possibilities, e.g. in init_problem(), so there is no need to do so here. If, however, an existing function implementation requires only some subset of the variables, it is more convenient to supply a corresponding aft instead of reimplementing the function.
argument_list_may_change_dynamically sets a flag on how to treat the function arguments when variables are added or deleted. If the arguments may not change, any changes in the variables are mapped to an adaptation of an internal AffineFunctionTransformation so that the function does not notice the changes in the variables. If arguments may change, the function oracle should be a ModifiableOracleObject and react accordingly to the changes in its ModifiableOracleObject::apply_modification() routine.
- Returns
- 0 on success
- != 0 otherwise
◆ adjust_multiplier()
| int ConicBundle::MatrixCBSolver::adjust_multiplier | ( | void | ) |
Adjusts on all conic functions the penalty parameter for conic violations to twice the trace of the primal approximation.
This routine is only needed for conic function objects such as the nonnegative cone, the second order cone and the semidefinite cone if no good upper bound on the trace of feasible points is known and has to be determined automatically.
If after some time, the trace values settle, the upper bounds on the trace may be way to high and can then be reset with this call.
- Returns
- 0 on success
- != 0 otherwise
◆ append_constraints()
| int ConicBundle::MatrixCBSolver::append_constraints | ( | CH_Matrix_Classes::Integer | append_n_rows, |
| const CH_Matrix_Classes::Sparsemat * | append_rows = 0, |
||
| const CH_Matrix_Classes::Matrix * | append_rhslb = 0, |
||
| const CH_Matrix_Classes::Matrix * | append_rhsub = 0 |
||
| ) |
append 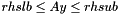 as linear constraints on the groundset variables
as linear constraints on the groundset variables 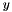 .
.  has append_n_rows new rows with coefficients given in append_rows (if NULL, use default value), lower bounds append_rhslb (if NULL use default) and upper bounds append_rhsub (if NULL use default)
has append_n_rows new rows with coefficients given in append_rows (if NULL, use default value), lower bounds append_rhslb (if NULL use default) and upper bounds append_rhsub (if NULL use default)
- Parameters
-
[in] append_n_rows (Integer) (nonnegative) number of rows to be appended as linear constraints on the ground set [in] append_rows (Sparsemat*) describes the coefficients of the linear constraints; the number of rows must match append_n_rows, the number of columns must match the current dimension of the groundset; if NULL, all coefficients are considered zero. [in] append_rhslb (Matrix*) specifies lower bounds on the values of the constraints; the number of rows must match append_n_rows; if NULL, all coefficients are considered CB_minus_infinity. [in] append_rhsub (Matrix*) specifies upper bound on the values of the constraints; the number of rows must match append_n_rows; if NULL, all coefficients are considered CB_plus_infinity.
- Returns
- 0 on success
- != 0 otherwise
◆ append_variables()
| int ConicBundle::MatrixCBSolver::append_variables | ( | int | n_append, |
| const CH_Matrix_Classes::Matrix * | lbounds = 0, |
||
| const CH_Matrix_Classes::Matrix * | ubounds = 0, |
||
| const CH_Matrix_Classes::Sparsemat * | constraint_columns = 0, |
||
| const CH_Matrix_Classes::Matrix * | startval = 0, |
||
| const CH_Matrix_Classes::Matrix * | costs = 0, |
||
| const FunObjModMap * | affected_functions_with_modifications = 0 |
||
| ) |
Append new variables (always in last postions in this order).
- Attention
- Be sure to include a desription of required changes to your functions via affected_functions_with_modifications
- Parameters
-
[in] n_append (int) number of variables to append (always in last position in the same order) [in] lbounds (const Matrix*) If NULL, all appended variables are considered unbounded below, otherwise lbounds[i] gives the minimum feasible value for variable y[i], use ConicBundle::CB_minus_infinity for unbounded below. [in] ubounds (const Matrix*) If NULL, all appended variables are considered unbounded above, otherwise ubounds[i] gives the maximum feasible value for variable y[i], use ConicBundle::CB_plus_infinity for unbounded above. [in] constraint_columns (const Sparsemat*) This must be NULL unless append_constraints() has been used before for specifying linear constraints on the ground set; if there are constraints, NULL is interpreted as appending zero columns to the constraints, otherwise the the number of rows of the Sparsemant has to match the current number of linear constraints and the number of columns the must equal n_append. [in] startval (const Matrix*) If NULL, the starting values are obtained by projecting zero onto the feasible set given by the lower and upper bounds resulting from the arguments before [in] costs (const Matrix*) Use this in order to specify linear costs on the variables in addition to the functions (may be convenient in Lagrangean relaxation for the right hand side of coupling contsraints); NULL is equivalent to costs zero. [in,out] affected_functions_with_modifications (const FunObjModMap*) If NULL, default actions are performed on all functions. In particular, those admitting dynamic argument changes will get the new variables appended at the end of their argument vector and (eventually) their apply_modification() routines will be called informing them about the groundset changes; for those not admitting changes in their arguments, their corresponding (possibly newly created) affine function transformation will be set up to ignore the new arguments. If !=NULL, for the listed functions (and their parents up to the root function) the default appending action is performed unless their FunctionObjectModification entry gives explicit modification instructions which are then applied instead. For all functions NOT listed in the map and not having modified offsprings their corresponding aft will be set up to ignore the new variables.
- Returns
- 0 on success
- != 0 otherwise
◆ call_primal_extender()
| int ConicBundle::MatrixCBSolver::call_primal_extender | ( | const FunctionObject & | function, |
| PrimalExtender & | primal_extender | ||
| ) |
Asks function to call primal_extender for each of its primal objects (see also FunctionOracle::evaluate() )
If the function is the Lagrangian dual of a primal problem and primal_data returned previous calls to the oracle has now to be updated due to changes in the primal problem – e.g., this may happen in column generation – the call causes updates of all internally stored primal_data objects by calling PrimalExtender::extend on each of these.
- Parameters
-
[in] function (const FunctionObject&) the function added in add_function() [in] primal_extender (PrimalExtender&) the object holding the extension function for primal_data
- Returns
- 0 on success
- 1 if for this function it is not possible to use a primal_extender
- 2 if the primal_extender would be applicable but there is no primal_data
◆ clear_aggregates()
| int ConicBundle::MatrixCBSolver::clear_aggregates | ( | const FunctionObject * | function = 0 | ) |
Clears the aggregate parts of the cutting model of this function (but only for the given one, not recursively)
There should be no need to call this if the modification routines of this interface were used correctly. If, however, the oracle is modified by other means outside this interface, this has to be called whenever the specified function was modified so that the old aggregate subgradients and/or primal generators are no longer valid.
- Parameters
-
[in] function (const FunctionObject&) the function added in add_function()
- Returns
- 0 on success
- != 0 otherwise
◆ clear_fail_counts()
| void ConicBundle::MatrixCBSolver::clear_fail_counts | ( | void | ) |
clears all fail counts on numerical function oder model failures, may be useful if this caused premature termination.
- Returns
- 0 on success
- != 0 otherwise
◆ delete_variables()
| int ConicBundle::MatrixCBSolver::delete_variables | ( | const CH_Matrix_Classes::Indexmatrix & | delete_indices, |
| CH_Matrix_Classes::Indexmatrix & | map_to_old, | ||
| const FunObjModMap * | affected_functions_with_modifications = 0 |
||
| ) |
Deletes variables corresponding to the specified indices.
The indices of the remaining variables are reassigned so that they are consecutive again, the routine returns in map_to_old a vector giving for each new index of these remaining variables the old coordinate.
- Attention
- Be sure to include a desription of required changes to your functions via affected_functions_with_modifications
- Parameters
-
[in] delete_indices (const Indexmatrix&) the entries delete_indices[i] specify the indices of the variables to be deleted [out] map_to_old (Indexmatrix&) after the call, element map_to_old[i] gives the old index (before the call) of the variable that now has index position i. [in] affected_functions_with_modifications (const FunObjModMap*) If NULL, default actions are performed on all functions. In particular, for those admitting dynamic argument changes all those variables will be deleted whose row in a corresponding updated affine function transformation (so after deletion of the columns of the incoming variables) corresponds to the zero map (i.e., offset and matrix row are both zero), furthermore identity transformations will be preserved. For those not admitting changes in their arguments, their corresponding (possibly newly created) affine function transformation will only get the columns deleted, but there will be no row deleltions. If !=NULL, for the listed functions (and their parents up to the root function) the default deletion action is performed unless their FunctionObjectModification entry gives explicit modification instructions which are then applied instead. For all functions NOT listed in the map and not having modified offsprings their corresponding aft will be set up to keep the arguments unchanged.
- Returns
- 0 on success
- != 0 otherwise
◆ get_approximate_primal()
| const PrimalData* ConicBundle::MatrixCBSolver::get_approximate_primal | ( | const FunctionObject & | function | ) | const |
returns the current approximate primal solution corresponding to the aggregate subgradient of the specified function.
PrimalData solutions must have been supplied in all previous calls to evaluate; In this case it returns the current approximate primal solution aggregated alongside with the aggregate subgradient. A primal solution may not be available after addition of constraints, if extension of the aggregate subgradient to the new coordinates failed. If no primal data is availalbe, the function returns NULL.
- Returns
- pointer to the primal data of the aggregate of this function object
- 0 if no primal is available
◆ get_approximate_slacks()
| int ConicBundle::MatrixCBSolver::get_approximate_slacks | ( | CH_Matrix_Classes::Matrix & | ) | const |
Returns the multipliers for the box constraints on the design variables; in Lagrangean relaxation they may be interpreted as primal slacks for inequality constraints.
- Returns
- 0 on success
- != 0 otherwise
◆ get_bundle_data()
| const BundleData* ConicBundle::MatrixCBSolver::get_bundle_data | ( | const FunctionObject * | function = 0 | ) | const |
Returns all current bundle data of the cutting model of the specified function.
This may differ for predefined special functions with derived classes.
- Parameters
-
[in] function if the aggregate subgradient of a particular function is desired, provide the pointer here, otherwise this referrs to the root function (if there is only one function to be optimized over, this is this single function, otherwise it is the sum of functions)
- Returns
- 0 on success
- != 0 otherwise
◆ get_bundle_parameters()
| const BundleParameters* ConicBundle::MatrixCBSolver::get_bundle_parameters | ( | const FunctionObject * | function = 0 | ) | const |
Retrieves current bundle parameters (not the actual size in use!) as set for the cutting model of the specified function.
This may differ for predefined special functions with derived BundleParameter classes.
If the code is asked to optimize over the sum of several functions, it usually does this with a separate model for each function. If there are too many function for this, it may be worth to consider using the SumBundle features. For this see also set_sumbundle_parameters(). If the root function is a sum of functions, passing a SumModelParametersObject here allows to specify how many local models should be kept by SumModelParametersObject::set_max_local_models() and how these should be selected. A possible implementation for this is given in SumModelParameters.
- Parameters
-
[in] function if the aggregate subgradient of a particular function is desired, provide the pointer here, otherwise this referrs to the root function (if there is only one function to be optimized over, this is this single function, otherwise it is the sum of functions)
- Returns
- 0 on success
- != 0 otherwise
◆ get_candidate()
| int ConicBundle::MatrixCBSolver::get_candidate | ( | CH_Matrix_Classes::Matrix & | center | ) | const |
Returns the last point, the "candidate", at which the function was evaluated in solve().
If this evaluation lead to a descent step, it is the same point as in get_center().
- Returns
- 0 on success
- != 0 otherwise
◆ get_candidate_primal()
| const PrimalData* ConicBundle::MatrixCBSolver::get_candidate_primal | ( | const FunctionObject & | function | ) | const |
Returns the primal solution corresponding to the best epsilon subgradient returned in the evaluation of the specified function at the point get_candidate. If no primal data is availalbe, the function returns NULL.
- Returns
- pointer to the primal data of the minorant returned on evaluation of this function object at the current candidate
- 0 if no primal is available
◆ get_candidate_value()
| double ConicBundle::MatrixCBSolver::get_candidate_value | ( | ) | const |
Returns the objective value computed in the last step of solve(), independent of whether this was a descent step or a null step (initially undefined).
If no problem modification routines were called since then, it is the objective value at the point returned by get_candidate(). If this last evaluation led to a descent step, then it is the same value as in get_objval().
◆ get_center()
| int ConicBundle::MatrixCBSolver::get_center | ( | CH_Matrix_Classes::Matrix & | center | ) | const |
Returns the next center point that was produced by the latest call to solve (in some problem modification routines the center point may be updated immediately, in others the center point will be corrected automatically directly before starting the next descent step and its values may be infeasible till then).
- Returns
- 0 on success
- != 0 otherwise
◆ get_center_primal()
| const PrimalData* ConicBundle::MatrixCBSolver::get_center_primal | ( | const FunctionObject & | function | ) | const |
Returns the primal solution corresponding to the best epsilon subgradient returned in the evaluation of the specified function at the current center point. If no primal data is availalbe, the function returns NULL.
- Returns
- pointer to the primal data of the minorant returned on evaluation of this function object at the current center
- 0 if no primal is available
◆ get_descent_step()
| bool ConicBundle::MatrixCBSolver::get_descent_step | ( | ) | const |
returns true if the last evaluation of the last call to solve() resulted in a descent step
Mind: if there was no (succesdful) evaluation, neither get_descent_step() nor get_null_step() will return true;
◆ get_fixed_active_bounds()
| const CH_Matrix_Classes::Indexmatrix* ConicBundle::MatrixCBSolver::get_fixed_active_bounds | ( | ) | const |
Returns NULL or (iff active bound fixing is turned on in set_active_bounds_fixing()) the indicator vector of variables temporarily fixed to the center value due to significantly positive multipliers for the box constraints.
A variable gets fixed to the bound only if the center is already a the bound and in some iteration the dual variables to the bound constraint indicate that the bound is strongly active also for the candidate. Of course this migh just hold for one candidate and there is no guarantee that the bound is also strongly active in an optimal solution. Thus, this mainly a heuristic to eliminate less important variables quickly from entering the subproblem.
◆ get_null_step()
| bool ConicBundle::MatrixCBSolver::get_null_step | ( | ) | const |
returns true if the last evaluation of the last call to solve() resulted in a null step
Mind: if there was no (successful) evaluation, neither get_descent_step() nor get_null_step() will return true;
◆ get_subgradient()
| int ConicBundle::MatrixCBSolver::get_subgradient | ( | CH_Matrix_Classes::Matrix & | subgradient | ) | const |
Returns the latest aggregate subgradient (of the entire problem with groundset as provided by the solver)
- Returns
- 0 on success
- != 0 otherwise
◆ init_problem()
| int ConicBundle::MatrixCBSolver::init_problem | ( | int | dim, |
| const CH_Matrix_Classes::Matrix * | lbounds = 0, |
||
| const CH_Matrix_Classes::Matrix * | ubounds = 0, |
||
| const CH_Matrix_Classes::Matrix * | startval = 0, |
||
| const CH_Matrix_Classes::Matrix * | costs = 0, |
||
| CH_Matrix_Classes::Real | offset = 0. |
||
| ) |
Initializes the problem by setting up the design space (the dimension and possibly box constraints on the variables)
Clears all data structures and sets the dimension @ m for a new problem. for solving min_{y in R^m} f_0(y) + f_1(y) + ... Box constraints may be specified for y. (The functions f_i must be added by add_function()).
Lower and/or upper bounds must be speicified for all variables or for none of them. To specify no bounds at all, give Null pointers. Otherwise use ConicBundle::CB_minus_infinity for unbounded below and ConicBundle::CB_plus_infinity for unbounded above. For NULL pointers, unbounded will be used as default for all variables. Specifying bounds selectively is also possible by set_lower_bound() or set_upper_bound(). For further constraints see append_constraints().
- Parameters
-
[in] dim (int) the dimension of the argument/design space/the number of Lagrange multipliers [in] lbounds (const Matrix*) If NULL, all variables are considered unbounded below, otherwise lbounds[i] gives the minimum feasible value for variable y[i], use ConicBundle::CB_minus_infinity for unbounded below. [in] ubounds (const Matrix*) If NULL, all variables are considered unbounded above, otherwise ubounds[i] gives the maximum feasible value for variable y[i], use ConicBundle::CB_plus_infinity for unbounded above. [in] startval (const Matrix*) If NULL, the starting values are obtained by projecting zero onto the feasible set given by the lower and upper bounds resulting from the arguments before [in] costs (const Matrix*) Use this in order to specify linear costs on the variables in addition to the functions (may be convenient in Lagrangean relaxation for the right hand side of coupling contsraints); NULL is equivalent to costs zero. [in] offset (Real) Use this in order to specify linear costs on the variables in addition to the functions (may be convenient in Lagrangean relaxation for the right hand side of coupling contsraints); NULL is equivalent to costs zero.
- Returns
- 0 on success
- != 0 otherwise
◆ print_termination_code()
| std::ostream& ConicBundle::MatrixCBSolver::print_termination_code | ( | std::ostream & | out | ) |
Outputs a text version of termination code, see termination_code().
- Returns
- 0 on success
- != 0 otherwise
◆ reassign_variables()
| int ConicBundle::MatrixCBSolver::reassign_variables | ( | const CH_Matrix_Classes::Indexmatrix & | assign_new_from_old, |
| const FunObjModMap * | affected_functions_with_modifications = 0 |
||
| ) |
Reassigns variables to new index positions by mapping to position i the variable that previously had index assign_new_from_old[i].
Old variables, that are not mapped to any position will be deleted. It is not allowed to generate several copies of old variables.
- Attention
- Be sure to include a desription of required changes to your functions via affected_functions_with_modifications
- Parameters
-
[in] assign_new_from_old (const IVector&) entry assign_new_from_old[i] specifies the old index of the variable, that has to be copied to index position i. [in] affected_functions_with_modifications (const FunObjModMap*) If NULL, default actions are performed on all functions. In particular, for those admitting dynamic argument changes all those variables will be deleted whose row in a corresponding updated affine function transformation (so after mapping the columns of the incoming variables) correspond to the zero map (i.e., offset and matrix row are both zero); furthermore, if the transformation was the identity to start with, this will be preserved by mapping the arguments in the same way. For those not admitting changes in their arguments, their corresponding (possibly newly created) affine function transformation will only get the columns mapped, but there will be no row deleltions. If !=NULL, for the listed functions (and their parents up to the root function) the default deletion action is performed unless their FunctionObjectModification entry gives explicit modification instructions which are then applied instead. For all functions NOT listed in the map and not having modified offsprings their corresponding aft will be set up to keep the arguments unchanged.
- Returns
- 0 on success
- != 0 otherwise
◆ reinit_function_model()
| int ConicBundle::MatrixCBSolver::reinit_function_model | ( | const FunctionObject * | function = 0 | ) |
Clears cutting model, subgradients and stored function values for the specified function (but only for the given one, not recursively)
There should be no need to call this if the modification routines of this interface were used correctly. If, however, the oracle is modified by other means outside this interface, this has to be called whenever the specified function was modified so that the old subgradients and/or primal generators are no longer valid.
- Parameters
-
[in] function if the aggregate subgradient of a particular function is desired, provide the pointer here, otherwise this referrs to the root function (if there is only one function to be optimized over, this is this single function, otherwise it is the sum of functions)
- Returns
- 0 on success
- != 0 otherwise
◆ set_active_bounds_fixing()
| void ConicBundle::MatrixCBSolver::set_active_bounds_fixing | ( | bool | allow_fixing | ) |
If set to true (the default is false), variables may be fixed automatically to active bounds if these are strongly active (i.e., the corresponding multipliers are big) and the center values are also right on these bounds already.
The coordinates to be fixed are redetermined in each call following a descent step or a change of the function. An indicator vector of the variables fixed during the last call can be obtained via the routine get_fixed_active_bounds().
Setting this value to true might improve the performance of the algorithm in some instances but there is no convergence theory. It might be particularly helpful within Lagrangian relaxation if a primal cutting plane approach is used and non-tight inequalities should be eliminated quickly (fixing then indicates large primal slack values as these are the dual variables to the bounds on the Lagrange mulitpliers). Furthermore, if the value of a variable is fixed to zero, the variable can typically be deleted without affecting the validity of the current cutting model and function values.
- Parameters
-
[in] allow_fixing (bool)
- Returns
- 0 on success
- != 0 otherwise
◆ set_bundle_parameters()
| int ConicBundle::MatrixCBSolver::set_bundle_parameters | ( | const BundleParameters & | params, |
| const FunctionObject * | function = 0 |
||
| ) |
Sets the maximum bundlesize and the maximum number of new subgradients added in a bundle update of the cutting model for the specified function. The meaning of this routine may differ from standard for predefined special functions with special bundle types.
- Parameters
-
[in] params (const BundleParameters&) some update parameters for the cutting model, see e.g. ConicBundle::BundleParameters [in] function if the aggregate subgradient of a particular function is desired, provide the pointer here, otherwise this referrs to the root function (if there is only one function to be optimized over, this is this single function, otherwise it is the sum of functions)
- Returns
- 0 on success
- != 0 otherwise
◆ set_eval_limit()
| void ConicBundle::MatrixCBSolver::set_eval_limit | ( | CH_Matrix_Classes::Integer | eval_limit | ) |
Sets an upper bound on the number of calls to the oracle (use negative numbers for no limit).
If this number is reached, the algorithm will terminate independently of whether the last step was a descent or a null step. A negative number will be interepreted as no limit.
- Parameters
-
[in] eval_limit (Integer)
- Returns
- 0 on success
- != 0 otherwise
◆ set_inner_update_limit()
| void ConicBundle::MatrixCBSolver::set_inner_update_limit | ( | CH_Matrix_Classes::Integer | update_limit | ) |
Set an upper bound on the number of inner updates for the cutting model with primal slacks within one null step (use negative numbers for no limit).
A negative number will be interepreted as no limit, i.e., the updates will be done till a certain precision of the cutting model is achieved.
- Parameters
-
[in] update_limit (Integer)
- Returns
- 0 on success
- != 0 otherwise
◆ set_lower_bound()
| int ConicBundle::MatrixCBSolver::set_lower_bound | ( | int | i, |
| double | lb | ||
| ) |
Sets lower bound for variable i, use ConicBundle::CB_minus_infinity for unbounded from below.
The algorithm may have to adapt the center point aftwards. In this case the old function values will be marked as outdated and will be recomputed at the next call to e.g. solve().
- Returns
- 0 on success
- != 0 otherwise
◆ set_max_bundlesize()
| int ConicBundle::MatrixCBSolver::set_max_bundlesize | ( | int | max_bundlesize, |
| const FunctionObject * | function = 0 |
||
| ) |
Sets the maximum number of subgradients stored for use in forming the model or determining scaling information, it must be as least as large as max_modelsize (and is increased to this if not)
The meaning of this routine may differ from standard for predefined special functions with special bundle types.
- Parameters
-
[in] max_bundlesize (int) maximum number of subgradients stored for use in forming the model [in] function if the aggregate subgradient of a particular function is desired, provide the pointer here, otherwise this referrs to the root function (if there is only one function to be optimized over, this is this single function, otherwise it is the sum of functions)
- Returns
- 0 on success
- != 0 otherwise
◆ set_max_modelsize()
| int ConicBundle::MatrixCBSolver::set_max_modelsize | ( | int | max_modelsize, |
| const FunctionObject * | function = 0 |
||
| ) |
Sets the maximum number of subgradients used in forming the cutting model of the specified function.
Quite often a very small model, e.g., 2, yields very fast iterations and good progress in time (sometimes at the cost of more evaluations). By limited numerical experience, a significant reduction in the number of evaluations can only be expected if the bundle is large enough to wrap the function rather tightly. Quite frequently, unfortunately, this entails that solving the quadratic subproblems is more expensive than function evaluation.
The meaning of this routine may differ from standard for predefined special functions with special bundle types.
- Parameters
-
[in] max_modelsize (int) maximum number of subgradients to be used in forming the cutting model [in] function if the aggregate subgradient of a particular function is desired, provide the pointer here, otherwise this referrs to the root function (if there is only one function to be optimized over, this is this single function, otherwise it is the sum of functions)
- Returns
- 0 on success
- != 0 otherwise
◆ set_max_weight()
| int ConicBundle::MatrixCBSolver::set_max_weight | ( | const double | max_weight | ) |
Sets an upper bound on the weight for the quadratic term of the augmented subproblem.
Nonpositive values indicate no bound. The new value shows its effect only at first dynamic change of the weight.
- Parameters
-
[in] max_weight (double)
- Returns
- 0 on success
- != 0 otherwise
◆ set_min_weight()
| int ConicBundle::MatrixCBSolver::set_min_weight | ( | const double | min_weight | ) |
Sets a lower bound on the weight for the quadratic term of the augmented subproblem.
Nonpositive values indicate no bound. The new value shows its effect only at first dynamic change of the weight.
- Parameters
-
[in] min_weight (double)
- Returns
- 0 on success
- != 0 otherwise
◆ set_new_center_point()
| int ConicBundle::MatrixCBSolver::set_new_center_point | ( | const CH_Matrix_Classes::Matrix & | center_point | ) |
Set the starting point/center that will be used in the next call to solve(). Each call to this routine causes an immediate evaluation of all oracles.
- Returns
- 0 on success
- != 0 otherwise
◆ set_next_weight()
| int ConicBundle::MatrixCBSolver::set_next_weight | ( | const double | weight | ) |
Sets the weight (>0) to be used in the quadratic term of the next augmented subproblem (may be interpreted as 1./step_size or 1./trustregion-radius).
Independent of whether the weight violates current min- and max-bounds set in set_min_weight() and set_max_weight(), the next model will be computed for this value. Thereafter, however, it will be updated as usual; in particular, it may be truncated by min and max bounds immediately after the first subproblem.
In order to guarantee a constant weight (e.g. 1 is frequently a reasonable choice if the automatic default heuristic performs poorly), set the min and max bounds to the same value, too.
- Parameters
-
[in] weight (double)
- Returns
- 0 on success
- != 0 otherwise
◆ set_out()
|
virtual |
Specifies the output level (out==NULL: no output at all, out!=NULL and level=0: errors and warnings, level>0 increasingly detailed information)
- Parameters
-
[in] out (std::ostream*) direct all output to (*out). If out==NULL, there will be no output at all. [in] print_level (int)
Output levels for print_level:
- 0 ... no output except for errors and warnings
- 1 ... line summary after each descent step
- >1 ... undocumented and increasingly detailed log information. These higher levels should only be used if requested for debugging purposes.
Example for level 1:
00:00:00.00 endit 1 1 1 563. 563. 39041.188 39043.162 00:00:00.00 endit 2 2 2 563. 559. 38488.165 38490.200 00:00:00.00 endit 3 3 3 56.3 555. 33014.533 33211.856 00:00:00.00 endit 4 4 4 5.63 517. -14306.459 2738.0343 00:00:00.00 endit 5 5 5 4.04 148. -2692.1131 2.2150883 00:00:00.00 endit 6 6 6 4.01 1.29 1.7908952 2.0000581 00:00:00.00 endit 7 7 7 3.95 0.0213 1.9999387 2.0000000 00:00:00.00 _endit 8 8 8 3.95 2.94e-05 2.0000000 2.0000000 Column 1 2 3 4 5 6 7 8 9
- Column 1: computation time in hh:mm:ss.dd,
- Column 2: "endit" is convenient for grep and stands for "end of iteration". Iterations with termination_code()!=0 are marked with "_endit".
- Column 3: number of descent steps
- Column 4: number of descent and null steps. Up to initialization calls and reevaluations, this is the number of evaluation calls to the function oracles from within the bundle method. In the example all calls led to descent steps.
- Column 5: number of innermost iterations. It differs from column 5 only in the case of variables with bounds in which case it gives the number of updates of the multipliers for the bounds (or primal slacks in Lagrangean relaxation). Exceedingly high numbers in this column indicate that some variables are constantly at their bounds and it might be possible to improve convergence by deleting them (i.e. set them as constants to this bound and remove the variable).
- Column 6: the weight of the quadratic term in the augmented problem.
- Column 7: the norm of the aggregate subgradient. If it is small, say below 0.1, then mostly this is good indication that the objective value is close to optimal.
- Column 8: the value of the cutting model in the last candidate point. It is always a lower bound on the true function value in this point
- Column 9: the objective value in the latest point that led to a descent step, i.e., the point returend by get_center(). Whenever termination_code() returns 0 this is also the objective value of the latest evaluation call to the function oracles and the value in the center point of the next iteration.
Reimplemented from ConicBundle::CBout.
◆ set_prox()
| int ConicBundle::MatrixCBSolver::set_prox | ( | BundleProxObject * | proxp | ) |
For variable metric install the BundleProxObject pointed to; the object is passed to the solver who will delete it on termination or when replaced.
- Parameters
-
[in] proxp (BundleProxObject*) replace the current BundleProxObject by this object on the heap; NULL is allowed and results in the default choice; the object pointed to will be deleted by the solver
- Returns
- 0 on success
- != 0 otherwise
◆ set_sumbundle()
| int ConicBundle::MatrixCBSolver::set_sumbundle | ( | bool | use_sumbundle, |
| int | n_local_models = -1, |
||
| const BundleParameters * | bundle_parameters = 0, |
||
| int | strategy = 1 |
||
| ) |
Starts/ends the use of a common SumBundle of the given bundle_size with a heuristic rule for selecting up to n_local_models in each bundle iteration.
If the function is the sum of many functions, having a local model for every one of them may result in a huge quadratic subproblem. It may then be better to form a common model of most of the functions, where a heuristic dynamically selects a few of the functions, for which a local model seems worth while. Whether such a common model should be used, how many subgradients it should contain, and how many local models are to be selected at most are the parameters set here.
Setting these parameters only has an effect if bundle models of functions are present. If further functions are added later, the call should be repeated.
This interface provides a simpler access to the SumBundle features by using some default parameter choices that could be set separately in set_bundle_parameters() and set_sumbundle_parameters() in a refined way.
- Parameters
-
[in] use_sumbundle (bool) use value true to switch the sumbundle on, use value false to switch it off [in] n_local_models (int) upper bound on the number of local models to be used on top of the sumbundle's model, negative values correspond to no upper bound and all functions may have local models [in] bundle_parameters (const BundleParameters*) the maximum number of subgradients to be used in forming the SumBundle model, values <=1 are set to 2; [in] strategy (int) this is currently in experimental stage and allows to choose among some internal sumbundle strategies (currently 0,1,2,11 are available)
- Returns
- 0 on success
- != 0 otherwise
◆ set_sumbundle_parameters()
| int ConicBundle::MatrixCBSolver::set_sumbundle_parameters | ( | const SumBundleParametersObject & | params, |
| const FunctionObject * | function = 0 |
||
| ) |
Specifies the behavior of the model (of the specified function) concerning requests to join or start a SumBundle that subsumes several models instead of providing a separate model for each funciton.
The abstract interface for these Parameters is specified in SumBundleParametersObject, a concrete implementation is SumBundleParameters. Besides the usual BundleParameters the new main parameter is specified in SumBundleParametersObject::set_acceptable_mode(), see there.
- Parameters
-
[in] params (const BundleParameters&) some update parameters for the cutting model, see e.g. ConicBundle::BundleParameters [in] function if the aggregate subgradient of a particular function is desired, provide the pointer here, otherwise this referrs to the root function (if there is only one function to be optimized over, this is this single function, otherwise it is the sum of functions)
- Returns
- 0 on success
- != 0 otherwise
◆ set_term_relprec()
| int ConicBundle::MatrixCBSolver::set_term_relprec | ( | const double | term_relprec | ) |
Sets the relative precision requirements for successful termination (default 1e-5).
- Parameters
-
[in] term_relprec (double) The algorithm stops with termination code 1, if predicted progress for the next step is less than term_relprec times absolute function value plus one.
- Returns
- 0 on success
- != 0 otherwise
◆ set_time_limit()
| void ConicBundle::MatrixCBSolver::set_time_limit | ( | CH_Matrix_Classes::Integer | time_limit | ) |
Set an upper bound on the number of seconds (user time, use negative numbers for no limit)
- Parameters
-
[in] time_limit (Integer)
- Returns
- 0 on success
- != 0 otherwise
◆ set_upper_bound()
| int ConicBundle::MatrixCBSolver::set_upper_bound | ( | int | i, |
| double | ub | ||
| ) |
Sets upper bound for variable i, use ConicBundle::CB_plus_infinity for unbounded from below.
The algorithm may have to adapt the center point aftwards. In this case the old function values will be marked as outdated and will be recomputed at the next call to e.g. solve().
- Returns
- 0 on success
- != 0 otherwise
◆ set_variable_metric()
| int ConicBundle::MatrixCBSolver::set_variable_metric | ( | int | do_variable_metric | ) |
Use a variable metric heuristic or switch off general metrics alltogether. (variable metric resets the quadratic term e.g. to some diagonal matrix, switching it off resets the quadratic term to the identity times the weight)
- Parameters
-
[in] do_variable_metric (int) - 0 switch off the scaling heuristic
- 1 use a diagonal scaling heuristic
- 2 use a diagonal scaling heuristic combined with one for the bounds
- 3 use a low rank scaling heuristic
- 4 use a low rank scaling heuristic combined with a diagonal term
- 5 use a dense scaling heuristic
- Returns
- 0 on success
- != 0 otherwise
◆ set_weight_update()
| int ConicBundle::MatrixCBSolver::set_weight_update | ( | BundleWeight * | bw | ) |
Replaces the internal update routine for choosing the weight used in the proximal term; input NULL reinstalls the default routine.
The BundleWeight class instance pointed to will be deleted on construction, i.e., ownership is passe over to the solver.
- Parameters
-
[in] bw replace internal update routine by bw, value 0 reinstalls the default routine
- Returns
- 0 on success
- != 0 otherwise
◆ solve()
| int ConicBundle::MatrixCBSolver::solve | ( | int | maxsteps = 0, |
| bool | stop_at_descent_steps = false |
||
| ) |
solves or does a prescribed number of iterations
Bundle methods solve a problem by a sequence of so called descent steps that actually bring progress by moving from the current "center point" to a new center with better objective. A descent step may consist of several function evaluations (null steps), that lead to no immediate progress but mainly improve a cutting model of the objective function close to the current center point. A minimizer to the model is accepted as descent step if the function value at this point satisfies a sufficient decrease criterion in comparison to the decrease predicted by the model. Having found a descent step, the next center is automatically shifted to this successful candidate. Termination criteria may stop the process of seeking for a descent step, in which case the current center is kept and the routine termination_code() returns the termination code.
Restarting, after each descent step, the bundle method from scratch with the new center as starting point does not endanger convergence. Therefore, a descent step is the smallest unit, after which user interaction can take place safely. To allow this there is a flag stop_at_descent_steps that will cause the code to return after the next descent step.
If you know what your are doing, you may also use the input parameter maxsteps to force the algorithm to return after at most maxsteps null steps. Calling solve again without any intermediate problem configurations will then simply continue the process where it stopped and convergence is save. During null steps one may not decrease the weight or delete nonzero variables of the center or the current candidate!
In a Lagrangean relaxation cutting plane approach one may want to separate and enlarge the dimension after a certain number of null steps. In this case the code will try to preserve the model, given appropriate subgradient extension routines have been provided. If the model cannot be extended, it has to be discarded (if subgradient extension is not successful this is done automatically), and the algorithm will be restarted from the current center point.
- Parameters
-
[in] maxsteps (int) if maxsteps>0 the code returns after at most so many null steps [in] stop_at_descent_steps (int) if true the code also returns whenever a descent step occured
- Returns
- 0 on success
- != 0 otherwise
◆ termination_code()
| int ConicBundle::MatrixCBSolver::termination_code | ( | ) | const |
Returns the termination code of the bundle algorithm for the latest descent step.
For resetting all counters relevant for termination see clear_fail_counts() .
- Returns
- 0 : Not terminated. (Continue with the next solve())
- 1 : Relative precision criterion satisfied. (See set_term_relprec())
- 2 : Timelimit exceeded. (Currently the C interface does not offer a timelimit.)
- 4 : Maximum number of function reevaluations exceeded. (Indicates that there is a problem with one of the function oracles that seems to deliver no valid upper bounds on the true function value for descent steps)
- 8 : Maximum number of quadratic subproblem failures exceeded. (Indicates that the numerical limits of the inner quadratic programming solver are reached, no further progress expected)
- 16 : maximum number of model evaluation failures exceeded (Indicates that the numerical limits of the setup of the subproblem are reached, no further progress expected)
- 32 : maximum number of failures to increase the augmented model value exceeded (Indicates that the numerical limits of the interplay between subproblem and quadratic programming solver are reached, no further progress expected)
- 64 : maximum number of oracle calls (function evaluations) exceeded, see set_eval_limit()
- 128 : maximum number of oracle failures exceeded. This refers to function evaluations that terminate with insufficient precision but still provide a new approximate subgradient. A failure typically indicates numerical difficulties with the precision requirements. (Currently the interface does not allow to manipulate the limit, it is set to 10)
The documentation for this class was generated from the following file:
 1.8.13
1.8.13